




Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра компьютерных систем и программных технологий
Отчет по лабораторной работе №12
(Учебная дисциплина «Теория автоматического управления»)
Исследование вынужденных колебаний нелинейных САУ
в Simulink
Работу выполнил студент группы №4081/2
Работу принял преподаватель___________
Санкт-Петербург
2010
1. Цель работы.
Исследование условий синхронизации автоколебательных нелинейных систем внешним гармоническим воздействием.
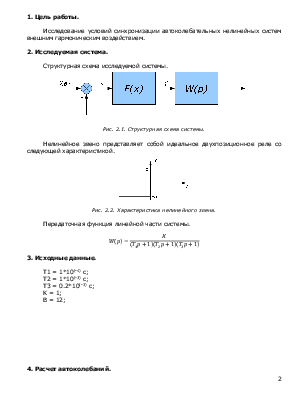
2. Исследуемая система.
Структурная схема исследуемой системы.
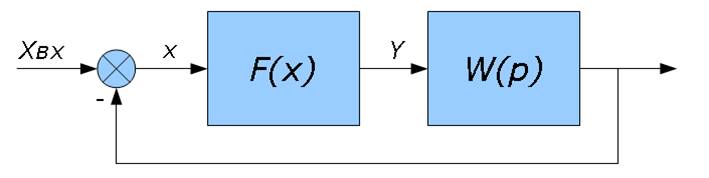
Рис. 2.1. Структурная схема системы.
Нелинейное звено представляет собой идеальное двухпозиционное реле со следующей характеристикой.
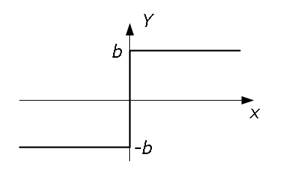
Рис. 2.2.
Характеристика нелинейного звена.
Передаточная функция линейной части системы.
![]()
3. Исходные данные.
T1 = 1*10(-4) c;
T2 = 1*10(-3) c;
T3 = 0.2*10(-3) c;
K = 1;
B = 12;
4. Расчет автоколебаний.
Автоколебания на входе нелинейного элемента имеют следующую амплитуду и частоту.
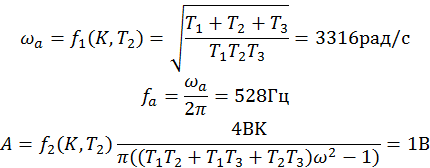
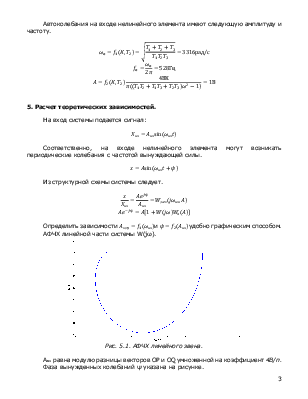
5. Расчет теоретических зависимостей.
На вход системы подается сигнал:
![]()
Соответственно, на входе нелинейного элемента могут возникать периодические колебания с частотой вынуждающей силы.
![]()
Из структурной схемы системы следует.
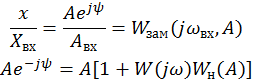
Определить
зависимости ![]() и
и
![]() удобно
графическим способом.
удобно
графическим способом.
АФЧХ линейной части системы W(jω).
 |
Aвх равна модулю разницы векторов OP и OQ умноженной на коэффициент 4B/π.
Фаза вынужденных колебаний ψ указана на рисунке.
Пороговому значению соответствует вектор PR перпендикулярный вещественной оси.
Таким образом, искомые зависимости имеют следующий вид.
![]()
![]()
Зависимости были рассчитаны и построены с помощью Matlab.
|
% ------------ Исходные данные -----------------------------B = 12; T1 = 1*10^(-3); T2 = 1*10^(-3); T3 = 0.2*10^(-3); K = 1; % ------------ Расчет автоколебаний ------------------------% Частота wa = sqrt( ( T1+T2+T3 )/( T1*T2*T3 ) ); % рад/с fa = wa/(2*pi); % Гц % Амплитуда Aa = ( 4*B*K )/( pi*( (T1*T2+T2*T3+T1*T3)*wa^2 - 1) ); % ------------ Зависимость Aвх.пор от частоты вх. сигнала --hFigure1 = figure('Color',[1 1 1]); hAxes1 = axes('Visible','on','Parent',hFigure1); box('on'); hold('all'); grid on; xlabel('\omega','FontSize',13); ylabel('A_{пор}','FontSize',13); w_in = 0.001:1:1000000; s = j*w_in; W_jw = K./( (T1*s+1).*(T2*s+1).*(T3*s+1) ); A_por = 4*B*abs(imag(W_jw))/pi; plot(w_in, A_por); xlim([0, 10000]); % ------------ Зависимость фазы вынужд колебаний от амплитуды гармонич. % -------------сигнала hFigure2 = figure('Color',[1 1 1]); hAxes2 = axes('Visible','on','Parent',hFigure2); box('on'); hold('all'); grid on; xlabel('A','FontSize',13); ylabel('\psi','FontSize',13); w = 0.5*wa; s = j*w; W_jw = K/( (T1*s+1).*(T2*s+1).*(T3*s+1) ); A_por = 4*B*abs(imag(W_jw))/pi; A = A_por:0.2:10; psi = asin(A_por./A); plot(A, psi) |
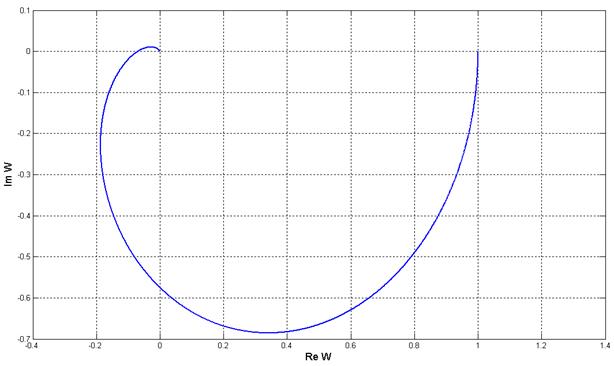
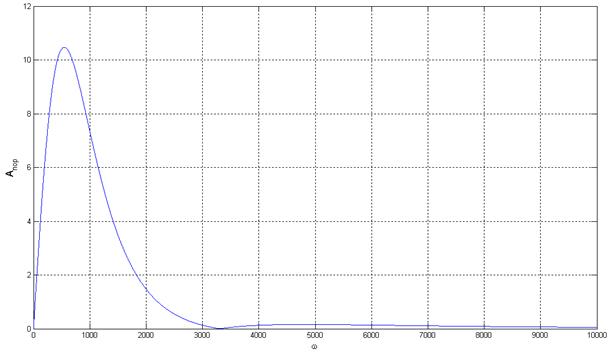
Графики зависимостей.
 |
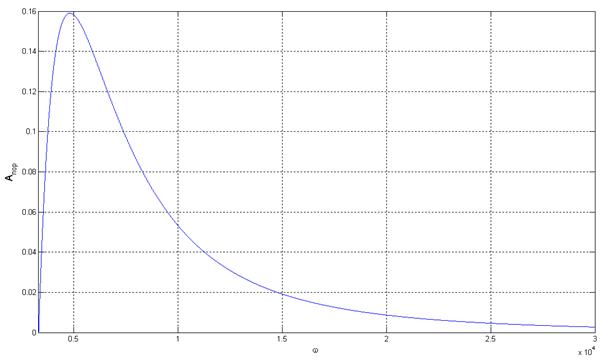 |
Рис. 5.3. Зависимость пороговой амплитуду от частоты вх.сигнала,
участок характеристики начиная с ωвх = ωа.
Ситуация когда значение пороговой амплитуды входного сигнала становится равной нулю, соответствует на рисунке 5.1. точке пересечения АФЧХ разомкнутой системы с действительной осью, мнимая часть АФЧХ равна нулю, а это как раз соответствует частоте автоколебаний.
На рисунке 5.3. изображена зависимость пороговой амплитуды входного сигнала от частоты входного сигнала при значениях частот начиная со значения частоты автоколебаний.
Зависимость фазы колебаний от амплитуды входного сигнала рассчитывается при частоте входного сигнала равной половине частоты автоколебаний. Амплитуда входного сигнала изменяется начиная от Апор, соответствующего данной частоте.
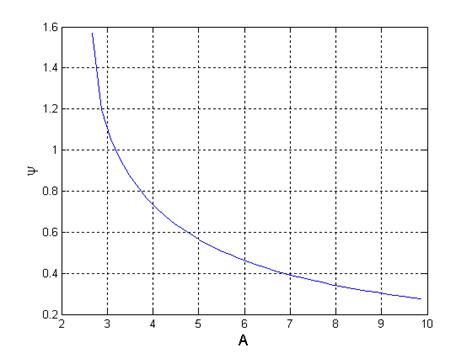
Рис. 5.4. Зависимость фазы колебаний от
амплитуды входного сигнала.
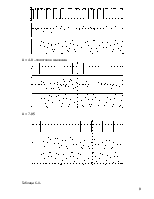
6. Моделирование вынужденных колебаний в Simulink.
Для начала необходимо проверить рассчитанные значения амплитуды и частоты автоколебаний.
Схема моделирования.
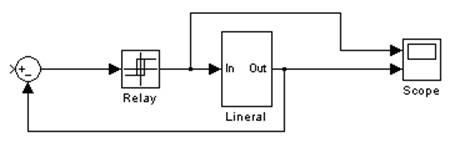
Рис. 6.1. Схема для
моделирования автоколебаний.
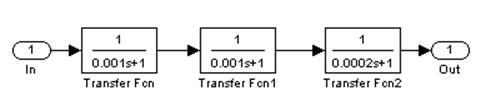
Рис. 6.2. Схема линейного
звена системы.
Снятые осциллограммы.
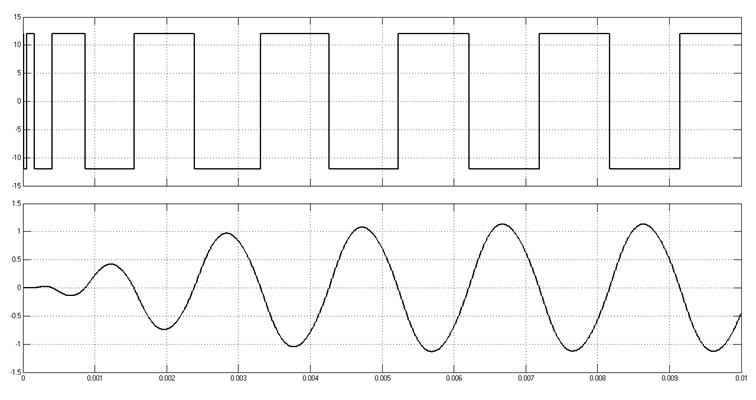
Рис. 6.3. Осциллограммы
автоколебаний.
Измеренные параметры автоколебаний:
– Амплитуда автоколебаний — 1.13;
– Период автоколебаний — приблизительно 2 мс, соответственно, частота около 500 Гц.
Снятие
зависимостей ![]() и
и
![]() .
.
Схема моделирования.
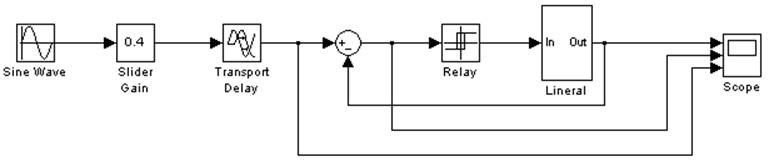
Рис. 6.4. Схема моделирования вынужденных колебаний
в Simulink.
Зависимость порогового значения амплитуды входного сигнала от частоты автоколебаний.
На выбранной частоте постепенно увеличиваем значение амплитуды входного сигнала. Величина амплитуды при которой колебания на входе нелинейного элемента принимают синусоидальную форму и имеют частоту равную частоте входного сигнала — это и есть Aпор.
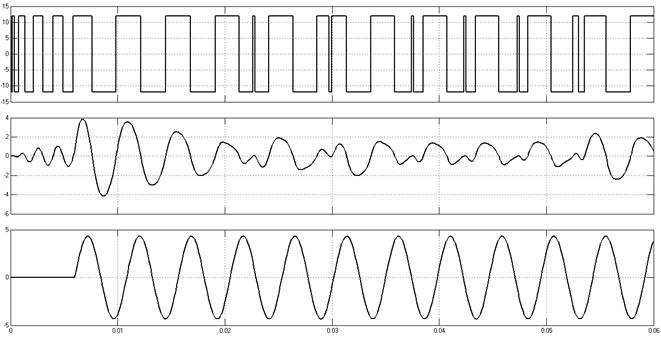
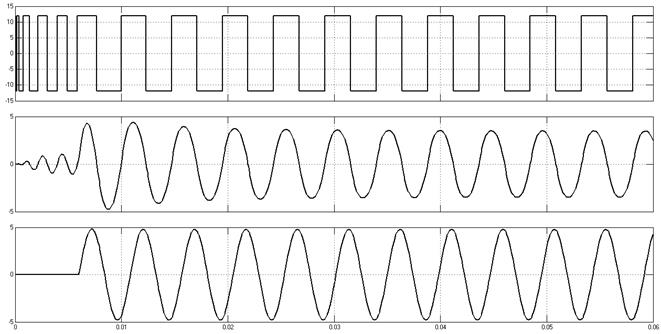
Примеры осциллограмм при различной амплитуде вынуждающего воздействия. Частота вынуждающего воздействия равна 1300 рад/с.
A = 4.34
A = 4.8 – пороговое значение.
A = 7.85
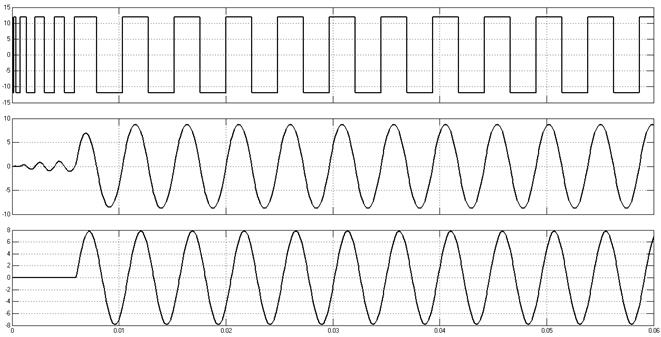
Таблица 6.1.
 |
Экспериментальный и теоретический графики снятой зависимости.
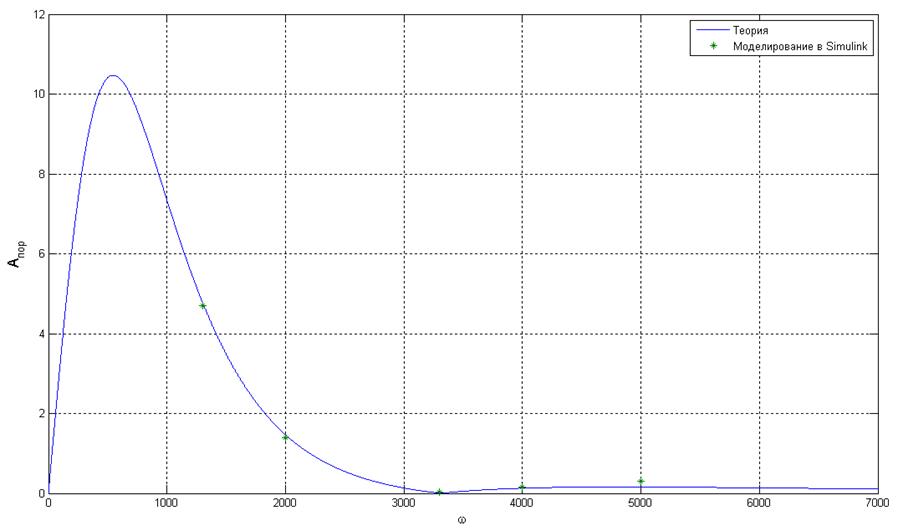
Рис. 6.4. Зависимость
пороговой амплитуду от частоты вх. сигнала.
Зависимость фазы сигнала на входе нелинейного элемента от амплитуды автоколебаний.
Таблица 6.2.
 |
Экспериментальный и теоретический графики снятой зависимости.
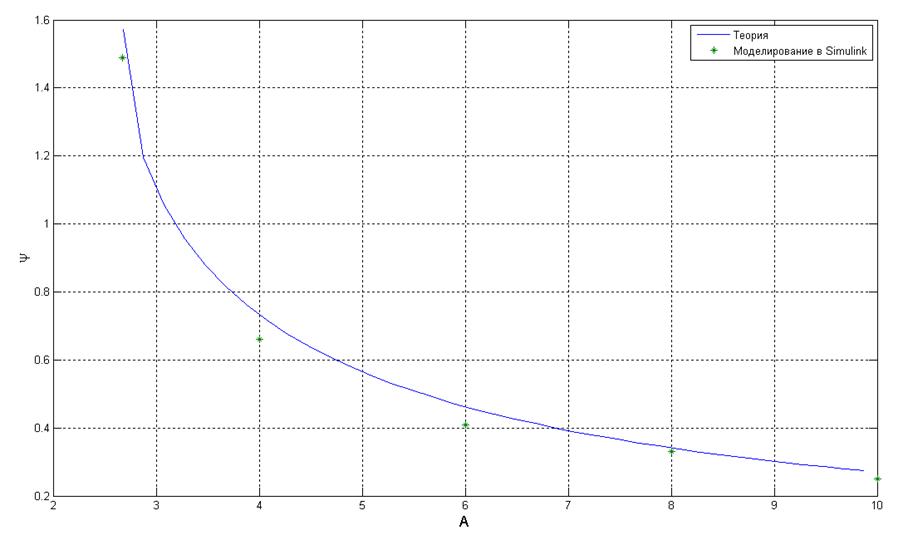
Рис. 6.5. Зависимость фазы
колебаний от
амплитуды входного сигнала.
7. Выводы и анализ результатов работы.
В работе были исследованы условия синхронизации автоколебательных нелинейных систем внешним гармоническим воздействием. Получена зависимость пороговой амплитуды, при которой происходит синхронизация от частоты входного гармонического воздействия.
Чем ближе частота внешнего гармонического сигнала к частоте автоколебаний нелинейной системы, тем необходимая для синхронизации пороговая амплитуда входного сигнала меньше.
Результаты моделирования совпали с теоретическими.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.