Исследование наблюдателя неизмеряемых координат состояния объекта (наблюдатель Люенбергера)

Факультет Технической Кибернетики

Кафедра Компьютерных Систем и Программных Технологий

Отчет

по лабораторной работе №10

Исследование наблюдателя неизмеряемых координат состояния объекта (наблюдатель Люенбергера)

Исследование компьютерных систем управления

Работу выполнили: группа 5081/10

Группа 5081/1

Преподаватель:

Подпись преподавателя:___________________

2011

Цель работы:  ознакомление с принципами построения и особенностями работы наблюдателя неизмеряемых координат состояния управляемой системы с помощью динамической модели (наблюдатель Люенбергера).

Теоретическая часть

При решении задач управления (в частности, оптимального управления) часто требуется знание всех координат состояния объекта. Но не всегда имеется возможность их измерения. Для восстановления неизмеряемых координат объекта применяются наблюдатели в форме математической модели, эквивалентной  объекту. При расхождении измеряемых координат состояния объекта  и аналогичных координат модели,  производится коррекция  координат  состояния модели. Так как  все координаты модели измеряемы,  их   и используют в качестве  полного вектора  координат состояния объекта.

Наблюдатель Люенбергера предназначен для восстановления всех координат объекта, не подвергающегося воздействию случайных помех.

Пусть объект управления описывается линейной векторно-матричной моделью вида:

где:  х – вектор координат состояния объекта, k – дискретный момент времени, измеряемых в количестве периодов квантования, T₀ = const, u – вектор управляющих воздействий, x(0) – вектор начальных условий, y – вектор выхода.

Пусть в объекте точно могут быть измерены только вектор входа u(k) и вектор выхода y(k), а все или часть «внутренних» координат состояния x(k) - не измеряемы. Включим параллельно объекту его дискретную математическую модель. Затем сравним измеряемые координаты  объекта с аналогичными координатами модели  и образуем цепь коррекции состояния модели . В результате получаем наблюдатель Льюинбергера (см. рис. 1).

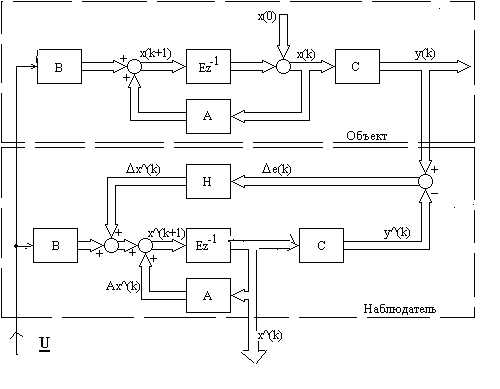
Рис. 1. Структурная схема дискретного наблюдателя Люенбергера

Основной проблемой синтеза этого наблюдателя является определение параметров цепи коррекции  - параметров матрицы H. Так как цепью коррекции связываются две динамические системы, параметры коррекции  должны, как минимум,   выбираться  из  условия  обеспечения   устойчивости получившейся сложной системы. Для синтеза  матрицы  H можно использовать метод оптимизации переходного процесса в функции  минимизации  интегрального  квадратичного критерия.

Алгоритм работы наблюдателя Люенбергера

При программной реализации алгоритма каждый раз перед началом моделирования формируются матрицы А_а, В_а, А, В на основе веденных данных.

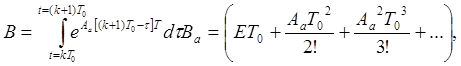
где T₀ – период квантования, А_а, В_а – параметры аналогового объекта, А, В – параметры дискретной модели объекта. Матрица С = |1 0| как для аналоговой, так и для дискретной модели объекта. Вектор начального состояния объекта х(0) = |х₀; 0|.

Алгоритм вычисления матрицы Н наблюдателя

При разработке алгоритма вычисления матрицы Н используется оптимальный в смысле минимизации ЛК-критерия метод ее синтеза.

Исходные данные:  R_b = 1, N – число итераций.

Шаг 1.

Шаг 2.

Шаг 3.

Шаг 4.

Шаг 5. Если , то перейти к шагу 2;

Шаг 6.  (вывод результата);

Шаг 7. Конец.

Алгоритм работы наблюдателя

Ввод приведенных выше исходных данных.

Шаг 1.

Шаг 2. Задать сигнал u(k) и измерить выход y(k) (для анализа работы алгоритма снимается целиком x(k)).

Шаг 3.

Шаг 4.

Шаг 5.  

Шаг 6. Если , тогда  и переход к шагу 2, иначе – вывод результата.

Шаг 7. Конец.

Экспериментальная часть

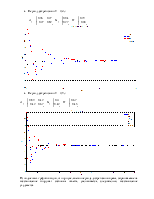
Схема лабораторной установки для исследования объекта представлена на рисунке 2.

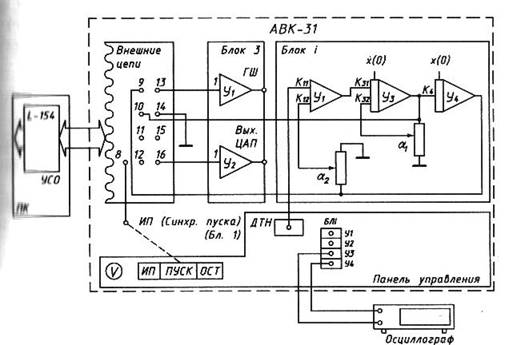
Рисунок 2. Схема лабораторной установки

Схема набора для заданных исходных данных представлена на рисунке 3.

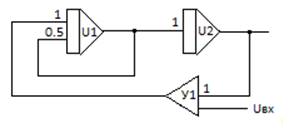
Рисунок 3. Схема набора для заданных исходных данных

Переход от скалярной формы записи исходного уравнения к векторно-матричной форме:

Исходное уравнение объекта задано линейным дифференциальным уравнением второго порядка:

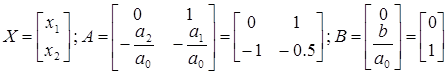
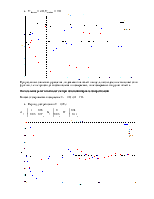
Проверка адекватности модели и объекта

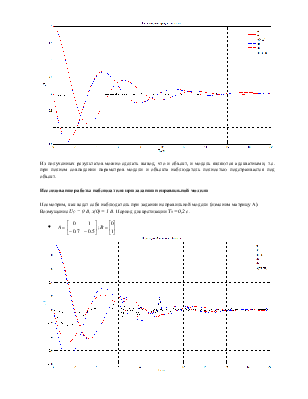
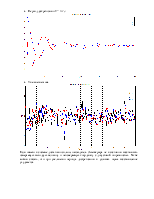
Перед началом работы необходимо убедиться в адекватности объекта и модели и определить параметры переходного процесса для них. Для этого необходимо подать на модель и объект одинаковое управляющее воздействие, одинаковые начальные условия и задать матрицы А, В,  и . В результате получены следующие значения:

Возмущение U_С  = 0 В, x(0) = 2 В. Период дискретизации T₀ = 0,1 с.

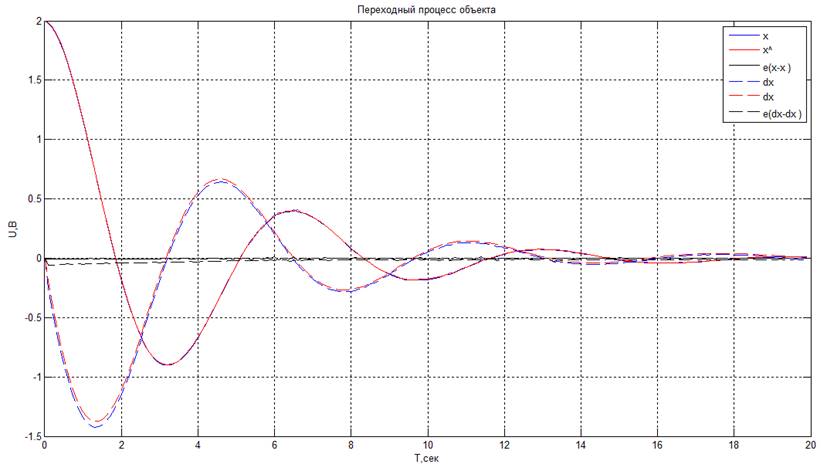
Из полученных результатов можно сделать вывод, что и объект, и модель являются адекватными, т.е. при полном совпадении параметров модели и объекта наблюдатель полностью подстраивается под объект.

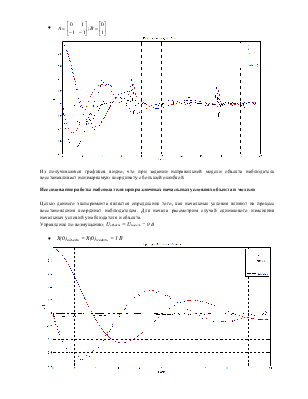
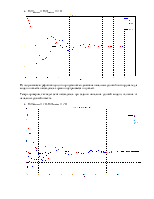
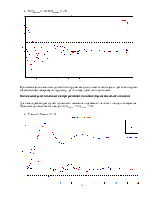
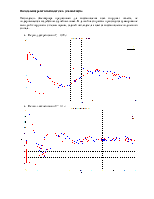
Исследование работы наблюдателя при задании неправильной модели

Посмотрим, как ведет себя наблюдатель при задании неправильной модели (изменим матрицу А).