Возмущение UС = 0 В, x(0) = 1 В. Период дискретизации T0 = 0,2 с.
·
![]()
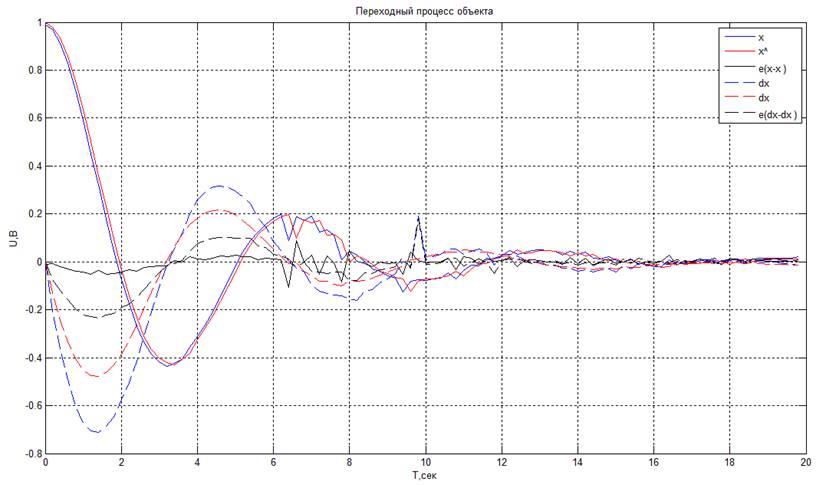
·
![]()
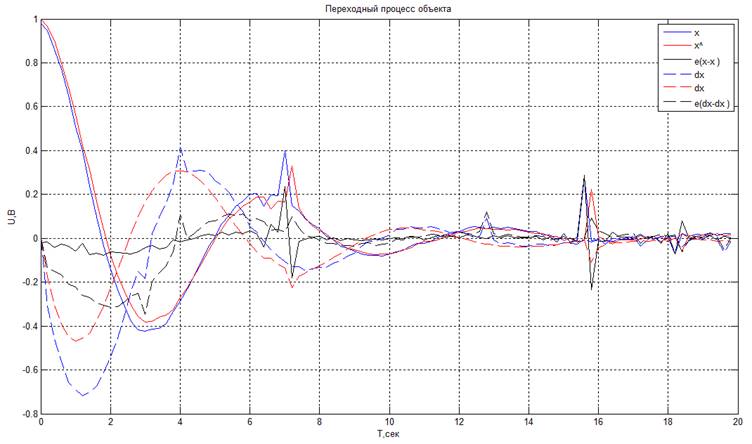
Из получившихся графиков видно, что при задании неправильной модели объекта наблюдатель восстанавливает неизмеряемую координату с большой ошибкой.
Исследование работы наблюдателя при различных начальных условиях объекта и модели
Целью данного эксперимента является определение того, как начальные условия влияют на процесс восстановления координат наблюдателем. Для начала рассмотрим случай одинакового изменения начальных условий у наблюдателя и объекта.
Управление по возмущению: Uобъект = Uмодель = 0 В
· X(0)объект = X(0)модель = 1 В
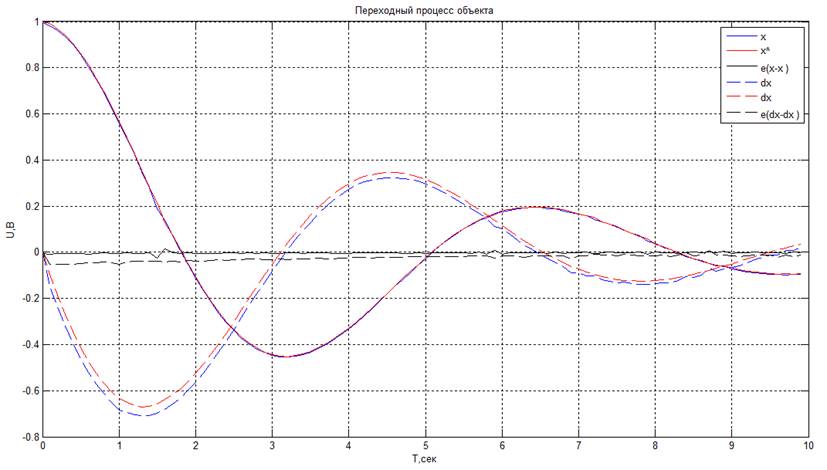
· X(0)объект = X(0)модель = 3 В

Из получившихся графиков видно, что при установке одинаковых начальных условий по координате для модели и объекта наблюдатель хорошо подстраивается под объект.
Теперь проверим, как ведет себя наблюдатель при задании начальных условий модели, отличных от начальных условий объекта.
· X(0)объект = 1 В, X(0)модель = 2 В
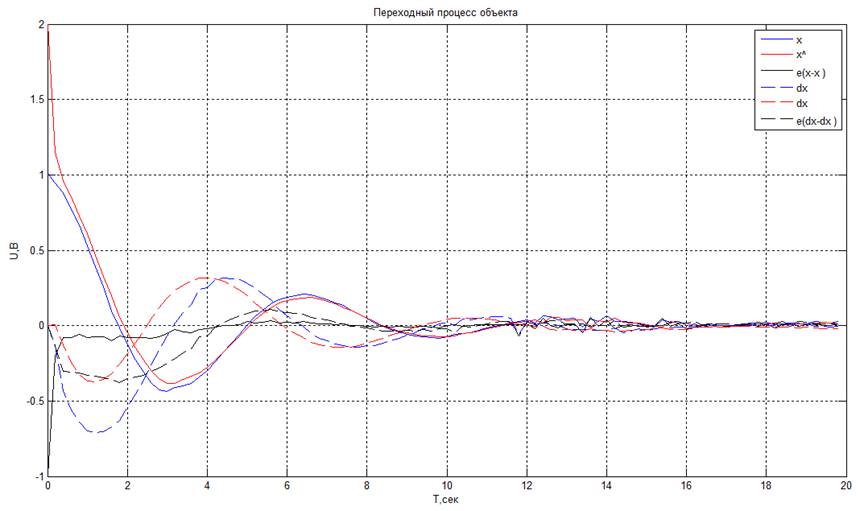
· X(0)объект = 3 В, X(0)модель = 2 В

При несовпадении начальных условий по координате модели и объекта наблюдатель достаточно хорошо восстанавливает измеряемую координату, для этого ему достаточно одного шага.
Исследование работы наблюдателя при различных значениях управления объекта и модели
Для начала рассмотрим случай одинакового изменения подаваемого на объект и модель возмущения. Начальные условия объекта и модели: X(0)объект = X(0)модель = 0 В.
· Uобъект = Uмодель = 1 В

· Uобъект = Uмодель = 2 В

При совпадении значения управления, подаваемого на объект и на модель, наблюдатель полностью восстанавливает измеряемую координату, а неизмеряемую координату восстанавливает через некоторое время.
Теперь проверим, как ведет себя наблюдатель при различных значениях управления, подаваемого на объект и на модель.
· Uобъект = 1 В, Uмодель = 2 В
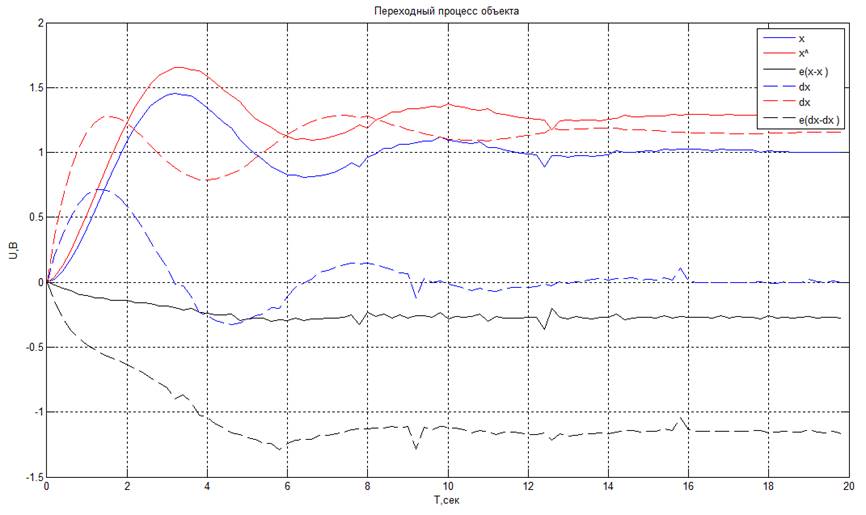
· Uобъект = 3 В, Uмодель = 0 В

При различных значениях управления, подаваемого на объект и модель, наблюдатель не выполняет свои функции, т.е. не происходит восстановления ни измеряемых, ни неизмеряемых координат объекта.
Исследование работы наблюдателя при изменении периода дискретизации
Во всех экспериментах возмущение UС = 0 В, x(0) = 1 В.
· Период дискретизации T0 = 0,05 с.
![]()
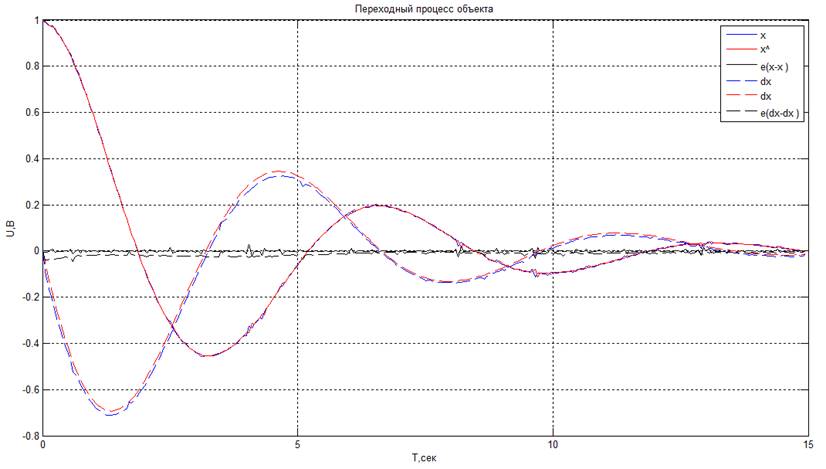
· Период дискретизации T0 = 0,3 с.
![]()

· Период дискретизации T0 = 0,5 с.
![]()

Из полученных графиков видно, что при увеличении периода дискретизации время, затрачиваемое на восстановление координат состояния объекта, увеличивается, следовательно, восстановление ухудшается.
Исследование работы наблюдателя в условиях шума
Наблюдатель Люенбергера предназначен для восстановления всех координат объекта, не подвергающегося воздействию случайных помех. В данной части работы производится суммирование выходной координаты с белым шумом, задачей наблюдателя является восстановление полученного сигнала.
· Период дискретизации T0 = 0,05 с.
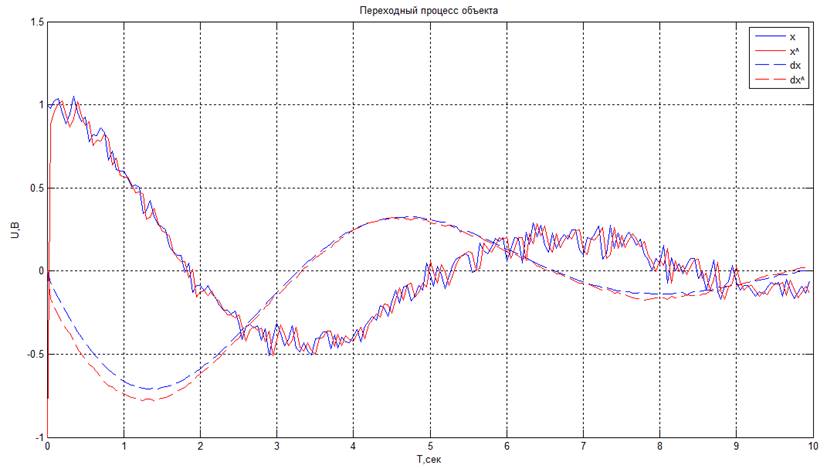
· Период дискретизации T0 = 0,1 с.
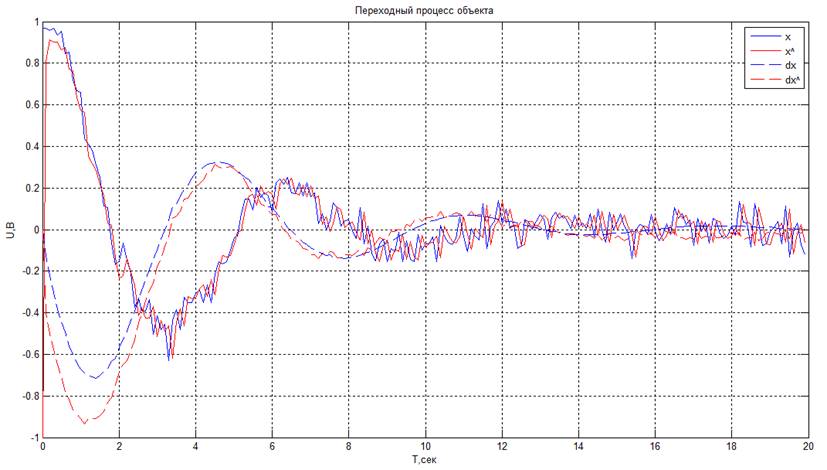
· Период дискретизации T0 = 0,3 с.
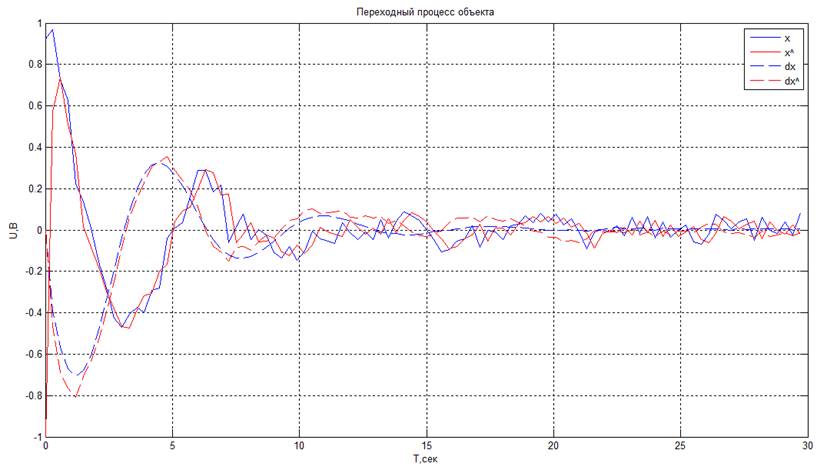
· Увеличение шума

Если помехи в системе достаточно сильны, наблюдатель Люенбергера не в состоянии восстановить измеряемую выходную величину и неизмеряемую координату с допустимой погрешностью. Также можно сказать, что при увеличении периода дискретизации в условиях шума восстановление ухудшается.
Выводы
В данной работе было проведено исследование наблюдателя неизмеряемых координат состояния управляемой системы с помощью динамической модели (наблюдатель Люенбергера).
При полном совпадении параметров модели и объекта наблюдатель полностью подстраивается под объект и восстанавливает как измеряемые, так и неизмеряемые координаты.
Если модель объекта задана неправильно, то наблюдатель восстанавливает неизмеряемую координату с большой погрешностью.
При несовпадении начальных условий объекта и модели наблюдатель быстро восстанавливает измеряемую координату, устраняя ошибку за один шаг, и долго восстанавливает неизмеряемую координату.
При различных значениях управления, подаваемого на объект и модель, наблюдатель не выполняет свои функции, т.е. не происходит восстановления ни измеряемых, ни неизмеряемых координат объекта. Это связано с тем, что у наблюдателя нет чувствительности по управлению, т.к. управление не входит в обратную связь.
При изменении периода дискретизации наблюдатель подстраивается под объект. При увеличении периода дискретизации восстановление происходит, но увеличивается время, затрачиваемое на восстановление координат состояния объекта.
В условиях помех работа наблюдателя Люенбергера затруднена. При небольших значениях помехи восстановление происходит достаточно качественно. Однако данный наблюдатель не следует применять, если помехи велики и пренебречь ими нельзя, т.к. он не выполняет свои функции в этом случае.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.