Исследование системы компьютерного управления с ПИД-регулятором. Ознакомление с практическими методами настройки промышленных систем управления

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра автоматики и вычислительной техники

ОТЧЕТ

по лабораторной работе № 5-3

Исследование системы компьютерного управления с ПИД-регулятором

Выполнил студент гр. 5081/1                                                                                 

Проверил:                                                                                                                 

Санкт-Петербург

2009

1.  Цель работы

1). ознакомление с практическими методами настройки промышленных систем управления;

2). исследование влияния параметров систем цифрового управления на качество процессов управления.

2.  Теоретические сведения

Уравнение ПИД-регулятора в непрерывной форме:

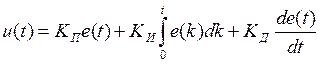, где   - рассогласование управляемой координаты и уставки (ошибка управления).

В дискретной форме уравнение можно записать в виде:          

В рекуррентной форме ПИД-закон имеет вид:

, где  

 

Т₀ – период квантования.

Начальное значение рекуррентной формы:

Изменяя коэффициенты К_П, К_ид, К_дд, можно получить рекуррентную форму для П-, И-,  Д-, ПИД- законов управления.

В данной работе проводится моделирование объекта, заданного линейным дифференциальным уравнением второго порядка вида:

где а₀, а₁, а₂, b – постоянные коэффициенты.

Исходные данные:

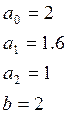
Оценка показателей качества производится по формулам:

   - перерегулирование

- колебательность

Схема набора для заданных исходных данных представлена на рис. 2.1.

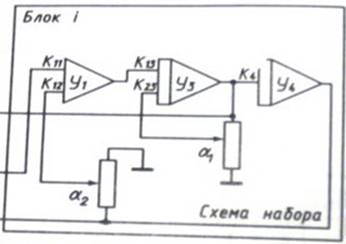
Рис. 2.1. Схема набора для заданных исходных данных.

где                                         

3.    Экспериментальная часть

3.1. Проверка адекватности объекта

Схема лабораторной установки для исследования объекта представлена на рис. 3.1.1.

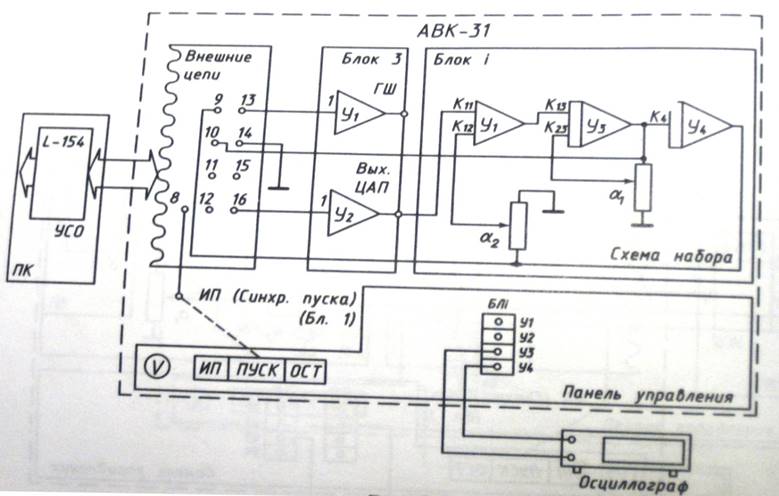
Рис. 3.1.1. Схема лабораторной установки.

Передаточная функция объекта управления:

Перед началом работы необходимо убедиться в адекватности объекта и определить параметры переходного процесса для него (время переходного процесса t_пп).

Возмущение U_С = 1 В.

Переходный процесс объекта представлен на рис. 3.1.2.

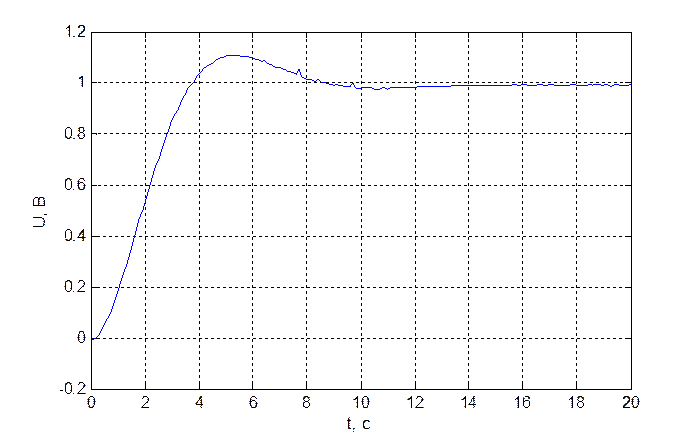
Рис. 3.1.2. Переходный процесс объекта.

Параметры переходного процесса для исследуемого объекта:

сек

3.2. Исследование влияния пропорциональной составляющей на переходную характеристику системы

Передаточная функция регулятора:

Передаточная функция объекта управления:

Структурная схема исследуемой системы представлена на рис. 3.2.1.

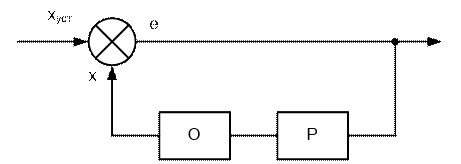
Рис. 3.2.1. Структурная схема исследуемой системы.

Передаточная функция замкнутой системы:

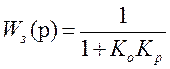, К_о = 1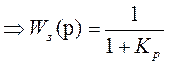

Переходная характеристика системы при х_уст=2В  и различных значениях параметра К_п представлена на рис. 3.2.2.

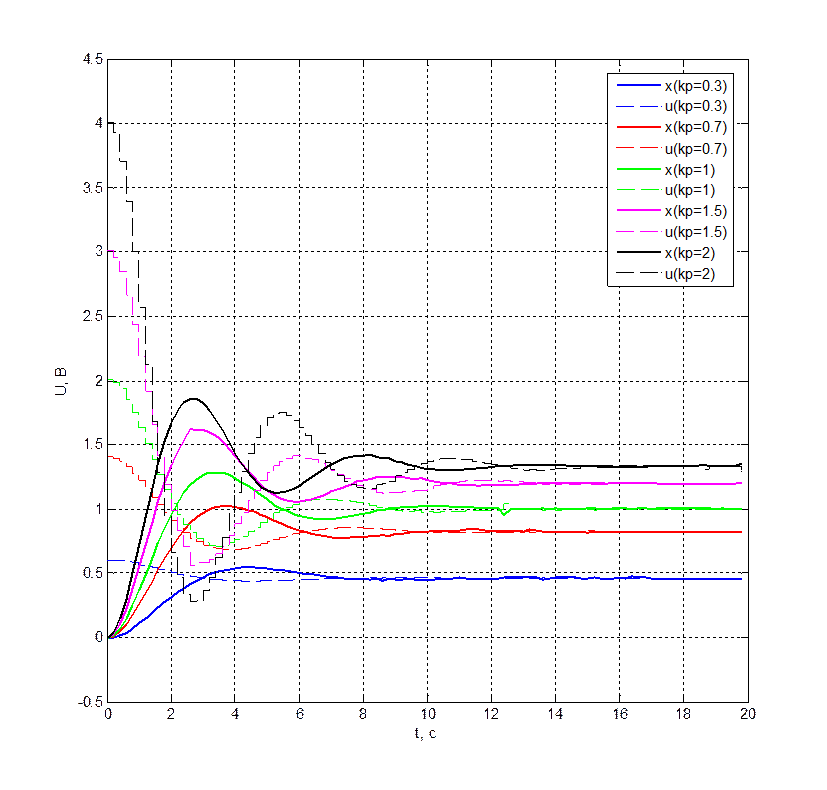
Рис. 3.2.2. Переходная характеристика системы при  различных K_п

( x_уст = 2 В, N = 100, T = 200 мс ).

В данном случае:

K_п = 0.3:

Время переходного процесса:     7 с

Перерегулирование: 

K_п = 0.7:

                         8,5 с

                             

K_п = 1:

                                     9,5 с

                                

K_п = 1.5:

                           10,5 с

                         

K_п = 2:

                           11,5 с

                              

Таблица 3.2.1. Значения показателей качества и величины статической ошибки при различных значениях K_п.

Из полученных результатов можно сделать вывод, что при увеличении К_п   величина статической ошибки уменьшается, однако при этом увеличивается колебательность системы и время переходного процесса.

3.3. Исследование влияния интегральной составляющей на переходную характеристику системы

Постараемся улучшить качество переходного процесса, добавив в систему И-составляющую.

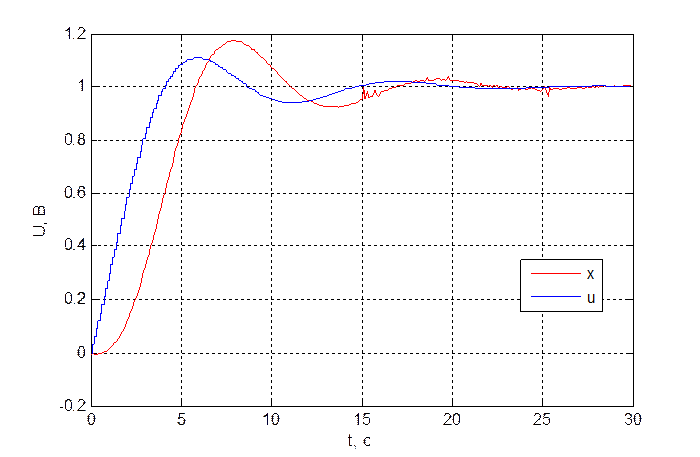
Рис. 3.3.1. Переходная характеристика системы при К_и = 0.3, x_уст  = 1 В, N = 300 , T = 100 мс.

 20 с                                  

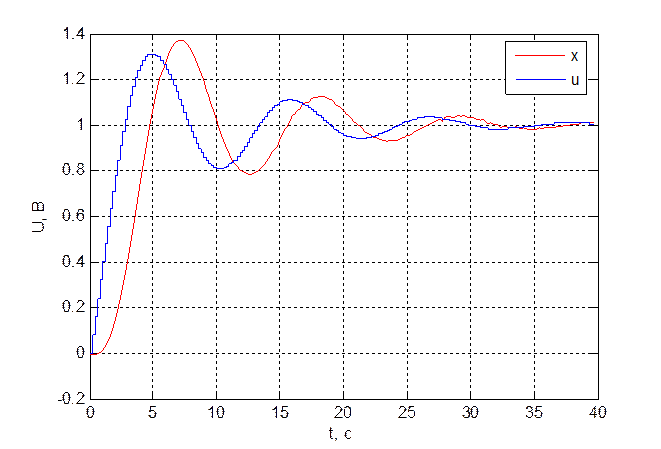
Рис. 3.3.2. Переходная характеристика системы при К_и = 0.4, x_уст  = 1 В, N = 200 , T = 200 мс.