Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Компьютерных Систем и Программных Технологий
ОТЧЕТ
по лабораторной работе №5.2
«Исследование системы компьютерного управления с ПИД-регулятором»
по предмету «Компьютерные системы управления»
Работу выполнили студент группы 5081/1
студентка группы 5081/10
Преподаватель ____________
Санкт-Петербург
2011
1. Цель работы
Исследовать систему с ПИ-регулятором в замкнутом состоянии; рассмотреть проблемы устойчивости компьютерных систем управления с ПИ-регулятором.
2. Методика исследования
Передаточная
функция объекта: ![]()
Постоянная
времени объекта: ![]()
Коэффициент
передачи объекта: ![]()
Объект
первого порядка описывается дифференциальным уравнением: ![]()
Условия устойчивости для объекта первого порядка, охваченного обратной связью ПИ-регулятора:
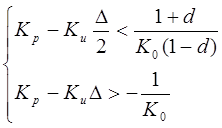
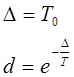
3. Исходные данные
а0 = 1 а1 = 0.5
b = 1
![]() ,
, ![]()
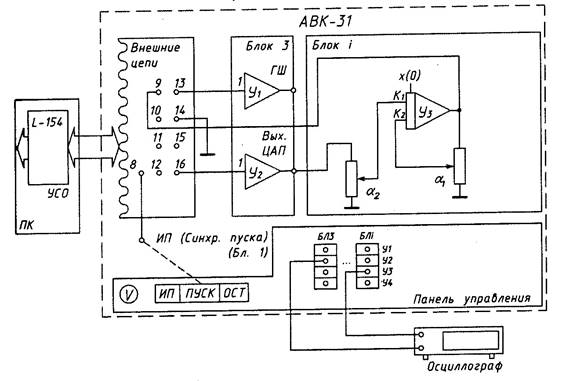
Рис.1. Схема исследования
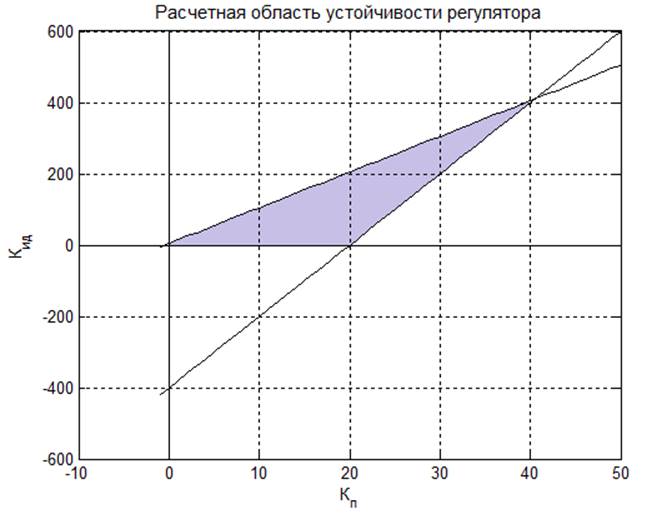
Рис.2. Теоретическая область устойчивости регулятора для T=0.1 c
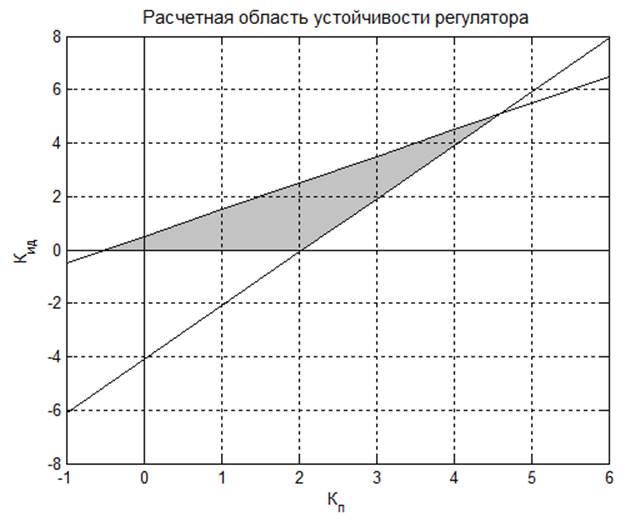
Рис.3. Теоретическая область устойчивости регулятора для T=1 c
4. Экспериментальное исследование
Для проведения экспериментального исследования найдем точки пересечения теоретических прямых с осями координат и для каждой из этих точек (исключая отрицательное пересечение с осью KИД, т.к. оно лежит за пределами области устойчивости) снимем три графика: для значений коэффициентов, лежащих внутри теоретической области устойчивости; на границе теоретической области устойчивости; вне теоретической области устойчивости. После этого сравним полученные данные с теоретическими и сделаем выводы.
Для всех случаев в параметрах регулятора было выставлено значение уставки, равное 1.
4.1. T=0.1 c
N1(-0.5;0)
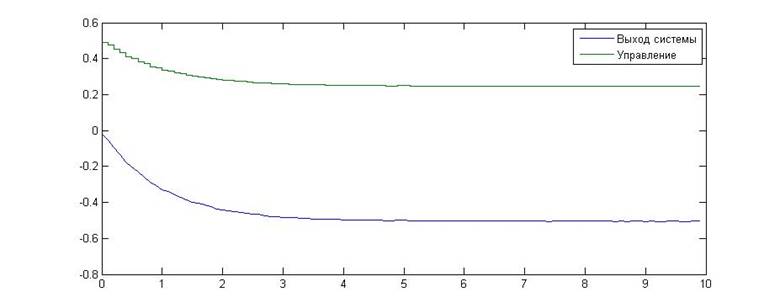
Рис.5. Зависимость значения сигнала от времени для KП=0.5, KИ=0
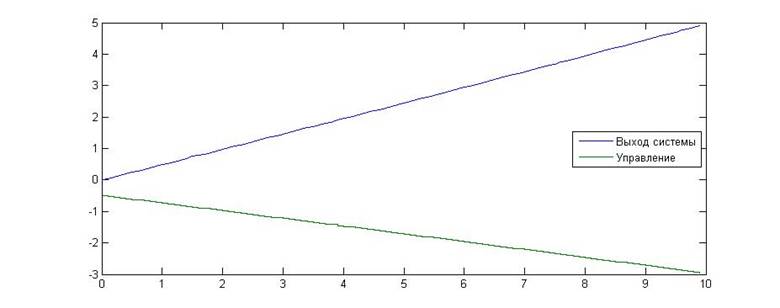
Рис.6. Зависимость значения сигнала от времени для KП=-0.5, KИ=0
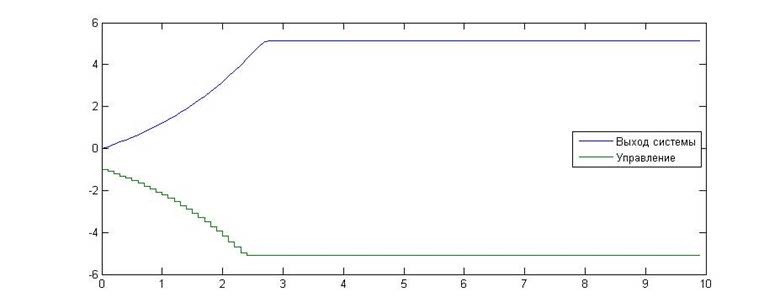
Рис.7. Зависимость значения сигнала от времени для KП=-1, KИ=0
Как видно из приведенных графиков, в данном случае расчетные данные совпали с теоретическими. На границе устойчивости выходной сигнал системы линейно возрастает, а после ее пересечения начинает увеличиваться по экспоненте, что указывает на линейный характер границы устойчивости.
N2(0;5)
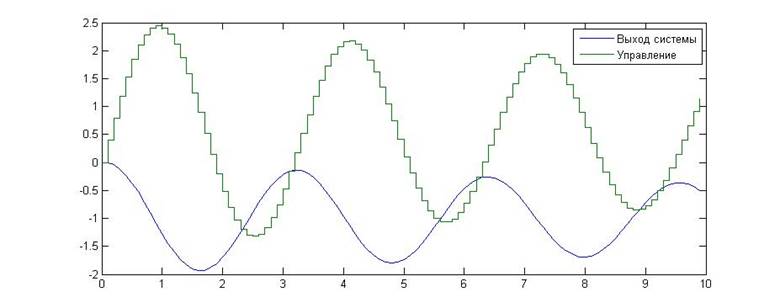
Рис.8. Зависимость значения сигнала от времени для KП=0, KИ=4
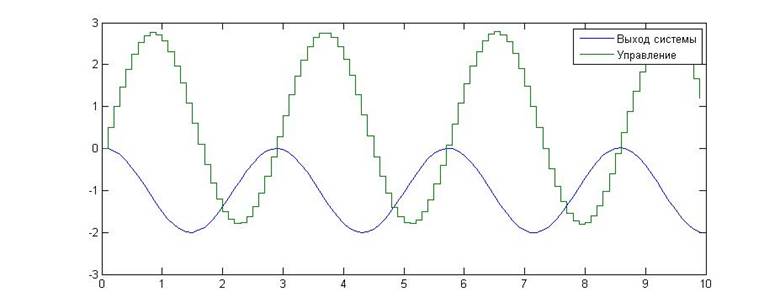
Рис.9. Зависимость значения сигнала от времени для KП=0, KИ=5
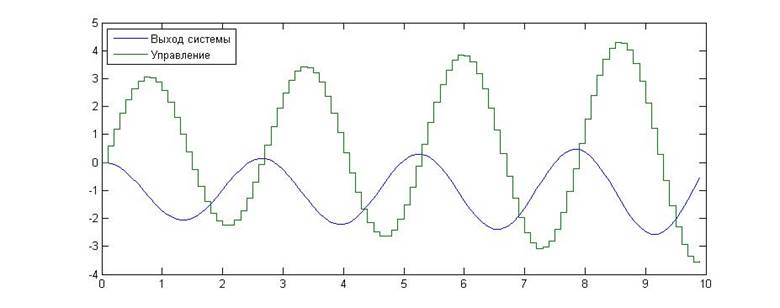
Рис.10. Зависимость значения сигнала от времени для KП=0, KИ=6
Как видно из приведенных графиков, в данном случае результаты экспериментальных исследований совпали с теорией. При приближении к границе устойчивости в системе начинают появляться затухающие колебания, превращающиеся в автоколебания а границе устойчивости и в незатухающие колебания вне границы устойчивости . Из этих наблюдений можно сделать вывод о том, что данная граница является колебательной.
N3(20;0)
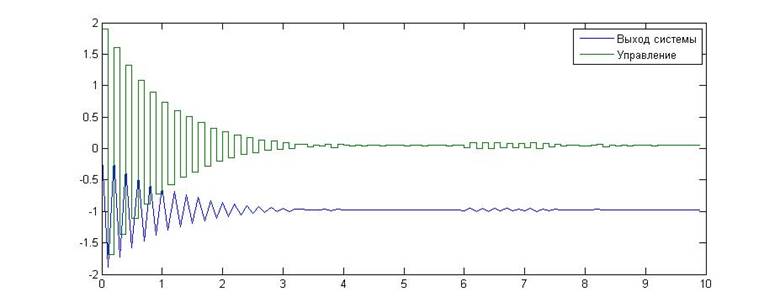
Рис.11. Зависимость значения сигнала от времени для KП=19, KИ=0
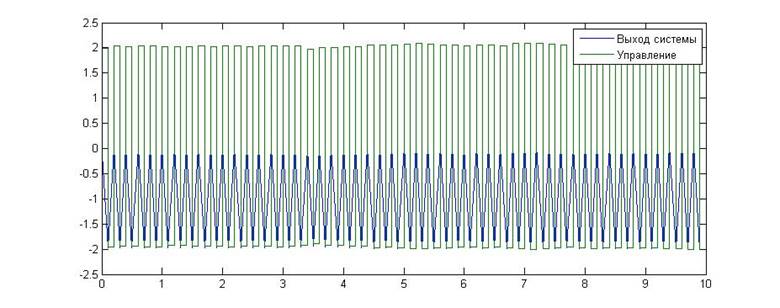
Рис.12. Зависимость значения сигнала от времени для KП=20, KИ=0
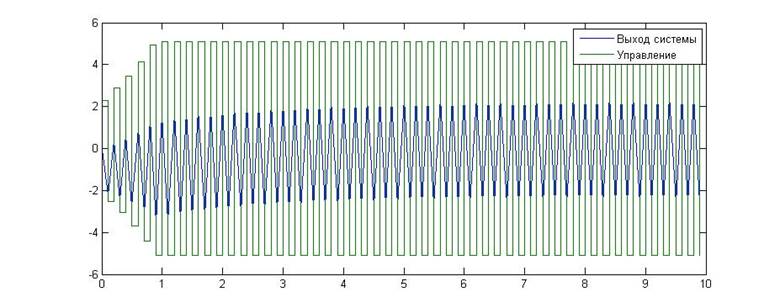
Рис.13. Зависимость значения сигнала от времени для KП=21, KИ=0
Как видно из приведенных графиков, в данном случае экспериментальное исследование подтвердило теоретические расчеты. Данная граница является колебательной. На последнем графике (при значениях коэффициентов, не лежащих в области устойчивости) амплитуда колебаний фиксируется на некотором значении. Это связано с тем, что сигнал управления упирается в ограничения, заданные для данного регулятора, и не может возрастать дальше.
4.2. T=1 c
N1(-0.5;0)
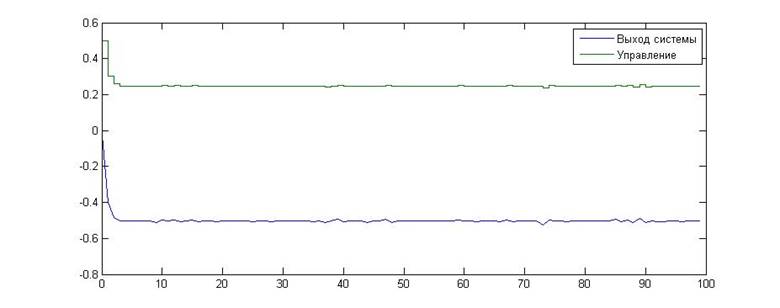
Рис.14. Зависимость значения сигнала от времени для KП=0.5, KИ=0
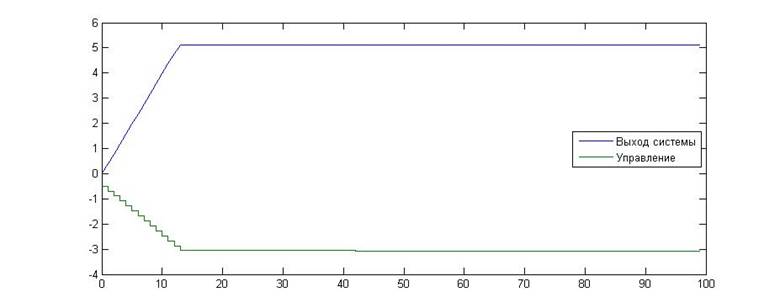
Рис.15. Зависимость значения сигнала от времени для KП=-0.5, KИ=0
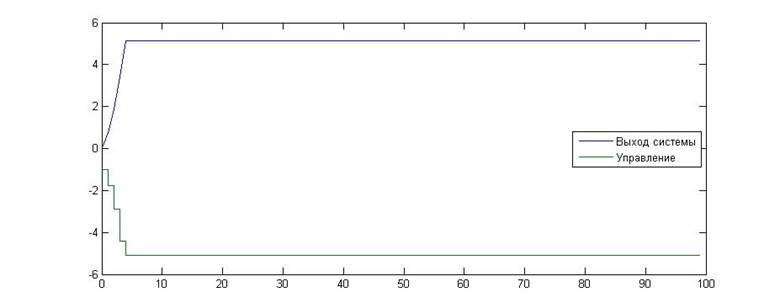
Рис.16. Зависимость значения сигнала от времени для KП=-1, KИ=0
Как видно из приведенных графиков, в данном случае экспериментальное исследование подтвердило расчеты. Данная граница является линейной границей устойчивости.
N2(0;0.5)
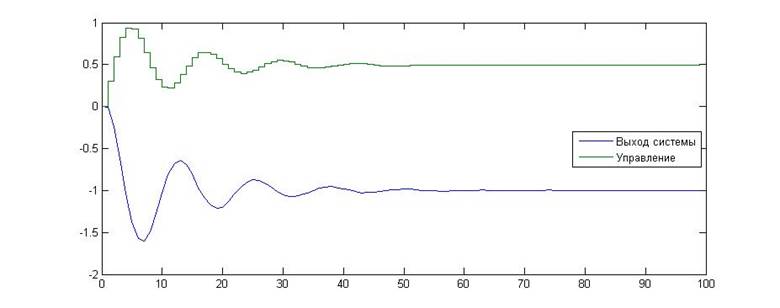
Рис.17. Зависимость значения сигнала от времени для KП=0, KИ=0.3
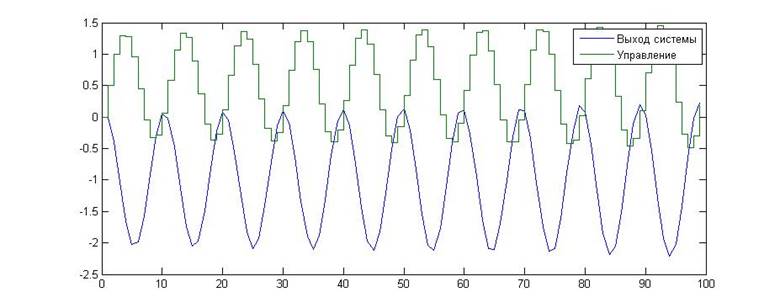
Рис.18. Зависимость значения сигнала от времени для KП=0, KИ=0.5
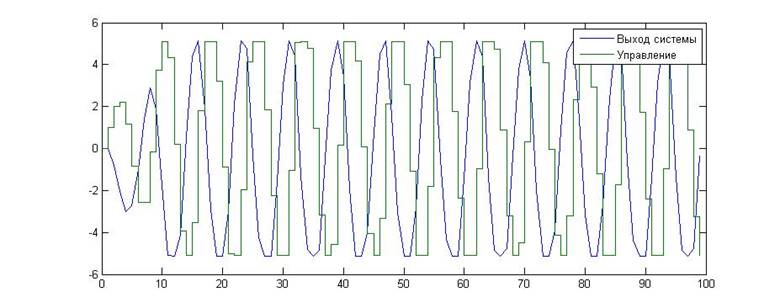
Рис.19. Зависимость значения сигнала от времени для KП=0, KИ=1
Как видно из приведенных графиков, в данном случае экспериментальное исследование подтвердило теоретические расчеты. Данная граница является колебательной.
N3(2;0)
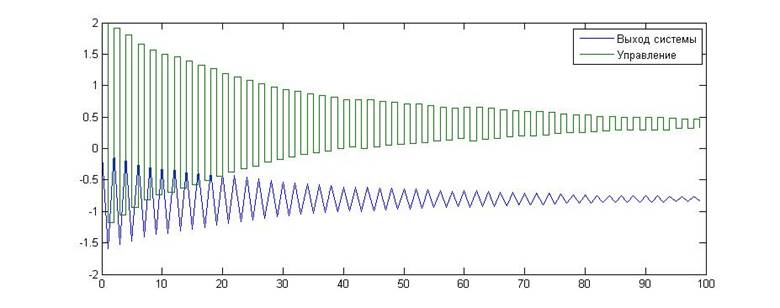
Рис.20. Зависимость значения сигнала от времени для KП=2, KИ=0
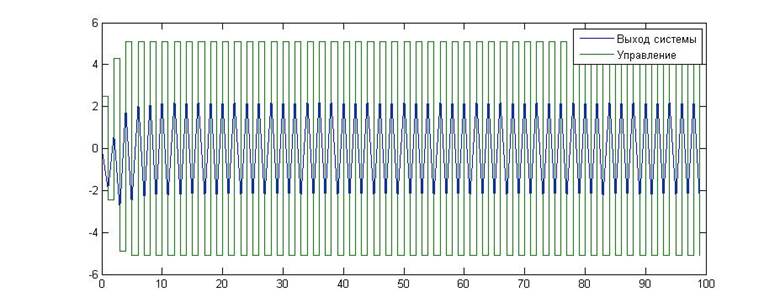
Рис.21. Зависимость значения сигнала от времени для KП=2.5, KИ=0
Как видно из приведенных графиков, в данном случае результаты эксперимента несколько расходятся с расчетными данными. Так, точка (2;0), которая, по расчетым данным, должна являться границей устойчивости, на деле лежит внутри границы. однако точка (2.5;0) уже лежит вне границы устойчивости, что указывает на малое расхождение теории и эксперимента.
5. Выводы
В ходе проведения данной лабораторной работы было проведено исследование областей устойчивости ПИ-регулятора для различных значений периода квантования. По результатам работы можно сделать вывод о том, что ПИД-регуляторы не всегда позволяют получить требуемое качество управления. Для каждого регулятора существует область устойчивости, зависящая от параметров системы, в которую включен регулятор. При выходе значений коэффициентов регулятора за пределы области устойчивости мы получаем неустойчивую систему, использование которой может привести к непредсказуемым последствиям.
Границы области устойчивости бывают двух видов: линейные и колебательные. При пересечении линейной границы значение сигнала на выходе системы начинает экспоненциально возрастать; при пересечении колебательной же системы на выходе системы появляются расходящиеся колебания (как правило, однако, ограниченные допустимой величиной управляющего сигнала для данного ПИД-регулятора).
Следует также отметить, что уже при приближении к границам устойчивости выходной сигнал системы начинал изменять свое поведение. Поэтому в тех случаях, когда вид сигнала критичен, разумно будет держать значения коэффициентов регулятора в центре области устойчивости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.