Исследование оптимальной системы ЛК-управления с наблюдателем Люенбергера и наблюдателем Калмана

Лабораторная работа №12: Исследование оптимальной системы ЛК-управления с наблюдателем Люенбергера

1.  Цель работы

Изучение структуры построения и особенностей работы оптимальной системы ЛК-управления с наблюдателем Люенбергера;

Оценка эффективности применения наблюдателя в оптимальной системе ЛК-управления по начальным условиям;

2.  Теоретические положения

Как известно, оптимальное управление линейным объектом с использованием квадратичного критерия оптимальности (ЛК-управление) осуществляется в форме пропорционального управления по всем координатам состояния объекта.

Если часть координат не может быть измерена, то при синтезе оптимального ЛК-управления применяются специальные восстановители (наблюдатели) неизмеряемых координат состояния в форме специальных корректирующих динамических моделей. Структурная схема таких систем  при управлении по начальным представлена на рис.1.1.

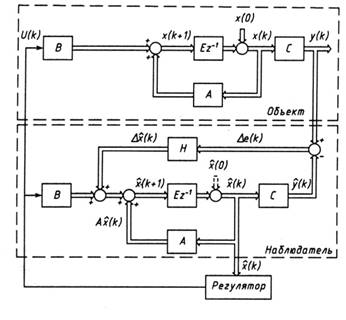
Рис 1.1. Структурная схема системы ЛК-управления по начальным условиям

Уравнение управляемого объекта

,       x(0) = x0  0;

где  – вектор координат состояния объекта; u(k)  – вектор измеряемых координат состояния объекта, , , .

Уравнение наблюдателя

Так как в системах ЛК-управления наблюдатель строится по типу динамической системы, математически подобной объекту, с возможностью корректировки координат состояния модели, то его динамика может быть описана в дискретном времени следующей системой алгебраических уравнений:

Уравнение регулятора

3.  Исходные данные

В настоящей работе рассматривается объект, математическая модель которого - дифференциальное уравнение второго порядка.

               

a₀ = 1             a₁ = 1           a₂ = 2           b = 2

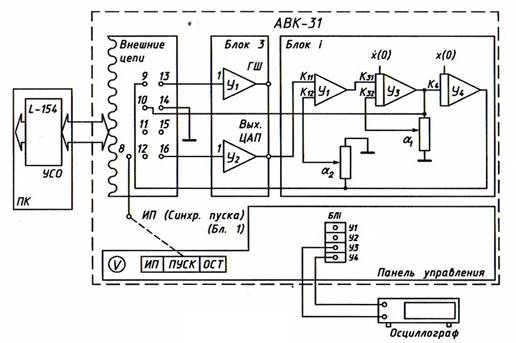
Рис. 3.1. Схема набора

Тогда дифференциальное уравнение системы имеет вид:

Параметры непрерывной модели

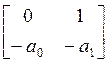Х =          А==              В==

4.  ВЫполнение работы

4.1  Исследование системы ЛК-управления с полностью измеряемыми координатами состояния объекта

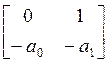Х =          А==              В==

Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= 

Q =     .

k1 = 0.365424          

k2 = 0.642245

J = 127.8913

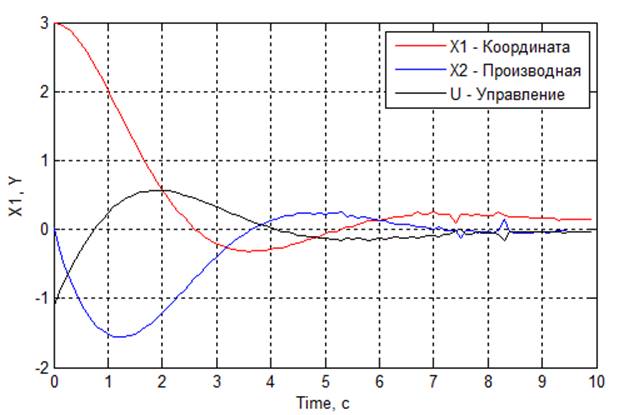
Рис 4.1. Графики переходных процессов

4.2  Исследование системы ЛК-управления с не полностью измеряемыми координатами состояния объекта

Оценка чистого запаздывания и фиксация переходного процесса при одинаковых значениях начальных условий в объекте и наблюдателе

Параметры дискретной модели (начальные условия модели и объекта заданы одинаково):

Т₀ = 0.1с     А_д =     В_д =     X0= 

Q =     .

k1 = 0.365424          

k2 = 0.642245

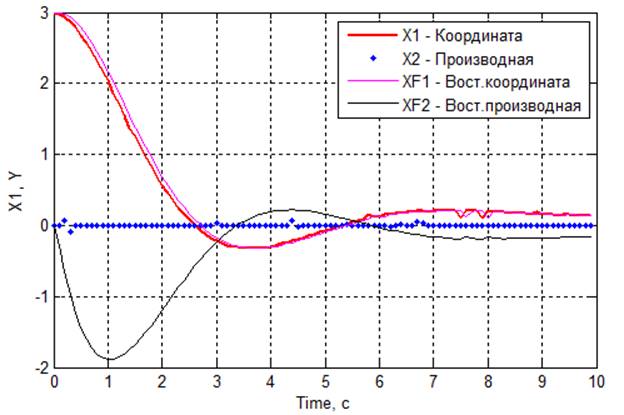
Рис 4.2. Графики переходных процессов

Оценка влияния инерционного запаздывания и получение соответствующих характеристик переходного процесса

Параметры дискретной модели (начальные условия модели и объекта различны):

Т₀ = 0.1с     А_д =     В_д =     X0= 

Q =     .

k1 = 0.365424          

k2 = 0.642245

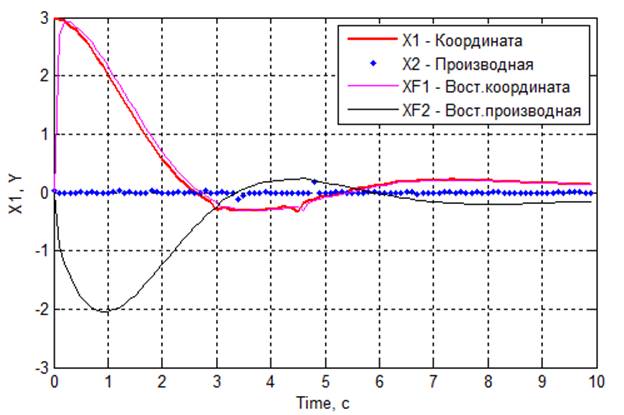
Рис 4.3. Графики переходных процессов

4.3  Исследование квазиоптимальной системы ЛК-управления c шумом и без.

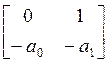Х =          А==              В==

Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= 

Q =     .

k1 = 0.365424          

k2 = 0.642245

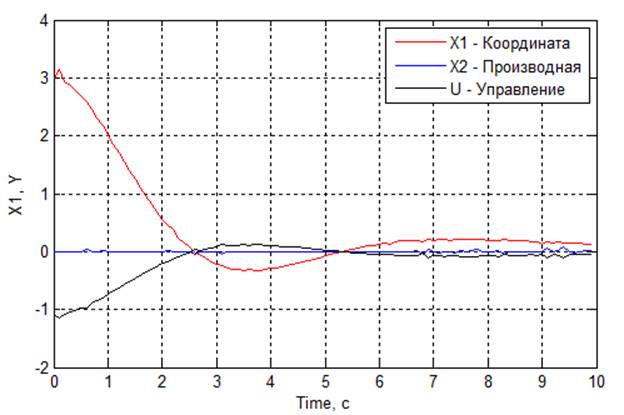
J1 = 159.5739, J2 = 189.2100, J3 = 205,3211

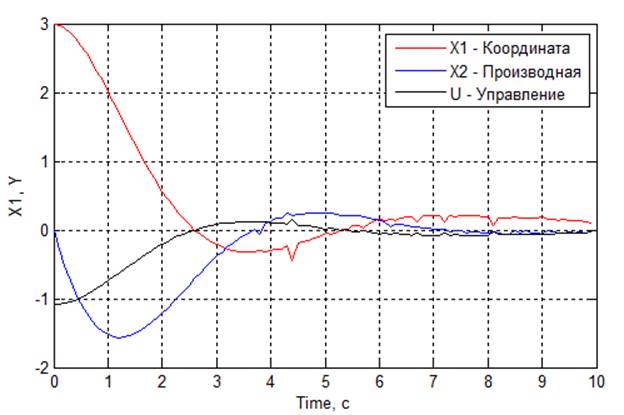
Рис 4.4. Графики переходных процессов