Исследование оптимальной системы ЛК-управления с наблюдателем Люенбергера и наблюдателем Калмана, страница 2

Рис 4.5. Графики переходных процессов

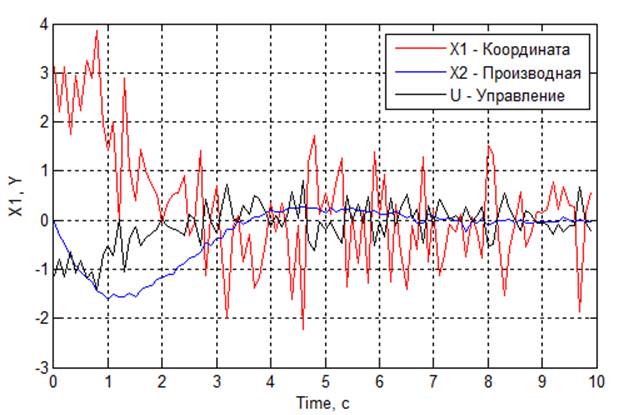
Рис 4.6. Графики переходных процессов

Лабораторная работа №13: Исследование оптимальной системы ЛК-управления с наблюдателем Калмана

1.  Цель работы

Изучение организации, методов синтеза и исследование особенностей работы оптимальной системы линейно-квадратичного управления (ЛК-управления) с наблюдателем Калмана.

2.  Теоретические положения

Как известно, организация систем оптимального терминального управления с использованием квадратичного критерия оптимальности (ЛК-управление) требует знания всех координат состояния объекта.

Если часть координат не может быть измерена, то при синтезе оптимального ЛК-управления применяются специальные восстановители (наблюдатели) неизмеряемых координат состояния. Если объект и измеритель координат находятся под воздействием случайных помех, в качестве наблюдателя наибольшее распространение получил фильтр Калмана. Структурная схема системы оптимального терминального ЛК-управления с фильтром Калмана в качестве наблюдателя представлена на рис.2.1.

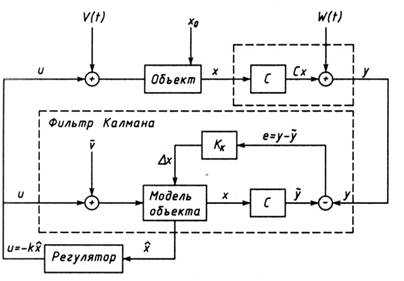
Рис.2.1. Структурная схема системы ЛК-управления с фильтром Калмана

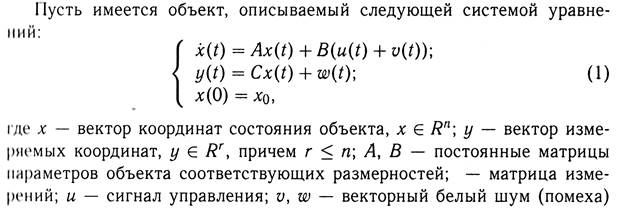
Описанные выше процессы восстановления координат состояния и формируемые на их основе сигналы обратной связи иллюстрируются структурной схемой, приведенной на рис. 2.2.

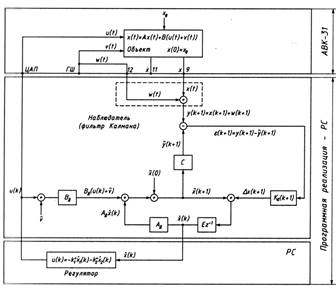
Рис.2.2. Структурная схема системы ЛК-управления с фильтром Калмана

3.  Исходные данные

В настоящей работе рассматривается объект, математическая модель которого - дифференциальное уравнение второго порядка.

               

a₀ = 1             a₁ = 1           a₂ = 2           b = 2

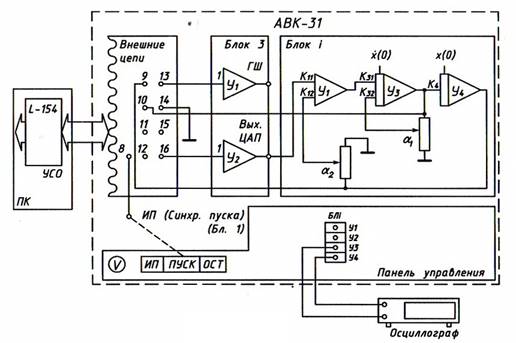
Рис. 3.1. Схема набора

Тогда дифференциальное уравнение системы имеет вид:

Параметры непрерывной модели

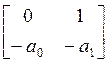Х =          А==              В==

4.  ВЫполнение работы

4.1  Первый этап

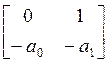Х =          А==              В==

Параметры дискретной модели:

Т₀ = 0.1с     А_д =     В_д =     X0= 

Q =     .

В последующих пунктах параметры дискретных моделей одинаковы

k1 = 0

k2 = 0

J = 140.3587

Мат. ожидание помехи = 0.44

Дисперсия помехи входа(dv) = 0.72

Дисперсия помехи измерения(dw) = 0.72

Рис 4.1. Графики переходных процессов

4.2  При заданных начальных условиях x₀, и разомкнутой обратной связи (k1 = 0, k2 = 0)

k1 = 0

k2 = 0

J = 147.5397

Рис 4.2. Графики переходных процессов

4.3  При заданных начальных условиях x₀ и замкнутой обратной связи (k1 0, k2  0)

J = 143.2839

Рис 4.3. Графики переходных процессов

4.4  Оценить эффективность введения наблюдателя в систему оптимального управления  k1 0, k2 = 0 (При управлении по одной координате)

J = 151.5631

 

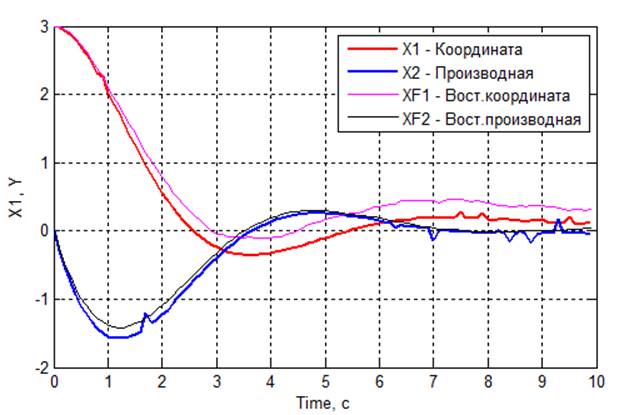
Рис 4.4. Графики переходных процессов

5.  ВЫВОДЫ

Лабораторная работа №12: Исследование оптимальной системы ЛК-управления с наблюдателем Люенбергера

Проанализировав результаты экспериментов, можно сделать вывод о том, что несоответствие начальных условий в модели и в объекте приводит к увеличению инерционного запаздывания. При ЛК-управлении желательно использовать обе измеряемые координаты, тк при управлении по одной координате ухудшается динамика процесса, об этом свидетельствует увеличение критерия для системы с не полностью измеряемыми координатами. Шум в канале измерения так же негативно сказывается на качестве процесса.

Лабораторная работа №13: Исследование оптимальной системы ЛК-управления с наблюдателем Калмана

Сделав выводы по результатам экспериментов можно говорить о том, что качество процессов системы с наблюдателем в разомкнутом виде хуже, чем в замкнутом, так же негативно сказывается и отсутствие управления по одной из координат. Если сравнивать систему оптимального управления с наблюдателем и без, то можно сделать вывод о том, что добавление наблюдателя не всегда даёт улучшение в динамике управления, а в некоторых случаях даже ухудшает.