Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра автоматики и вычислительной техники
Дисциплина: компьютерные системы управления
Тема: Синтез и исследование оптимальной системы ЛК-управления
в дискретном времени
Выполнил студент гр. 5081/1
Проверил:
Санкт-Петербург
2009
1. Цель работы
– практическое знакомство с методикой синтеза и организацией оптимальной системы терминального управления в дискретном времени с квадратичным критерием качества;
– исследование её работы в условиях полунатурных испытаний.
2. Теоретические сведения
Описание алгоритма вычисления оптимальных коэффициентов регулятора
Пусть объект управления описывается линейным векторно-матричным уравнением вида:
![]()
где: х – вектор координат состояния объекта,
k – дискретный момент времени, измеряемых в количестве периодов квантования T0 = const,
u – вектор управления,
x(0) – вектор начальных условий.
Необходимо синтезировать обратную связь (регулятор), обеспечивающую формирование управления, которое осуществляет перевод объекта из некоторого начального состояния x(t0)¹0 в заданное конечное состояние x(N)=0 и минимизацию квадратичного критерия качества вида
![]() ,
,
где S и Q – симметричные соответственно неотрицательно определенные матрицы, а
R - симметричная и положительно определённая ненулевая диагональная матрица.
Указанный критерий является аналогом интегрального квадратичного критерия качества, используемого при синтезе непрерывных систем оптимального управления.
Для решения задачи ЛК-оптимизации в дискретном времени воспользуемся методом математического программирования.
Этот метод оптимизации основан на использовании принципа оптимизации Беллмана, который можно сформировать следующим образом: «Оптимальная стратегия управления обладает тем свойством, что каким бы ни было начальное состояние или начальное решение, последующее решение должно быть оптимальным по отношению к состоянию, возникшему в результате первого решения».
Этот принцип реализует т.н. концепцию инвариантного вложения, при использовании которой решение сложной исходной проблемы заменяется решением некоторого количества аналогичных более простых проблем. При этом решение реализуется в виде многошагового процесса последовательного решения одношаговых процессов оптимизации. В данном случае для реализации оптимального управления свободным движением системы из исходного ненулевого начального состояния в нулевое конечное состояние многошаговый процесс решения начинают с последнего участка, координаты которого известны.
В общем случае для каждого из участков траектории можно получить следующие рекуррентные формулы для вычисления оптимальных коэффициентов – KN-j, воспомогательной матрицы PN-j, управления u(N-j), критерия оптимальности JN-j.
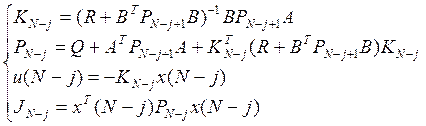
при j=1, PN=Q.
при j=N, ![]()
Полученные значения K* используются для построения оптимальной системы:
![]()
3. Экспериментальная часть
3.1. Переход от скалярной формы записи исходного уравнения к векторно-матричной форме
Уравнение объекта задано линейным дифференциальным уравнением второго порядка:
![]()
где а0, а1, а2, b – постоянные коэффициенты.
Исходные данные:
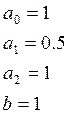
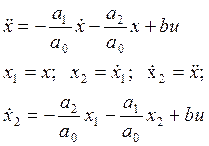
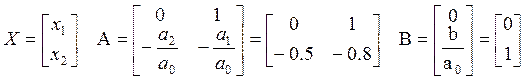
![]()
Схема набора для заданных исходных данных представлена на рис. 3.1.
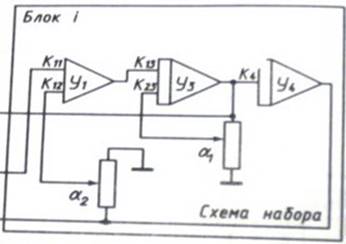
Рис. 3.1. Схема набора для заданных исходных данных.
где ![]()
![]()
![]()
4. Исследование объекта
4.1. Исследование разомкнутой системы (без регулятора)
Схема лабораторной установки для исследования объекта представлена на рис. 4.1.1.
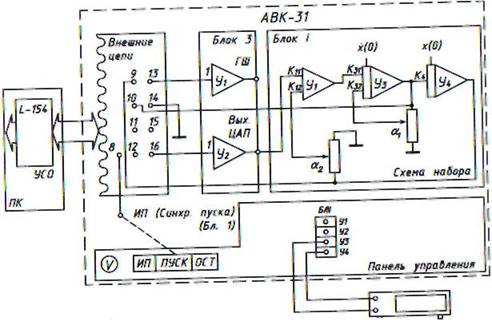
Рис. 4.1.1. Схема лабораторной установки.
Передаточная функция объекта управления:
![]()
![]()
Для проверки адекватности объекта и для сравнения с оптимальной системой, проведём исследование объекта без регулятора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.