Синтез и исследование оптимальной системы ЛК-управления. Практическое знакомство с методикой синтеза и организацией оптимальной системы терминального управления в дискретном времени с квадратичным критерием качества, страница 2

На рис. 4.1.2. приведён переходный процесс из = 1 В в = 0 В.

Время переходного процесса составило примерно 12 с, максимальное отклонение 0.1 В.

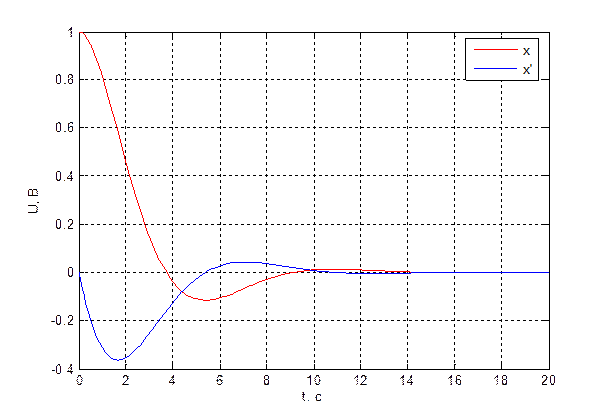
Рис. 4.1.2. Переходный процесс разомкнутой системы.

4.2. Исследование оптимальной системы при различных матрицах весовых коэффициентов критерия оптимальности Q и R

Обозначим Q = qE.

Расчет коэффициентов обратной связи и тестирование осуществлялись при начальных условиях X₀=[1; 0]^T при периоде дискретизации T₀ = 100мс.

Таблица 4.2.1

№	q	R	tпп, сек	коэффициенты ОС		критерий оптимальности
				K1	K2	Jтеор	Jэкспер
1	0,2	1	7	0,160	0,275	3,361	3,4939
2	0,5	1	6,5	0,340	0,544	8,072	8,5848
3	1	1	6	0,568	0,849	15,449	16,6873
4	2	1	5	0,901	1,259	29,320	32,2866
5	3	1	4,5	1,155	1,555	42,581	47,2298
6	5	1	4	1,548	1,998	68,151	75,1932
7	1	0,5	5,6	0,901	1,259	14,660	16,1004
8	1	2	7,5	0,340	0,544	16,144	17,1441
9	1	5	8,1	0,160	0,275	16,803	17,4476

4.3. Проверка синтезированной системы на оптимальность

Для проверки системы на оптимальность варьируем коэффициенты обратной связи системы. Рассмотрим систему для Q=E, R=E, X₀=[1; 0]^T

 

Таблица 4.1.2.

Как следует из приведенной таблицы, оптимальной системе соответствую иные значения коэффициентов обратной связи.

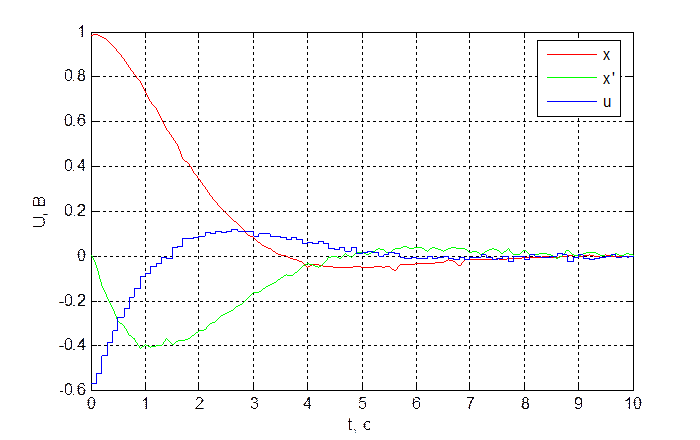
Рис. 4.3.1. Переходный процесс в оптимальной системе (Q = E, R = 1).

4.4. Исследование зависимости оптимальных коэффициентов ОС от отношения параметров критерия J Q/R и R/Q

Рис. 4.4.1. Переходные процессы системы при различных отношениях Q/R.

Рис. 4.4.2. Переходные процессы системы при различных отношениях R/Q.

На рис. 4.4.1 и 4.4.2 представлены переходные процессы () при разном отношении весов критерия J Q/R и R/Q. Из рисунков видно, что рассчитанные коэффициенты ОС соответствуют требованиям, предъявляемым к системе: при увеличении веса координат по отношению к весу управления колебательность уменьшается, вместе с ней и время переходного процесса, при этом управление, напротив, ухудшается.

При увеличении веса управления по отношению к весу координат колебательность увеличивается, вместе с ней и время переходного процесса, при этом управление, напротив, улучшается.

5. Выводы

В ходе выполнения настоящей работы было произведено исследование средств синтеза оптимальных систем.

Во-первых, было продемонстрировано улучшение временных параметров переходного процесса при использовании полученных коэффициентов обратной связи. Так если время переходного процесса разомкнутой системы (рис. 4.1.2) составляет 12 с, то при использовании корректирующей ОС оно равняется 6 с.

В пункте 4.3 было показано, что истинные оптимальные коэффициенты ОС отличаются от расчетных. Это связано с тем, что параметры реальной системы отличаются от заложенных при расчете коэффициентов ОС.