Синтез и исследование оптимальной системы ЛК-управления в непрерывном времени. Изучение методики синтеза системы оптимального терминального управления в непрерывном времени с интегральным квадратичным критерием качества, а также исследование работы системы

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра автоматики и вычислительной техники

ОТЧЕТ по лабораторной работе № 8

Дисциплина: компьютерные системы управления

Тема: Синтез и исследование оптимальной системы ЛК-управления в непрерывном времени

Выполнил студент гр. 5081/1                                                                                 

Проверил:                                                                                                                 

Санкт-Петербург

2009

1.  Цель работы

Изучение методики синтеза системы оптимального терминального управления в непрерывном времени с интегральным квадратичным критерием качества, а также исследование работы системы.

2.  Теоретические сведения

Описание алгоритма вычисления оптимальных коэффициентов обратной связи

В основу синтеза оптимальной ОС в данной работе положен метод итерационного решения нелинейного матричного уравнения Риккати путём сведения его к матричному линейному уравнению Ляпунова. Пусть имеется многомерный линейный стационарный объект, описываемый векторно-матричным уравнением вида:  

 (1)

Необходимо синтезировать управление, обеспечивающее перевод объекта из некоторого начального состояния  в заданное конечное  и минимизацию целевого функционала вида

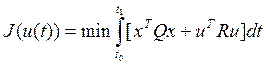, (2)

где Q и R – симметричные неотрицательно определённые диагональные матрицы. В теории управления эта задача известна как линейно-квадратичная (ЛК) проблема оптимального управления. Её решение позволяет определить параметры ОС (регуляторов), обеспечивающей наилучшие процессы в смысле минимального значения функционала (2).

Уравнение Риккати:

, (3)

где S – квадратная положительно определённая симметричная матрица. В результате находится оптимальная матрица S* и матрицы оптимальных коэффициентов ОС K*:

  (4)

Оптимальное управление формируется в виде:

, (5)

т.е. в форме пропорциональной ОС по всем координатам вектора состояния. Требуется решить нелинейную векторно-матричную систему вида:

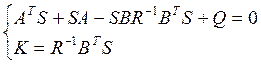 (6)

Решение системы (6) можно получить итерационным способом, предварительно преобразовав её к линейной форме.

 

 (7)

Если предполагать, что  и  известны, то полученное уравнение (7) является линейным относительно S и может быть решено итерационным способом.

Начальные значения коэффициентов K должны выбираться из условия обеспечения устойчивости замкнутой системы. Для этого в уравнение (7) необходимо ввести параметры замкнутой системы управления. Уравнение (1) перепишем в виде: 

 

где  - матрица параметров замкнутой системы.

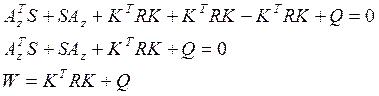
В результате полученное уравнение преобразуется к уравнению Ляпунова:

Решение уравнения Ляпунова методом прямого интегрирования

Решение уравнения Ляпунова для устойчивой матрицы  имеет вид:

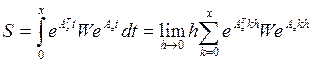 (8)

Численное решение уравнения (8) требует вычисления матричных экспонент, которые могут быть аппроксимированы следующим образом:

 

При выборе h > 0 матрица  является неособенной и всегда существует.

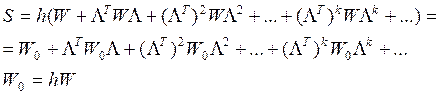  (9)

Если частные суммы из (9) обозначить как , то рекуррентную форму вычисления S можно представить следующим образом:

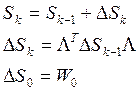  (10)

Значение h рекомендуется выбирать из условия:

где  - доминирующее собственное значение матрицы .

Описанный метод численного решения уравнения Ляпунова (10) позволяет сформулировать алгоритм решения уравнения Риккати и определить матрицу оптимальных коэффициентов ОС, реализующих условия минимизации интегрального квадратичного критерия (2).

3.    Экспериментальная часть

3.1. Переход от скалярной формы записи исходного уравнения к векторно-матричной форме

Уравнение объекта задано линейным дифференциальным уравнением второго порядка:

где а₀, а₁, а₂, b – постоянные коэффициенты.

Исходные данные:  

 

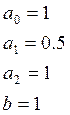
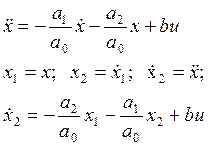
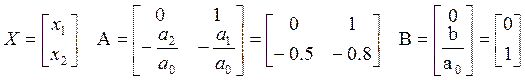
Схема набора для заданных исходных данных представлена на рис. 3.1.

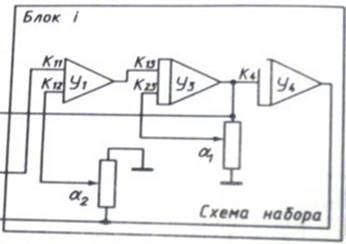
Рис. 3.1. Схема набора для заданных исходных данных.

где                                           

3.2. Определение оптимальных коэффициентов ОС

С помощью программы cal_ric2.exe были получены коэффициенты ОС. При начальных условиях:

Матрица Q:

1.00   0.00

0.00   1.00

Скаляр R:

1.00

Начальные коэффициенты ОС K1, K2:

1.00   1.00

В таблице 3.2 приведены значения оптимальных коэффициентов в зависимости от x₀.

 

Таблица 3.2. Значения оптимальных коэффициентов при варьировании н.у.

x0, В	K1	K2	J
1	0.61808	0.89594	299.9125
3	0.61808	0.89594	2699.9834

Очевидно, что значения оптимальных коэффициентов не зависят от начальных условий.

3.2.1. Зависимость оптимальных коэффициентов ОС от отношения параметров

критерия J Q/R

В таблице 3.2.1 приведены значения оптимальных коэффициентов ОС в зависимости от отношения параметров критерия J Q/R (отношение веса координат к весу управления). В таблице в столбце Q приведено значение диагональных элементов.