Синтез и исследование оптимальной системы ЛК-управления в непрерывном времени. Изучение методики синтеза системы оптимального терминального управления в непрерывном времени с интегральным квадратичным критерием качества, а также исследование работы системы, страница 2

Таблица 3.2.1. Значения оптимальных коэффициентов при варьировании Q/R.

Q	R	Q/R	K1	K2	Jтеор	Jпракт
0.2	1	0.2	0.17427	0.30318	3.4236	3.5040
0.5	1	0.5	0.37846	0.61512	8.1853	8.6791
1	1	1	0.65379	15.7162	15.7162	16.8927
2	1	2	1.09928	1.61596	30.0367	32.6856
3	1	3	1.48773	2.14983	43.9426	47.7729
5	1	5	2.24171	3.23290	71.5668	77.4340

Значение критерия важно только при сравнении качества управления при одних и тех же условиях и заданных весовых коэффициентах управления и координаты критерия. Изменяя коэффициенты ОС, получаем различные кривые переходного процесса, площадь под которыми стремимся уменьшить (засчёт уменьшения времени процесса и перерегулирования), поэтому минимум критерия даёт оптимальные коэффициенты ОС. При различных требованиях к координате и управлению, которые задаются весами критерия J, получаем различные переходные процессы, сравнивать которые по величине критерия бессмысленно. Ниже, во второй части экспериментальной программы, будет видно, как влияет отношение весов критерия на вид переходного процесса оптимальной системы.

3.2.2. Зависимость оптимальных коэффициентов ОС от отношения параметров

критерия J R/Q

В таблице 3.2.2 представлены  значения оптимальных коэффициентов при изменении отношения веса управления к весу координат критерия J.

Таблица 3.2.2. Значения оптимальных коэффициентов при варьировании R/Q.

R	Q	R/Q	K1	K2	Jтеор	Jпракт
0.5	1	0.5	1.09923	1.61554	15.0320	16,2852
1	1	1	0.65379	1.00557	15.7162	16.8927
2	1	2	0.37852	0.61504	16.3758	17.2431
5	1	5	0.17370	0.30244	17.0639	17.5058

4. Исследование объекта

4.1. Исследование разомкнутой системы (без регулятора)

Схема лабораторной установки для исследования объекта представлена на рис. 4.1.1.

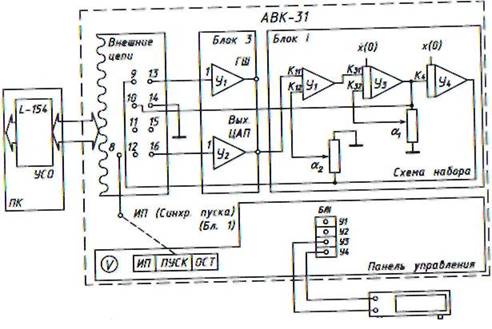
Рис. 4.1.1. Схема лабораторной установки.

Передаточная функция объекта управления:

Для проверки адекватности объекта и для сравнения с оптимальной системой, проведём исследование объекта без регулятора.

На рис. 4.1.2. приведён переходный процесс из = 1 В в = 0 В.

Время переходного процесса составило примерно 12 с, максимальное отклонение 0.1В.

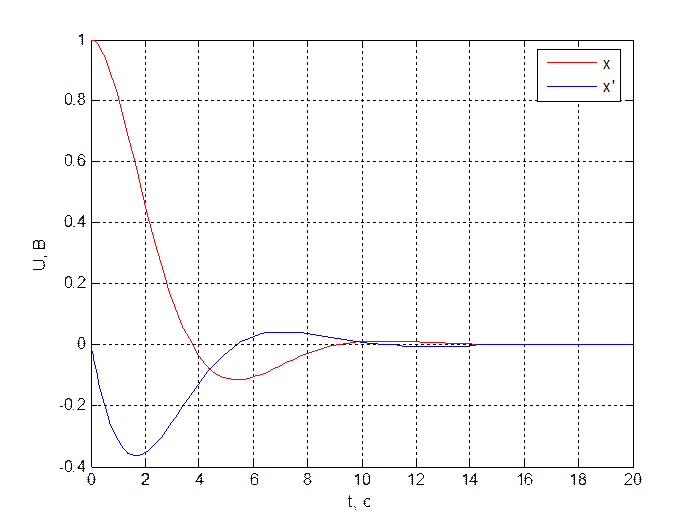
Рис.4.1.2. Переходный процесс разомкнутой системы.

4.2. Исследование зависимости оптимальных коэффициентов ОС от отношения параметров критерия J Q/R

На рис. 4.2.1 и 4.2.2 представлены переходные процессы () при разном отношении весов критерия J Q/R. Из рисунка видно, что рассчитанные коэффициенты ОС соответствуют требованиям, предъявляемым к системе: при увеличении веса координат по отношению к весу управления колебательность уменьшается, вместе с ней и время переходного процесса, при этом управление, напротив, ухудшается. 

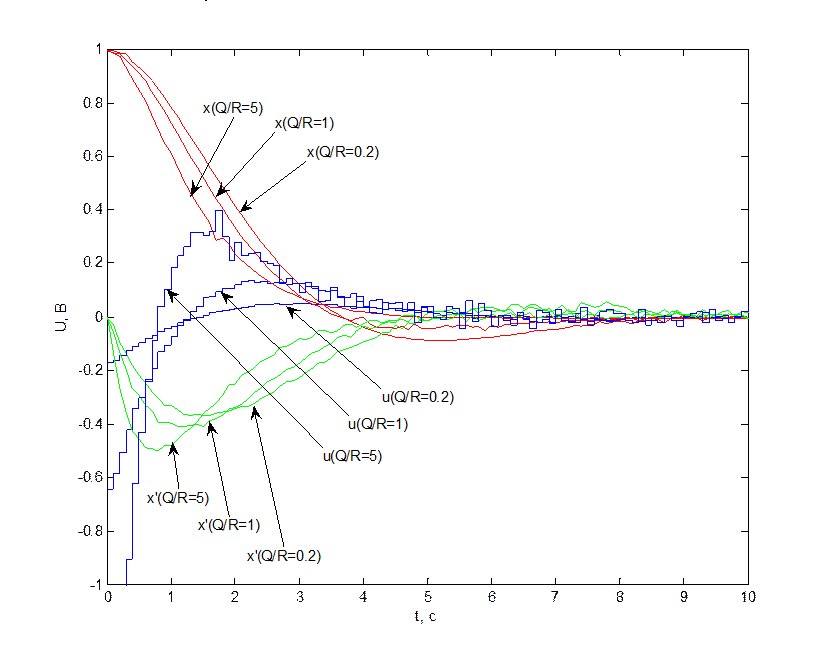
Рис. 4.2.1. Переходные процессы системы при различных отношениях Q/R.

Рис.4.2.2. Управление при различных отношениях Q/R.

4.3. Исследование зависимость оптимальных коэффициентов ОС от отношения параметров критерия J R/Q

На рис. 4.3.1 и рис. 4.3.2. представлены переходные процессы () при разном отношении весов критерия J R/Q. Получаем ситуацию, противоположную п.4.2: при увеличении веса управления по отношению к весу координат колебательность увеличивается, вместе с ней и время переходного процесса, при этом управление, напротив, улучшается.

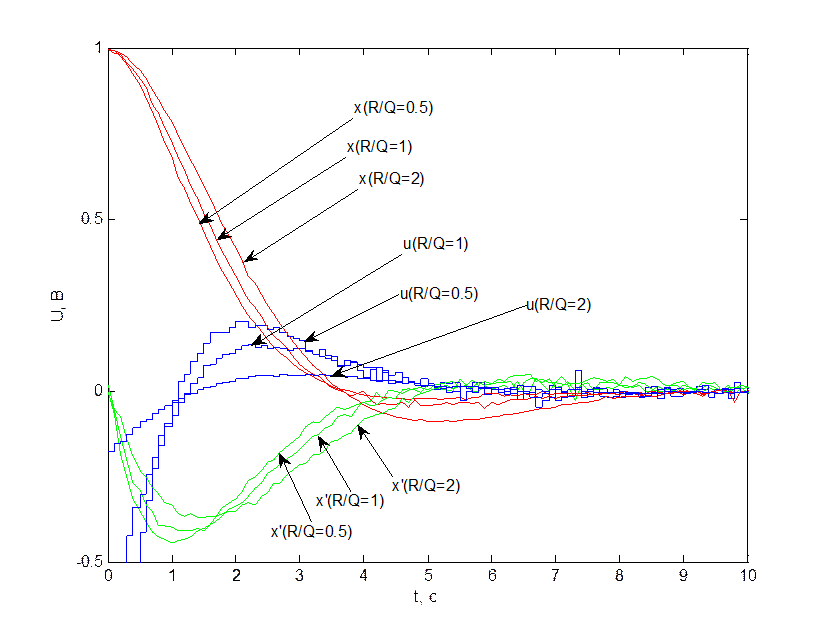
Рис. 4.3.1. Переходные процессы системы при различных отношениях R/Q.

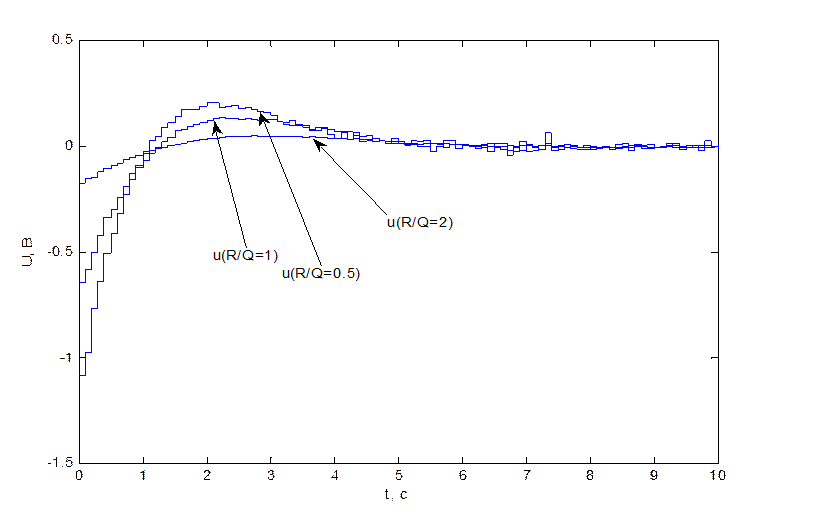
Рис. 4.3.2. Управление при различных отношениях R/Q.

5. Выводы

Анализируя полученные результаты, можно сделать выводы о том, что при правильном расчёте оптимальных коэффициентов можно получить оптимальные характеристики переходного процесса системы. Оптимальными они называются потому, что для улучшения какой-либо составляющей критерия (управления или координаты) мы «жертвуем» второй составляющей. При этом имеет смысл именно отношение весовых коэффициентов критерия. Выводы по каждому разделу исследования приведены в соответствующих пунктах.