«Исследование марковских сетей массового обслуживания (СеМО)»
|
Выполнил ст. гр. ПВТ-111 Гончаров А. В. |
Проверил: Боровских Юрий Васильевич |
1. Открытые СеМО.
Сеть грузовых перевозок состоит из 3-х узлов: морской порт – M|M|3 железнодорожный вокзал – M|M\1, аэропорт – M|M\1. В сеть поступают извне требования с интенсивностями g = (g1, g2, g3). Интенсивность обслуживания в узлах СеМО m = (m1, m2, m3). Матрица маршрутизации имеет вид:
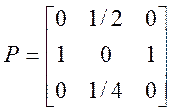
Для стационарного режима работы СеМО определить:
1) Вероятность того, что во всех трех узлах имеется очередь;
2) Вероятность того, что все три узла свободны от грузов;
3) Среднюю длину очереди в морском порту;
4) Распределение времени ожидания в аэропорту;
5) Среднее время ожидания на железнодорожном вокзале;
6) Среднее время пребывания в морском порту;
7) Среднее число грузов в СеМО.
|
№ |
g1 |
g2 |
g3 |
m1 |
m2 |
m3 |
m1 |
m2 |
m3 |
|
+7 |
4 |
1 |
2 |
5 |
20 |
15 |
3 |
1 |
1 |
2. Замкнутые СеМО
Замкнутая система состоит из 4-х узлов [M|M|1]4 и моделирует работу ЭВМ:
1 – процессор;
2 – терминал;
3 – блок памяти;
4 – принтер.
В системе находятся две программы: системная и пользовательская. Причем, если пользовательская программа покидает систему, на е место загружается другая.
Матрица маршрутизации имеет вид:
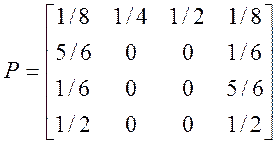
Для стационарного режима работы сети определить:
1) Все возможные состояния системы;
2) Решение уравнений баланса;
3) Нормирующий множитель G(K,N);
4) Вероятности состояний сети pk=(k1, k2, k3, k4);
5) Вероятности состояний каждого узла pi(I), I=0, 1,…,K; i=1,2,…N;
6) Вероятности Pi(Q>=I), I=0, 1,…, K;
7) Среднее число требований в i-ом узле.
1. Расчет открытой СеМО.
1.1) Вероятность того, что вокзал свободен от грузов:
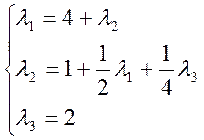
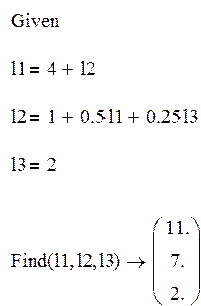 |
ri=li/mi
r1=11/5=2.2; r1/m1=0.733;
r2=7/20=0.35; r2/m2=0.35;
r3=2/15=0.133; r3/m3=0.133;
Стационарный режим для данной СеМО существует.
Вероятность того, что во всех трех узлах есть очередь вычисляется, как произведение вероятностей наличия очередей в каждом узле.
А) Р{В морском порту есть очередь} = 1-p1,0-p1,1-p1,2 .
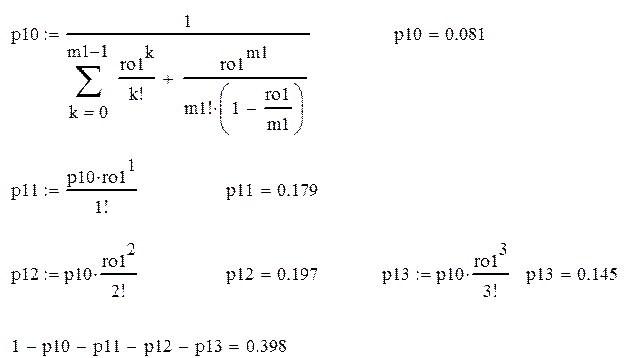 |
Б) P{На Ж/Д вокзале есть очередь}=1-p2,0-p2,1.
1-p2,0-p2,1
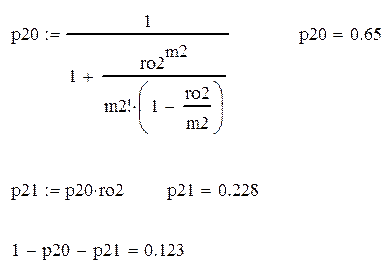 |
В) P{В аэропорту есть очередь}=1-3,0-p3,1.
1-3,0-p3,1
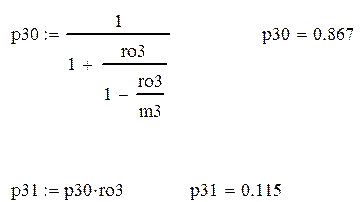 |
Вероятность того, что во всех трех узлах есть очередь: 8.812*10-4.
1.2) Вероятность того, что все узлы свободны от грузов – произведение вероятностей того, что в каждом узле нет клиентов:
P=p1,0*p2,0*p3,0=0.046.
1.3) Средняя длина очереди в морском порту:
qср=p1,3*r1/m1/(1-r1/m1)2=0.497
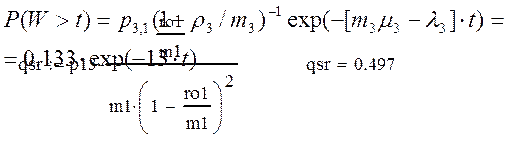
1.4) Распределение времени ожидания в аэропорту:
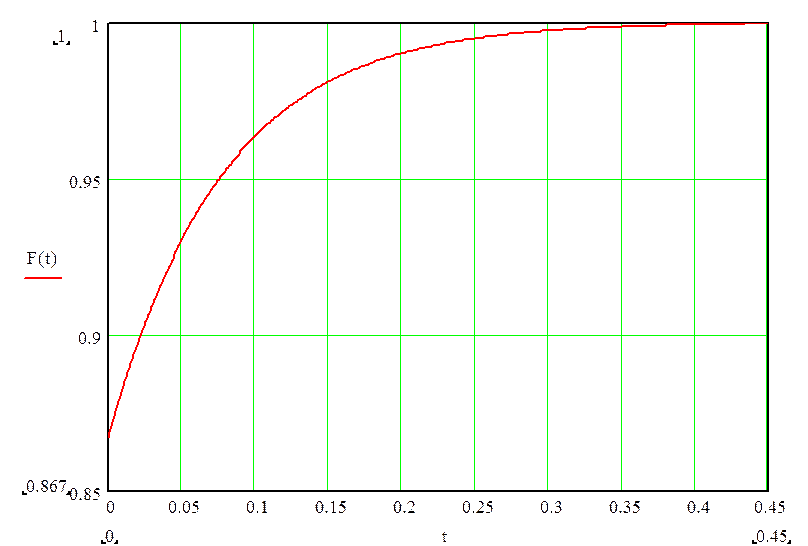 |
1.5) Среднее время ожидания на Ж/Д вокзале:
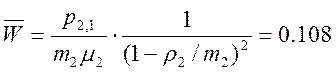
1.6) Среднее время пребывания в морском порту:
W = 1/m1=1/5=0.2
1.7) Среднее число грузов в СеМО: вычисляется к среднее арифметическое среднего числа клиентов в каждом узле.
Q1=0.9/(1-0.9)=9
Q2=0.35/(1-0.35)=0.538
Q3=0.133/(1-0.133)=0.153
2. Рассчет замкнутой СеМО.
2.1) Все возможные состояния системы: число размещений из 5 элементов по 3: число состояний 10.
Перечисление состояний:
(1,1,0,0)
(1,0,0,1)
(0,1,0,1)
(0,0,2,0)
(2,0,0,0)
(1,0,1,0)
(0,1,1,0)
(0,0,1,1)
(0,2,0,0)
(0,0,0,2)
2.2) Уравнение баланса:
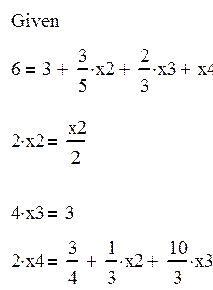 |
Система имеет решение только (1,1,1,1).
2.3) Так как система имеет нулевое решение G(2,4)=10.
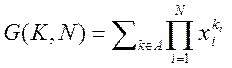
В этой формуле каждое произведение равно единице, а их сумма дает 10.
2.4) Вероятности состояний каждого узла:
pi(0)=3/5, т. к. например, число состояний системы, при котором в первом узле 0 клиентов, равно 6, а все состояний 10.
pi(1)=3/10; pi(2)=1/10.
2.5) Для всех узлов находим:
P(Qi>=1)=2/5, т.к., например, число состояний системы, при которых в первом приборе находятся клиенты, равно 4, а всего состояний 10.
P(Qi>=2)=1/10.
2.6) Среднее число требований в узле.
Для 1-ого узла имеем:
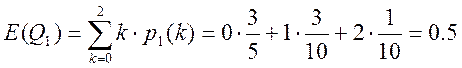
Для остальных узлов вычисления дают те же результаты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.