Активный эксперимент идентификации нелинейной системы. Оптимальный D-план экспериментов для получения модели исследуемой системы с заданной точностью при различных условиях

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра автоматики и вычислительной техники

ОТЧЕТ

по лабораторной работе №2

Дисциплина: идентификация и диагностика систем управления

Тема: активный эксперимент идентификации нелинейной системы

Выполнил студент гр. 5081/11                                                                               

Проверил:                                                                                                                 

Санкт-Петербург

2010

Задание

Сформировать оптимальный D-план экспериментов для получения модели исследуемой системы с заданной точностью при различных условиях.

Модель задана формулой

Программа работы:

1. Исследовать точность модели в зависимости от ее вида, предполагая, что входные величины не имеют погрешности:

linear – линейная,

interaction – линейная + попарные произведения,

purequadratic – квадратичная,

quadratic – квадратичная + попарные произведения.

1.1. Определить диапазон изменения переменных;

1.2. Сформировать D-план (функция cordexch);

1.3. Определить коэффициенты аппроксимирующего полинома (функция rstool);

1.4. Cформировать тестовую случайную последовательность и проверить точность полученной модели по относительной погрешности, нормированной по значению идеальной модели.

2. Исследовать влияние количества экспериментов на получаемую относительную погрешность, построить зависимости значений относительной погрешности для каждой модели от количества экспериментов.

3. Провести моделирование на стохастической системе. Подразумевается, что обучение происходит при снятии значений входных данных с заданной инструментальной погрешностью.

4. Сформулировать выводы о проделанной работе, оформить отчет.

 Выполнение работы

1.1.  Диапазон изменения координат

;        ;      ;      ;     

1.2.  Построение D-плана

Для построения D-плана используется функция MATLAB CORDEXCH (coordinate exchange algorithm).

Входные параметрами данной функции являются:

·  NFACTORS – количество координат (факторов) исследуемой системы;

·  NRUNS – количество экспериментов;

·  MODEL – предполагаемый тип модели.

Результатом работы этой функции является матрица значений факторов  D-оптимального плана.

Рассматриваются следующие типы моделей:

1) linear – содержит константу и линейные слагаемые

2) interaction - содержит константу и линейные слагаемые, а также слагаемые перемноженных координат

3) quadratic - interaction + квадратичные слагаемые

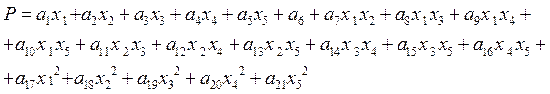
4) purequadratic - содержит константу, линейные и квадратичные слагаемые

Число этапов моделирования для различных типов модели выбираются исходя из числа коэффициентов в аппроксимирующем полиноме:

- linear – 6;

- interaction – 16;

- quadratic – 21;

- purequadratic – 11.

По построенной матрице значений факторов D-оптимального плана с помощью утилиты RSTOOL аппроксимируем  выход системы y по заданным в экспериментах входам x, и получаем коэффициенты аппроксимирующего полинома.

Для каждого типа модели размерность получаемого вектора коэффициентов разная и, в соответствии с этим, тестируем полученную модель на последовательности значений координат. После этого оцениваем адекватность полученной модели.

В соответствии с заданием оценка точности аппроксимации вычисляется по следующей формуле.

где X—случайно сформированный тестовый вектор

Стохастическая система моделируется путем добавления к рассчитанным значениям случайной составляющей с равномерным распределение в диапазоне [0;  0.03*(X_n-X₀)] в соответствии с заданным значением инструментальной погрешности 3%.

1_2.m

Результат: