Neks = 1; % 1 10 % количество экспериментов
Ntest = 100; % 100 1000 10000
delta_linear = 0;
delta_interaction = 0;
delta_purequadratic = 0;
delta_quadratic = 0;
eps_linear = 0;
eps_interaction = 0;
eps_purequadratic = 0;
eps_quadratic = 0;
X1=[1 2];
X2=[2 3];
X3=[3 4];
X4=[4 5];
X5=[5 6];
for k = 1: Neks
for i = 1: Ntest
x1=X1(1)+(X1(2)-X1(1))*rand(1,1);
x2=X2(1)+(X2(2)-X2(1))*rand(1,1);
x3=X3(1)+(X3(2)-X3(1))*rand(1,1);
x4=X4(1)+(X4(2)-X4(1))*rand(1,1);
x5=X5(1)+(X5(2)-X5(1))*rand(1,1);
beta = beta_linear;
y_linear = beta(1) + beta(2)*x1 + beta(3)*x2 + beta(4)*x3+beta(5)*x4+beta(6)*x5;
beta = beta_interaction;
y_interaction = beta(1) + beta(2)*x1 + beta(3)*x2 + beta(4)*x3+beta(5)*x4+beta(6)*x5...
+beta(7)*x1*x2+beta(8)*x1*x3+beta(9)*x1*x4+beta(10)*x1*x5+beta(11)*x2*x3...
+beta(12)*x2*x4 +beta(13)*x2*x5+beta(14)*x3*x4+beta(15)*x3*x5+beta(16)*x4*x5;
beta = beta_quadratic;
y_quadratic = beta(1) + beta(2)*x1 + beta(3)*x2 + beta(4)*x3+beta(5)*x4+beta(6)*x5...
+beta(7)*x1*x2+beta(8)*x1*x3+beta(9)*x1*x4+beta(10)*x1*x5+beta(11)*x2*x3...
+beta(12)*x2*x4 +beta(13)*x2*x5+beta(14)*x3*x4+beta(15)*x3*x5+beta(16)*x4*x5...
+beta(17)*x1*x1+beta(18)*x2*x2+beta(19)*x3*x3+beta(20)*x4*x4+beta(21)*x5*x5;
beta = beta_purequadratic;
y_purequadratic = beta(1) + beta(2)*x1 + beta(3)*x2 + beta(4)*x3+beta(5)*x4+beta(6)*x5...
+beta(7)*x1*x1+beta(8)*x2*x2+beta(9)*x3*x3+beta(10)*x4*x4+beta(11)*x5*x5;
yt = ((x2.^3).*x3)+x1+(x5.^x4);
delta_linear(i)= abs((y_linear-yt)/yt);
delta_interaction(i)= abs((y_interaction-yt)/yt);
delta_quadratic(i)= abs((y_quadratic-yt)/yt);
delta_purequadratic(i)= abs((y_purequadratic-yt)/yt);
end
eps_linear(k) = mean(delta_linear);
eps_interaction(k) = mean(delta_interaction);
eps_quadratic(k) = mean(delta_quadratic);
eps_purequadratic(k) = mean(delta_purequadratic);
end
eps_mean_linear = mean(eps_linear)
eps_mean_interaction = mean(eps_interaction)
eps_mean_quadratic = mean(eps_quadratic)
eps_mean_purequadratic = mean(eps_purequadratic)
Результаты экспериментов:
Таблица 1.4. Результаты проверки точности полученной модели.
|
Погрешность |
||||||
|
Выборка |
100 |
1000 |
10000 |
|||
|
Модель |
Neks=1 |
Neks=10 |
Neks=1 |
Neks=10 |
Neks=1 |
Neks=10 |
|
linear |
0.3802 |
0.3986 |
0.3866 |
0.3884 |
0.3884 |
0.3874 |
|
interaction |
0.2955 |
0.2969 |
0.2993 |
0.2948 |
0.2968 |
0.2955 |
|
quadratic |
0.1096 |
0.1080 |
0.1087 |
0.1060 |
0.1073 |
0.1065 |
|
purequadratic |
0.2506 |
0.2696 |
0.2680 |
0.2650 |
0.2623 |
0.2623 |
2. Исследование влияния количества экспериментов на получаемую относительную погрешность.
2.m
x = [ 100; 1000; 10000];
y1 = [0.3802 ;0.3866; 0.3884];
y2 = [0.3986;0.3884;0.3874];
y3 = [0.2955;0.2993;0.2968 ];
y4 = [0.2969;0.2948;0.2955];
y5 = [0.1096;0.1087;0.1073 ];
y6 = [ 0.1080;0.1060;0.1065 ];
y7 = [0.3506;0.2680;0.2623];
y8 = [ 0.2696;0.2650;0.2623];
plot(x,y1,'b');
hold on
plot(x,y2,'b--');
hold on
plot(x,y3,'g');
hold on
plot(x,y4,'g--');
hold on
plot(x,y5,'r');
hold on
plot(x,y6,'r--');
hold on
plot(x,y7,'k');
hold on
plot(x,y8,'k--');
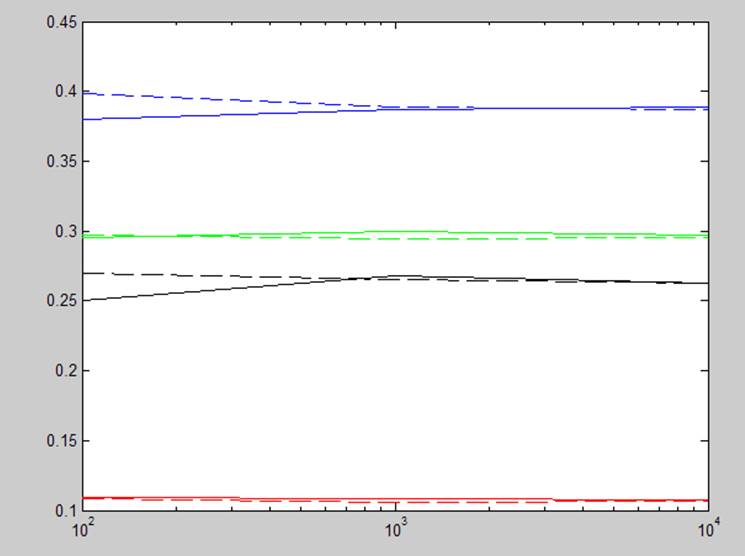
Рис. 2. Зависимость погрешности от размера выборки при различных типах моделей и количестве экспериментов. синяя – linear; черная – purequadratic; зеленая – interaction; красная – quadratic; пунктир – Neks=10
3. Моделирование на стохастической системе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.