3.m
NFACTORS = 5;
x1=[1 2];
x2=[2 3];
x3=[3 4];
x4=[4 5];
x5=[5 6];
X=[(x1(1)+x1(2))/2 (x1(2)-x1(1))/2;
(x2(2)+x2(1))/2 (x2(2)-x2(1))/2;
(x3(2)+x3(1))/2 (x3(2)-x3(1))/2;
(x4(2)+x4(1))/2 (x4(2)-x4(1))/2;
(x5(2)+x5(1))/2 (x5(2)-x5(1))/2];
NRUNS = 6;
S = S_linear;
for i=1:NRUNS
for j=1:NFACTORS
XRES(i,j)=X(j,1)+X(j,2)*S(i,j);
XRES(i,j)=XRES(i,j)*(1 + 0.04*rand(1,1)*sign(randn(1)));
end
end
Y= (XRES(:,2).^3).*XRES(:,3)+XRES(:,1)+(XRES(:,5).^XRES(:,4));
rstool(XRES,Y,'linear')
echo off, pause
beta_linear = beta
NRUNS = 16;
S = S_interaction;
for i=1:NRUNS
for j=1:NFACTORS
XRES(i,j)=X(j,1)+X(j,2)*S(i,j);
XRES(i,j)=XRES(i,j)*(1 + 0.04*rand(1,1)*sign(randn(1)));
end
end
Y= (XRES(:,2).^3).*XRES(:,3)+XRES(:,1)+(XRES(:,5).^XRES(:,4));
rstool(XRES,Y,'interaction')
echo off, pause
beta_interaction = beta1
NRUNS = 21;
S = S_quadratic;
for i=1:NRUNS
for j=1:NFACTORS
XRES(i,j)=X(j,1)+X(j,2)*S(i,j);
XRES(i,j)=XRES(i,j)*(1 + 0.04*rand(1,1)*sign(randn(1)));
end
end
Y= (XRES(:,2).^3).*XRES(:,3)+XRES(:,1)+(XRES(:,5).^XRES(:,4));
rstool(XRES,Y,'quadratic')
echo off, pause
beta_quadratic = beta2
NRUNS = 11;
S = S_purequadratic;
for i=1:NRUNS
for j=1:NFACTORS
XRES(i,j)=X(j,1)+X(j,2)*S(i,j);
XRES(i,j)=XRES(i,j)*(1 + 0.04*rand(1,1)*sign(randn(1)));
end
end
Y= (XRES(:,2).^3).*XRES(:,3)+XRES(:,1)+(XRES(:,5).^XRES(:,4));
rstool(XRES,Y,'purequadratic')
echo off, pause
beta_purequadratic = beta3
Результаты:
beta_linear =
1.0e+004 *
-2.3656
-0.0609
-0.0846
-0.0477
0.4432
0.2114
Variables have been created in the current workspace.
beta_interaction =
1.0e+004 *
7.6962
0.9046
0.1256
-0.8945
-1.6910
-1.7265
-0.0913
0.0018
-0.0723
-0.0650
0.0343
-0.0326
0.0108
0.0630
0.1015
0.3849
Variables have been created in the current workspace.
beta_quadratic =
1.0e+005 *
2.1533
0.0572
0.0217
-0.0676
-0.6597
-0.2844
0.0032
0.0003
0.0015
-0.0003
0.0014
0.0006
-0.0026
-0.0063
0.0069
0.0410
-0.0239
-0.0035
0.0080
0.0550
0.0101
Variables have been created in the current workspace.
beta_purequadratic =
1.0e+004 *
2.6470
0.1172
-0.0777
-1.5590
0.1165
-0.4635
-0.0584
-0.0025
0.2223
0.0341
0.0605
Относительная погрешность:
Результаты экспериментов:
Таблица 3. Результаты проверки точности полученной модели.
|
Погрешность |
||||||
|
Выборка |
100 |
1000 |
10000 |
|||
|
Модель |
Neks=1 |
Neks=10 |
Neks=1 |
Neks=10 |
Neks=1 |
Neks=10 |
|
linear |
0.3757 |
0.3749 |
0.3544 |
0.3640 |
0.3669 |
0.3627 |
|
interaction |
0.3318 |
0.3392 |
0.3346 |
0.3333 |
0.3347 |
0.3339 |
|
quadratic |
0.1550 |
0.1674 |
0.1622 |
0.1598 |
0.1578 |
0.1610 |
|
purequadratic |
0.2141 |
0.2258 |
0.2181 |
0.2289 |
0.2282 |
0.2291 |
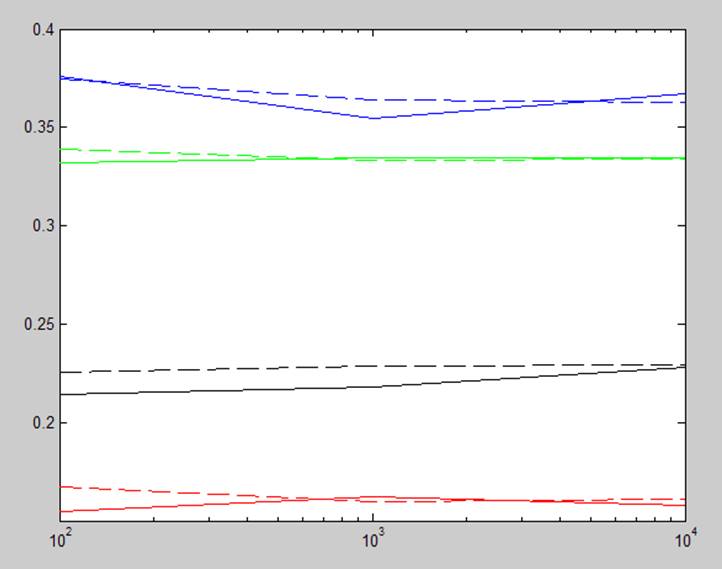
Рис. 3. Зависимость погрешности от размера выборки при различных типах моделей и количестве экспериментов. синяя – linear; черная – purequadratic; зеленая – interaction; красная – quadratic; пунктир – Neks=10
4. Выводы
В данной лабораторной работе был получен D-план. Этот план эксперимента позволяет за минимальное число опытов получить максимальное количество информации об объекте.
Для заданной системы был построен аппроксимирующий полином соответствующего вида. На заданных интервалах изменения переменных наименьшей погрешностью обладает наиболее сложная модель вида квадратичной функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.