Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра автоматики и вычислительной техники
по лабораторной работе №5
Дисциплина: идентификация и диагностика систем управления
Тема: Моделирование системы диагностирования, построенной с использованием метода избыточных переменных
Выполнил студент гр. 5081/1
Проверил:
Санкт-Петербург
2009
1. Задание
Исследовать систему диагностирования, построенную с использованием метода избыточных переменных. Объект диагностирования (ОД) задан уравнением в пространства состояний:
![]() ,
,
![]() ,
,
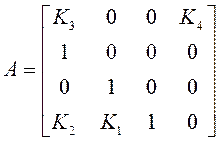 ,
,
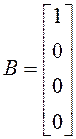 ,
, 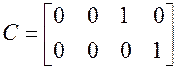 ,
,
На вход ОД поступает ступенчатое воздействие.
Программа работы:
1. Синтезировать устройство диагностирования, используя метод избыточных переменных.
2. Провести моделирование системы в режиме нормального функционирования, построить графики выходов объекта, переменных состояния объекта, выхода устройства диагностирования и построенного инварианта.
3. Определить следующие типы дефектов:
1) Увеличение K1 на 50% (базовое значение);
2) Уменьшение K1 на 50% (базовое значение);
3) Увеличение K2 на 50% (базовое значение);
4) Уменьшение K2 на 50% (базовое значение);
5) Увеличение K3 на 50% (базовое значение);
6) Уменьшение K3 на 50% (базовое значение);
7) Увеличение K4 на 50% (базовое значение);
8) Уменьшение K4 на 50% (базовое значение).
Провести моделирование системы в режиме функционирования с дефектом, построить графики выходов объекта, переменных состояния объекта, выхода устройства диагностирования и построенного инварианта.
4. Сформулировать выводы о проделанной работе, оформить отчет.
|
Вариант |
|
|
|
|
Типы дефектов |
|
1 |
2 |
2 |
–3 |
–5 |
1,2,3,4 |
Теория
Метод избыточных переменных
Предполагается, что объект диагностирования - линейный стационарный и задан уравнением в пространстве состояний и наблюдений:
![]()
Устройство диагностирования вырабатывает сигнал z, который при любом входном сигнале u(t) и в любой момент времени удовлетворяет условию:
![]()
где MT – строка постоянных коэффициентов.
Если в результате непрерывного функционирования объекта диагностирования произошло искажение его выходных сигналов по причине возникновения дефекта, это должно привести к нарушению контрольного уравнения и появлению сигнала рассогласования Δ(t)≠0.
Предполагая, что структура устройства диагностирования имеет вид, представленный на рисунке 1.1, получены необходимые и достаточные условия существования УД порядка k:
1. 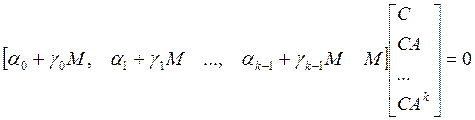
2. ![]()
3. ![]()
…
k. ![]()
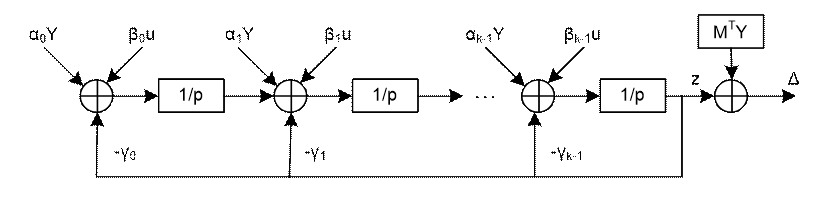 Рис. 1.1. Структура
устройства диагностирования
Рис. 1.1. Структура
устройства диагностирования
Верно следующее утверждение:
минимальный порядок УД заданного вида при любом входном сигнале u(t) и любом векторе M равен индексу наблюдаемости проверяемой системы v0. Индексом наблюдаемости здесь называется
наименьшее целое положительное число, для которого ![]() . Можно показать,
что индекс наблюдаемости системы произвольного порядка удовлетворяет
неравенству:
. Можно показать,
что индекс наблюдаемости системы произвольного порядка удовлетворяет
неравенству:
![]()
где n – размерность вектора x, s – размерность вектора y.
Методика синтеза выглядит следующим образом:
1. Находим минимальный порядок k для УД.
2. Для выбранного вектора M находим значения компонент вектора αl.
3. Определяем значения векторов ![]() .
.
4. Выходной сигнал z моделируется в виде:
![]()
скалярные коэффициенты ![]() приняты здесь
равными нулю.
приняты здесь
равными нулю.
2. Выполнение работы
1) определим минимальный порядок УД. В данном случае n=4, s=2:
![]() =>
=> ![]()
2) Пусть M=[1; 1]
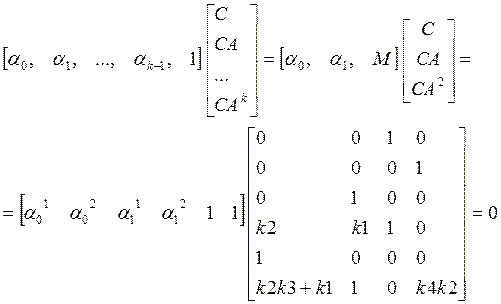
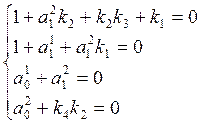 =>
=>
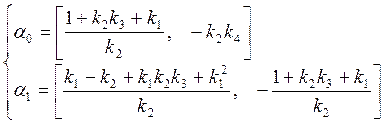
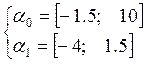
3) ![]()
![]()
4) ![]()
![]()
![]()
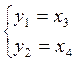
![]()
![]()
![]()
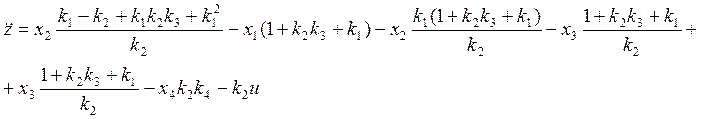
![]()
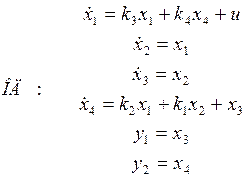
![]()
Перейдем к дискретной форме представления сигнала.
![]()
![]()
![]()
![]()
Для испытания совместного функционирования объекта диагностирования (ОД) и устройства диагностирования (УД), исследуем переходную характеристику системы без дефекта и с различными дефектами.
lab5.m
clc;
%---------------------------------k1 = 2;
k2 = 2;
k1d = 2; % дефект k1 % 1 2 3
k2d = 2; % дефект k2 % 1 2 3
k3 = -3;
k4 = -5;
t = 0.001;
Tf = 20;
a00 = (1+k2*k3+k1)/k2;
a01 = -k2*k4;
a10 = (k1-k2+k1*k2*k3+k1*k1)/k2;
a11 = -(1+k2*k3+k1)/k2;
M = [1 1];
B = [1;0;0;0];
C = [0 0 1 0;0 0 0 1];
D = [0;0];
A = [k3, 0, 0, k4; 1, 0, 0, 0; 0, 1, 0, 0; k2, k1, 1, 0];
Ad = [k3, 0, 0, k4; 1, 0, 0, 0; 0, 1, 0, 0; k2d, k1d, 1, 0];
b1 = -M*(C*B);
b0 = -(M*(C*A)+[a10 a11]*C)*B;
%-----------------------------------------------T = [0:t:Tf];
sys = ss(Ad,B,C,D);
[Y,T,X] = step(sys,T);
figure
step(sys,T);
grid on
[m,n] = size(Y);
U = ones(m,1);
Z = zeros(m,1);
I = zeros(m,1);
Z(1) = t^2*(-X(1,1)*(1+k2*k3+k1)-X(1,2)-X(1,4)*k2*k4-k2*U(1));
Z(2) = 2*Z(1) + t^2*(-X(2,1)*(1+k2*k3+k1)-X(2,2)-X(2,4)*k2*k4-k2*U(2));
for i = 3:m
Z(i) = 2*Z(i-1) - Z(i-2) + t^2*(-X(i,1)*(1+k2*k3+k1)-X(i,2)-X(i,4)*k2*k4-k2*U(i));
end
for i = 1:m
I(i) = X(i,3) + X(i,4) + Z(i) + t^2*i;
end
figure
grid on
subplot(2,1,1);
plot(T,I);
grid on
xlabel('t');
ylabel('MY+z');
subplot(2,1,2);
plot(T, Z);
grid on
xlabel('t');
ylabel('z');
Моделирование системы в режиме нормального функционирования (без дефектов).
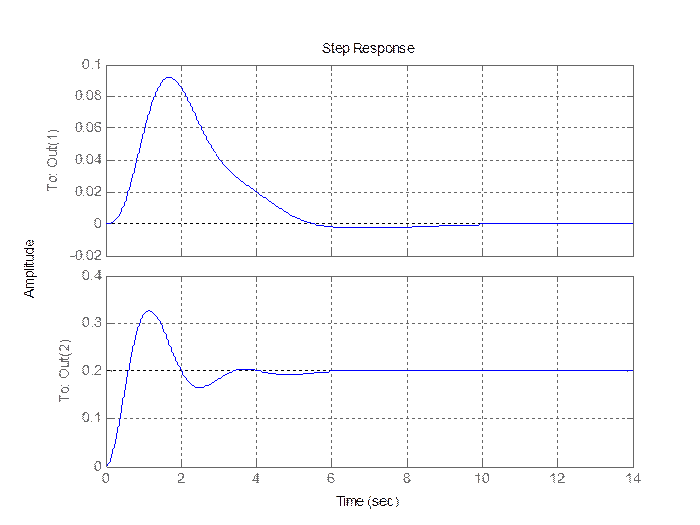
Рис. 2.1. Выход объекта диагностирования.
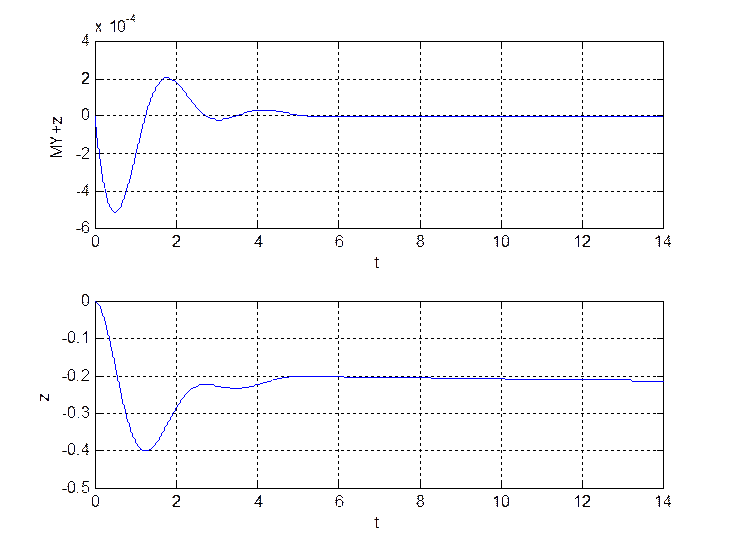
Рис. 2.2. Выход устройства диагностирования.
В режиме нормального функционирования инвариант ![]() . Переходный
процесс объекта диагностирования затухающий:
. Переходный
процесс объекта диагностирования затухающий: ![]() .
.
Моделирование системы в режиме функционирования с дефектом:
Увеличение K1 на 50% (базовое значение): k1d = 3;
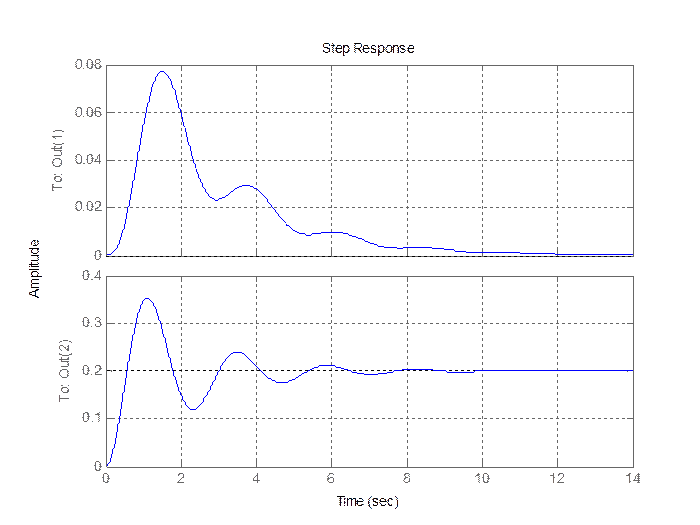
Рис. 2.3. Выход объекта диагностирования.
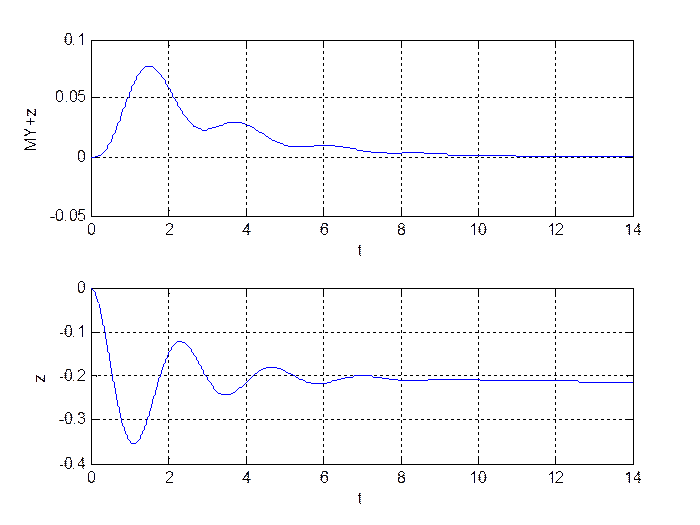
Рис. 2.4. Выход устройства диагностирования.
В режиме функционирования с дефектом (увеличение К1 на 50%)
инвариант ![]() меняет своё значение, что и является признаком наличия дефекта, и
становится равным нулю только после окончания переходного процесса в системе.
меняет своё значение, что и является признаком наличия дефекта, и
становится равным нулю только после окончания переходного процесса в системе.
Уменьшение K1 на 50% (базовое значение): k1d = 1;
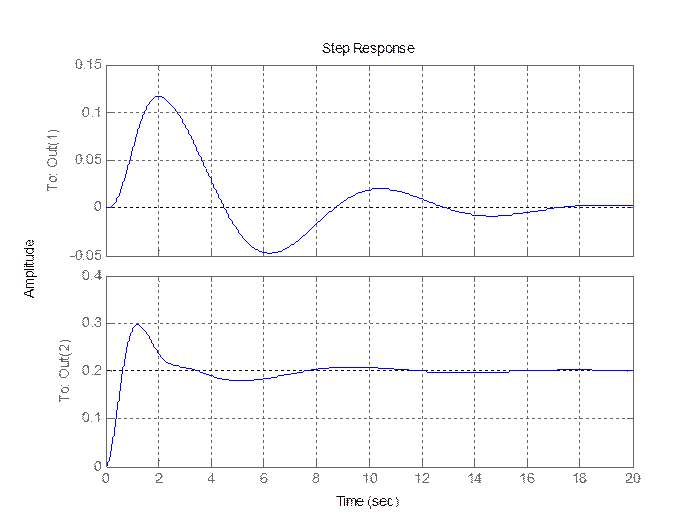
Рис. 2.5. Выход объекта диагностирования.
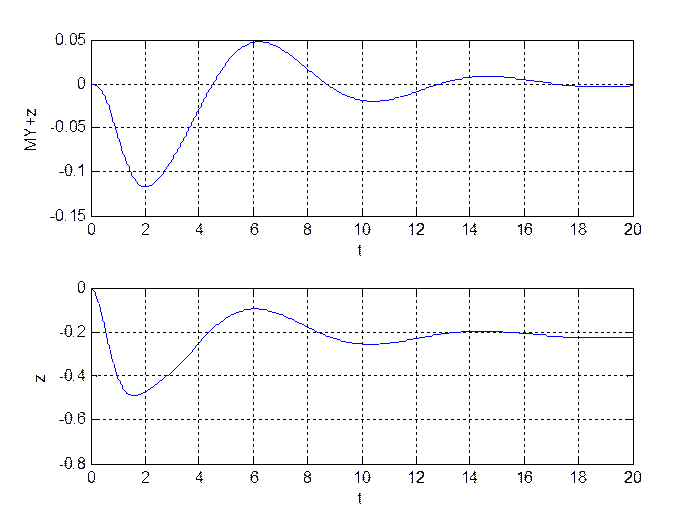
Рис. 2.6. Выход устройства диагностирования.
Увеличение K2 на 50% (базовое значение): k2d = 3
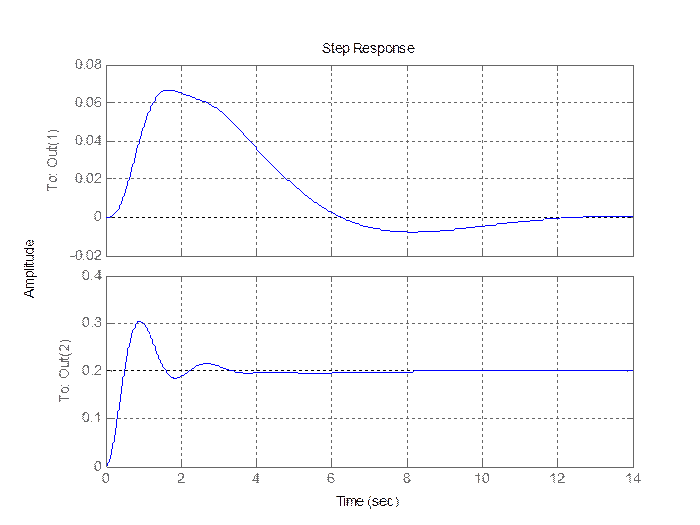
Рис. 2.7. Выход объекта диагностирования.
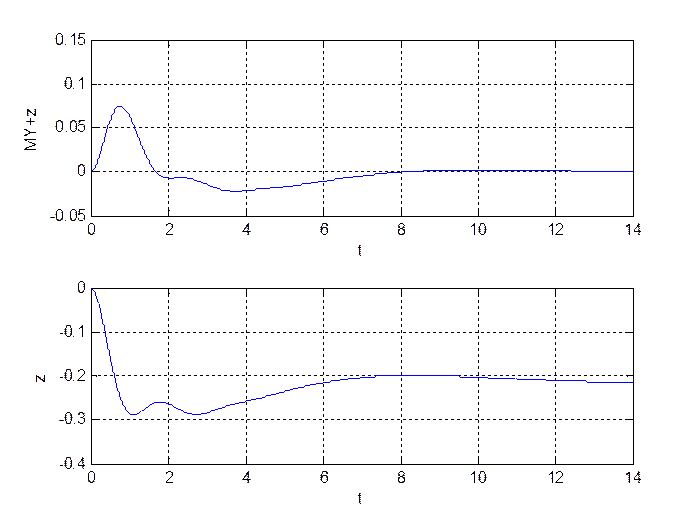
Рис. 2.8. Выход устройства диагностирования.
Уменьшение K2 на 50% (базовое значение): k2d = 1
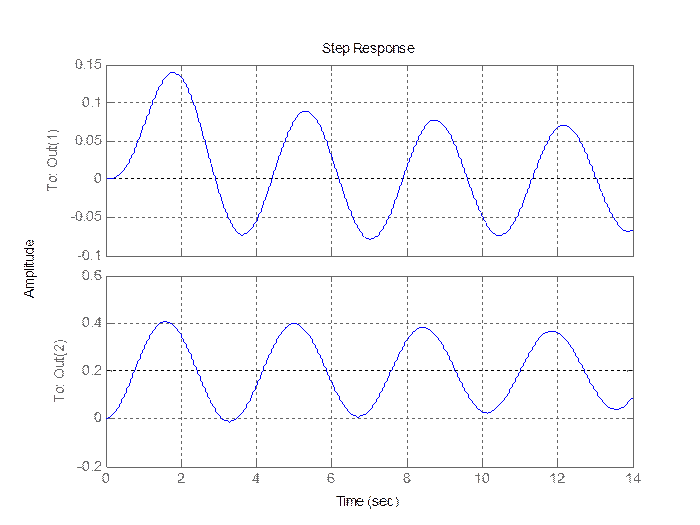
Рис. 2.9. Выход объекта диагностирования.
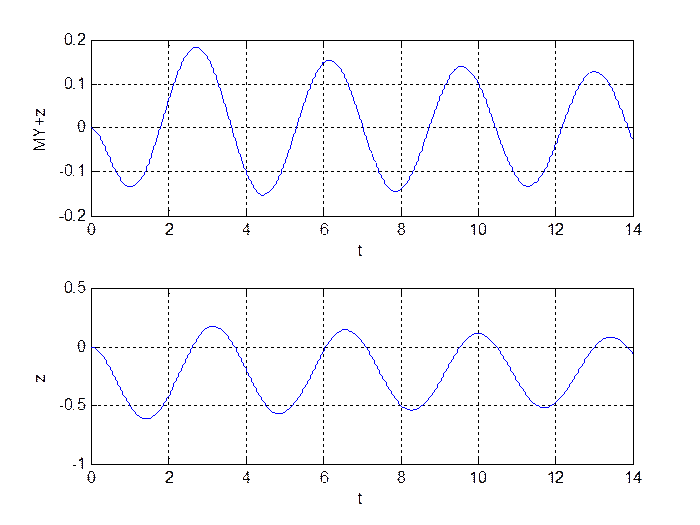
Рис. 2.10. Выход устройства диагностирования.
3. Выводы
В рамках данной работы производилось построение устройства диагностирования на основе метода избыточных переменных.
Было произведено моделирование работы системы в различных условиях – в нормальных условиях и при изменении отдельных параметров объекта диагностирования. При этом состояние системы оценивалось с помощью единичного ступенчатого воздействия, а результат диагностирования наблюдался по выходу синтезированного устройства диагностирования.
При отсутствии дефекта построенный инвариант равен нулю, небольшие отклонения могут быть связаны с величиной шага квантования, уменьшением t можно добиться уменьшения отклонения. При появлении дефекта в системе выход сигнала устройства
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.