Линейное дифференциальное уравнение второго порядка. Рекуррентный метод наименьших квадратов

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ

КАФЕДРА АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Расчетное задание 3

Дисциплина: Адаптивные системы управления

Работу выполнил студент     5081/2            

группа                           ФИО

Преподаватель                          

подпись                            ФИО

Санкт-Петербург

2009г.

Задание

Рассматривается объект, математическая модель которого - линейное дифференциальное уравнение второго порядка:

Требуется:

Исследовать системы идентификации параметров объекта в разомкнутой и замкнутой системе. Использовать два метода:

- рекуррентный метод наименьших квадратов,

- алгоритм Качмажа.

Теоретические положения

1. Рекуррентный метод наименьших квадратов

Метод имеет в своей основе минимизацию функции:

Вычисление оценок параметров объекта производятся рекуррентно, т.е. на основании текущих измерений и значений параметров полученных на предыдущем шаге.

- вектор оценки неизвестных параметров после N-го измерения.

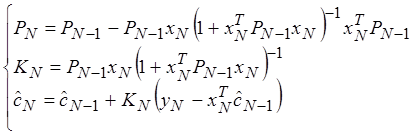
2. Алгоритм Качмажа

Идея метода состоит в решении задачи условной минимизации, когда новая оценка строится на минимальных изменениях старой. Целевая функция:

Рабочая формула алгоритма:

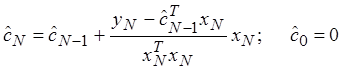
Исходные данные

a₀ = 5 , a₁ =                α = 1, β = 0

Получаем следующее уравнение объекта:

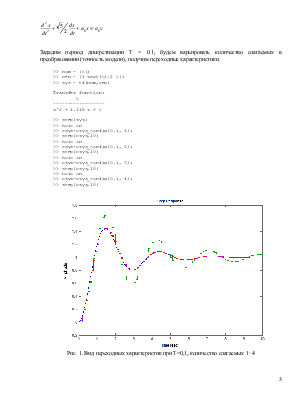
Зададим период дискретизации T = 0.1, будем варьировать количество слагаемых в преобразовании (точность модели), получим переходные характеристики.

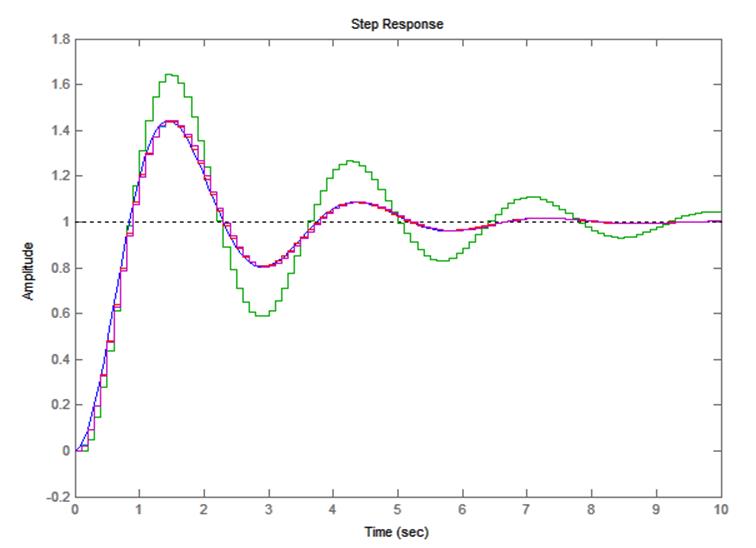
Рис. 1. Вид переходных характеристик при T=0,1, количество слагаемых 1÷4

Для решения обратной задачи перехода от дискретной к непрерывной системе переход от некоторой реализации R(Ф, Г, С) дискретной системы к некоторой реализации R*(A*, B*, H*) непрерывной системы может быть осуществлен с помощью следующих соотношений:

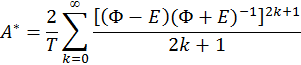
Переход к дискретной форме описания:

Модель системы без сигнальных помех:

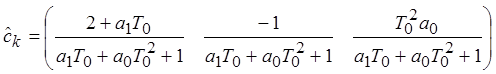
Составим уравнения для обратного преобразования оценочных коэффициентов в параметры системы:

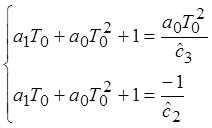
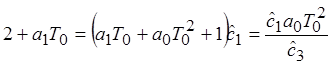
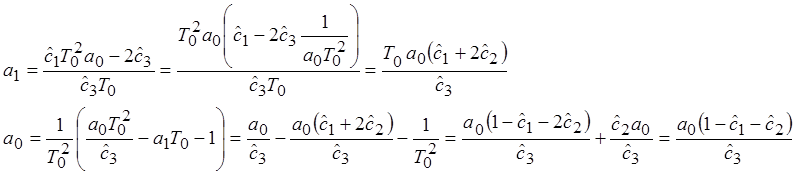
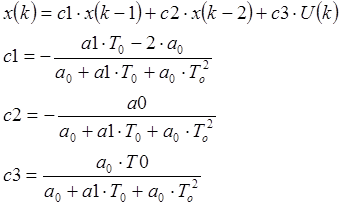
Результаты исследования

1. Рекуррентный метод наименьших квадратов.

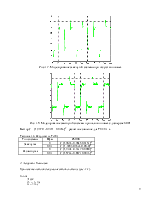
Применение метода для разомкнутой системы

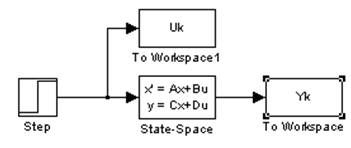
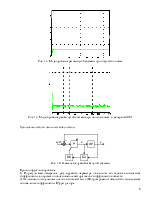
Рис. 1.1. Модель системы в Simulink

r3.1.m

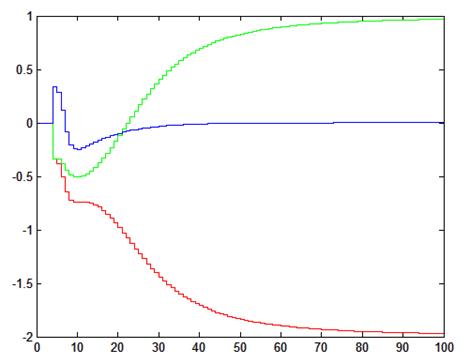
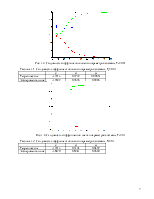
Рис. 1.2. Сходимость коэффициентов оценки параметров системы, Т₀=0,01

Таблица 1.1. Сходимость коэффициентов оценки параметров системы, Т₀=0,01