Санкт-Петербургский государственный политехнический университет
Кафедра компьютерных систем и программных технологий
Расчётное задание
Дисциплина: Адаптивные системы управления
Тема: Построение и исследование процессов в беспоисковой адаптивной системе прямого типа
Выполнил студент группы 5081/1 подпись
Преподаватель С.
подпись
Санкт-Петербург
2011
1. Задание
Задан объект, описываемый линейным дифференциальным уравнением 2-го порядка:
![]()
Синтезировать и исследовать беспоисковую адаптивную систему с эталонной моделью.
2. Исходные данные
![]()
Получим следующее уравнение:
![]()
3. Теоретические сведения
Структура БАС с параллельной эталонной моделью представлена на рис. 3.
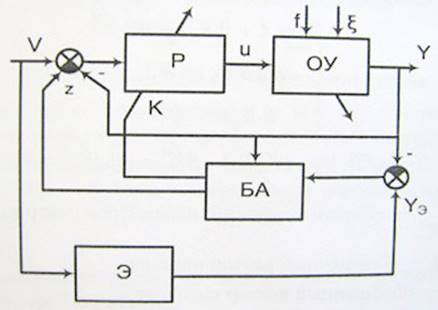
Рис. 3. Структура БАСЭМ
Прямой подход связан с использованием эталона, под который подстраивается движение всей системы или её части. Коррекция осуществляется без дополнительной идентификации на основе минимизации функционала качества от рассогласования эталона и реальной системы.
В работе будет применён метод скоростного градиента. В градиентных методах направление движения в алгоритмах определялось изменением направления самого градиента. В алгоритмах МСГ осуществляется движение в каждый момент времени противоположно градиенту скорости изменения функционала качества.
![]()
Цель: ![]()
Скорость: ![]()
![]()
![]()
![]()
4. Выполнение работы
4.1. Разработка БАСЭМ
На рис. 4.1 представлена схема системы в Simulink.
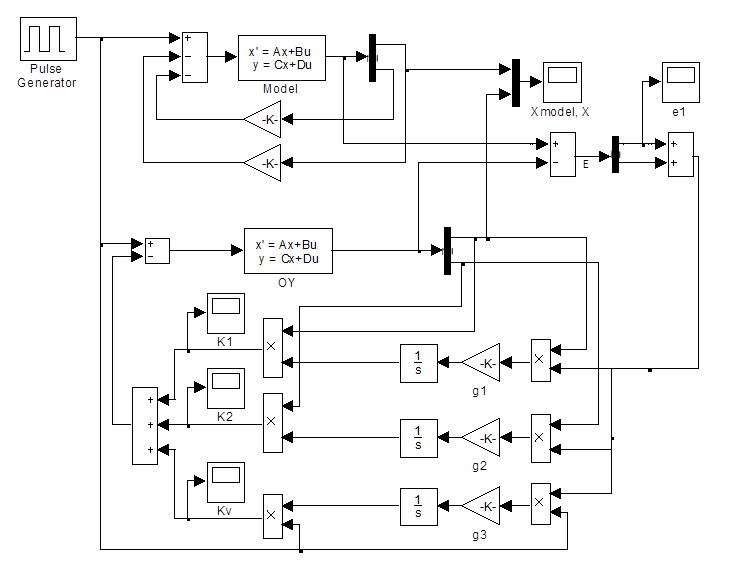
Рис. 4.1. Схема исследуемой системы в Simulink
Параметры объекта и модели полностью совпадают.
k1 = 0,414
k2 = 0,241
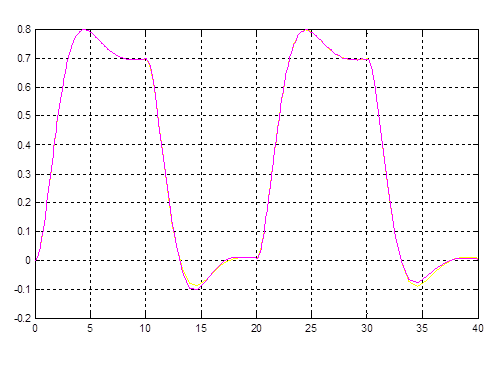
Рис. 4.1. Выходы первичного и эталонного контуров
Графики выходов совпадают.
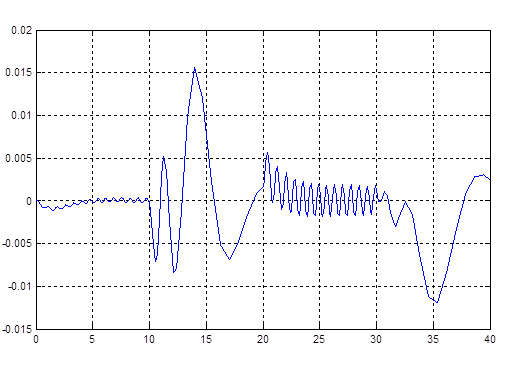
Рис. 4.2. Ошибка по x (рассогласование эталона и реальной системы)
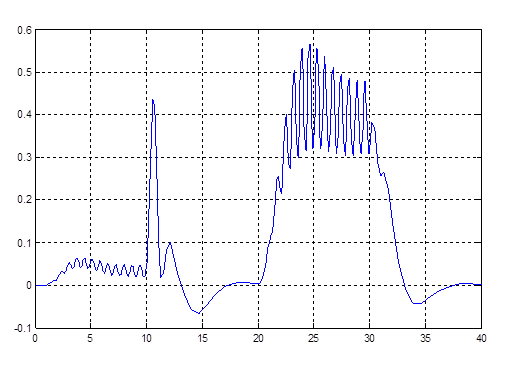
Рис. 4.3. График k1
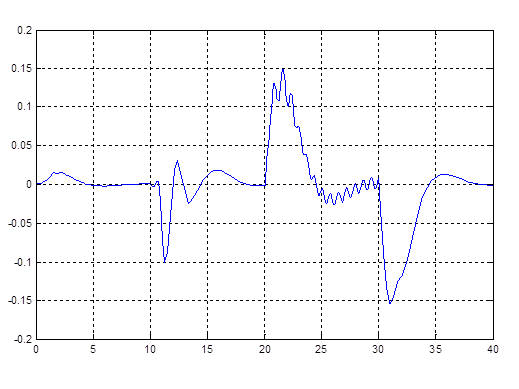
Рис. 4.4. График k2
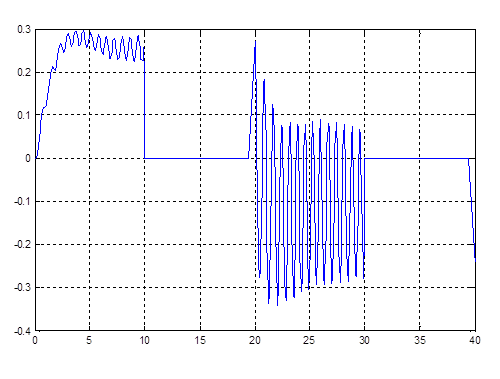
Рис. 4.5. График kv
Увеличим a0 в 10 раз.
a0 = 5
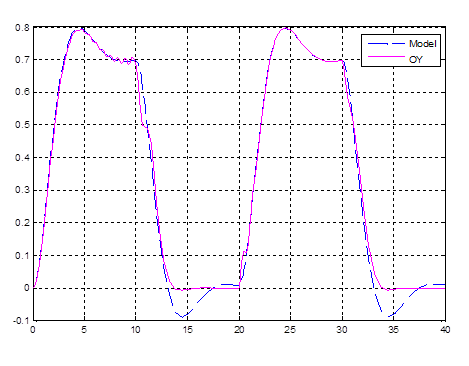
Рис. 4.6. Выходы первичного и эталонного контуров
Графики практически повторяют друг друга.
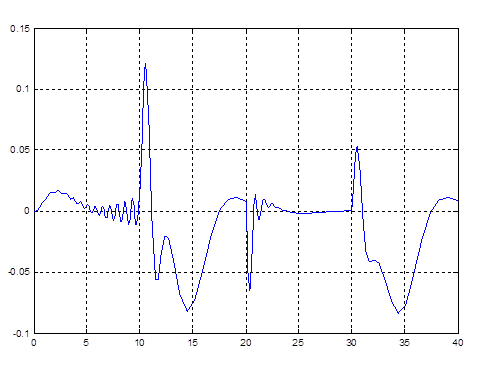
Рис. 4.7. Ошибка по x (рассогласование эталона и реальной системы)
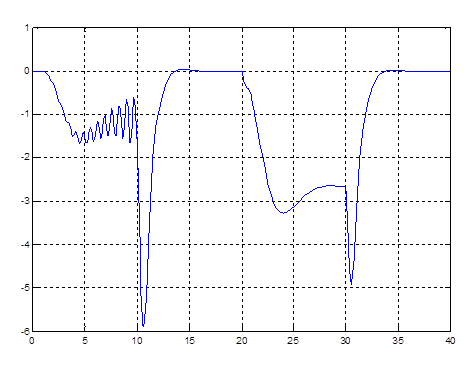
Рис. 4.8. График k1
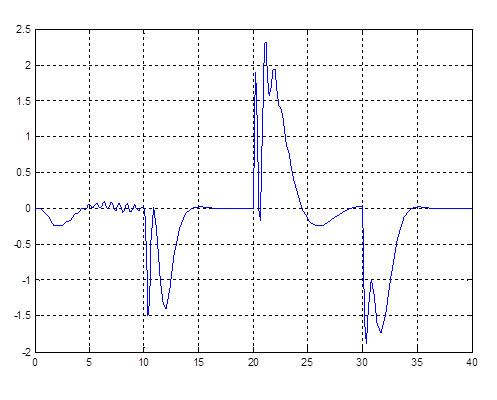
Рис. 4.9. График k2
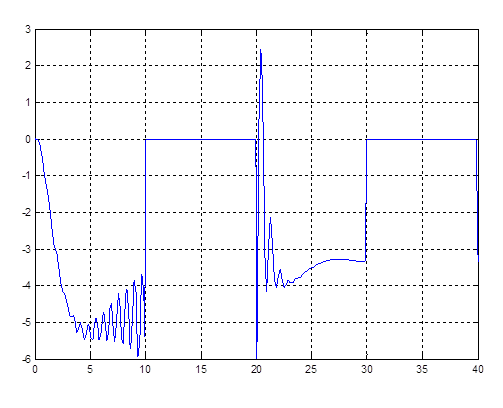
Рис. 4.10. График kv
Уменьшим начальное значение a0 в 10 раз.
a0 = 0,05
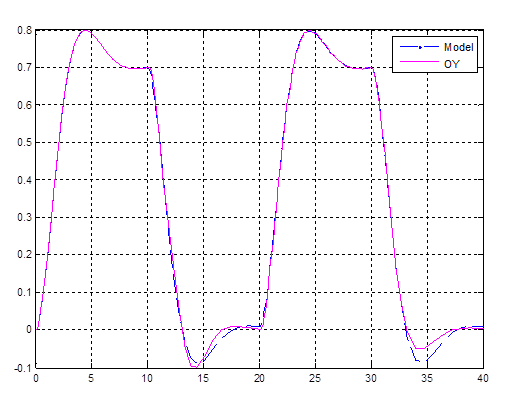
Рис. 4.11. Выходы первичного и эталонного контуров
Графики практически повторяют друг друга.
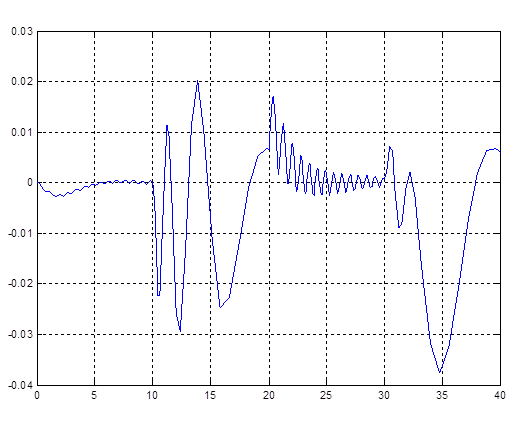
Рис. 4.12. Ошибка по x (рассогласование эталона и реальной системы)
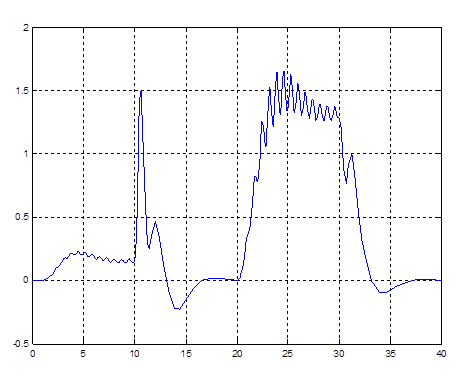
Рис. 4.13. График k1
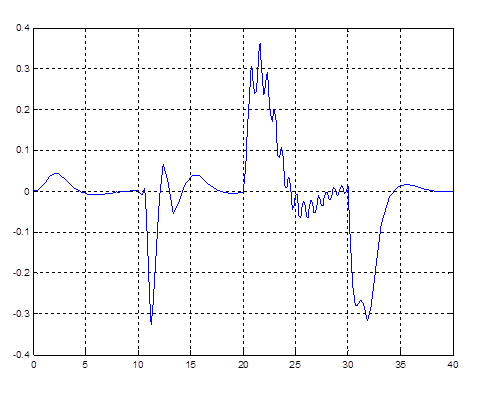
Рис. 4.14. График k2
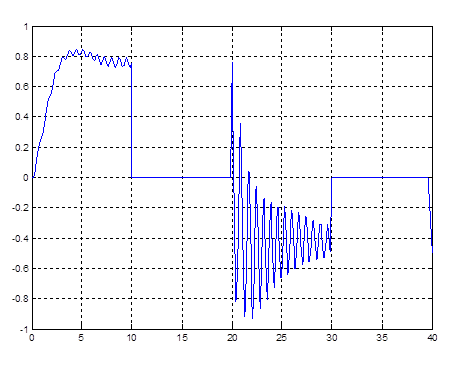
Рис. 4.15. График kv
4.2. Добавление пропорциональной составляющей
Схема в Simulink представлена на рис. 4.16.
Увеличим a0 в 2 раза и посмотрим на рассогласование контуров. С введением новой составляющей ошибка должна заметно уменьшиться.
a0 = 1
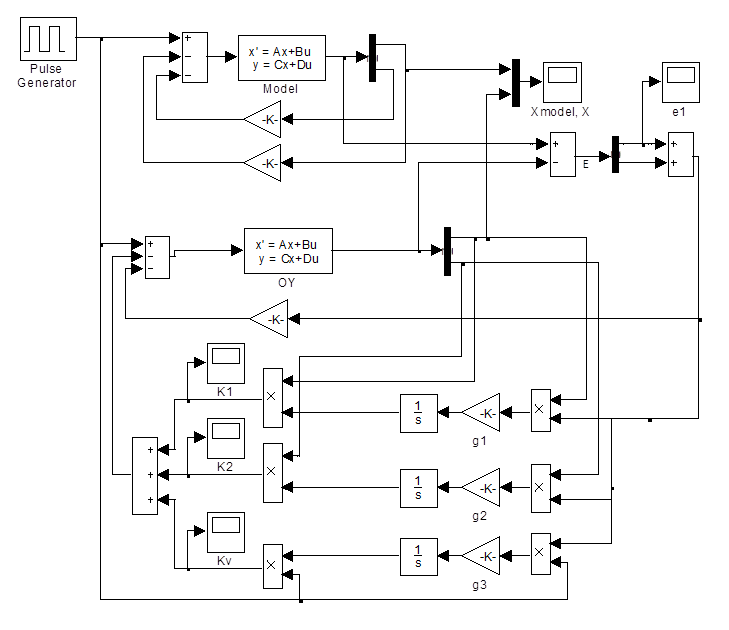
Рис. 4.16. Схема системы в Simulink
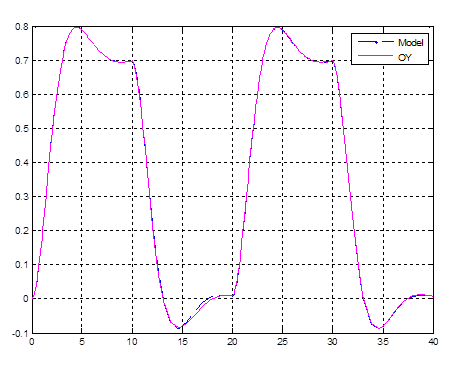
Рис. 4.17. Выходы первичного и эталонного контуров
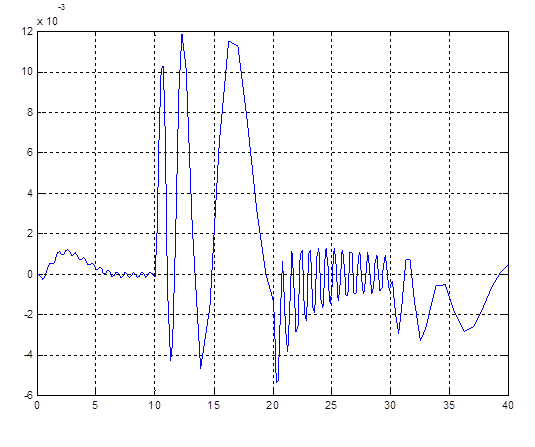
Рис. 4.18. Ошибка по x (рассогласование эталона и реальной системы)
Сравнительно с вариантом без использования пропорциональной составляющей значение ошибки уменьшилось.
Выводы
В ходе работы была построена и исследована беспоисковая адаптивная система с параллельной эталонной моделью. Использовался метод скоростного градиента. Движение в каждый момент времени противоположно градиенту скорости изменения функционала качества.
Работоспособность системы обеспечивается тем, что в процессе работы осуществляется коррекция коэффициентов регулятора, способствующая точной подстройки выходов первичного контура касательно эталонного
Построение и исследование процессов в беспоисковой адаптивной системе прямого типа
В результате работы была синтезирована и исследована беспоисковая адаптивная система, построенная на основе метода скоростного градиента. Принцип работы - коррекции коэффициентов регулятора для более точной подстройки выходов основного контура относительно эталонного.
При внесении в систему дифференциальной составляющей увеличивалось быстродействие системы, но система плохо реагирует даже на малые помехи.
Внесение пропорциональной составляющей позволяет сгладить малые колебания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.