Линейное дифференциальное уравнение второго порядка. Общая структура БАСЭМ. Симметричная и положительно определенная диагональная матрица

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ

КАФЕДРА АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Расчетное задание 5

Дисциплина: Адаптивные системы управления

Работу выполнил студент     5081/2            

группа                           ФИО

Преподаватель                          

подпись                            ФИО

Санкт-Петербург

2009г.

Задание

Рассматривается объект, математическая модель которого - линейное дифференциальное уравнение второго порядка:

Требуется:

Синтезировать и исследовать БАСЭМ.

Теоретические положения

Беспоисковые адаптивные системы с эталонной моделью относятся к классу замкнутых БАС, то есть в них для формирования алгоритма адаптации используется координатная ошибка, т.е. разность выходов основного контура и эталонной модели. Общая схема такой системы приведена на рис. 1.1.

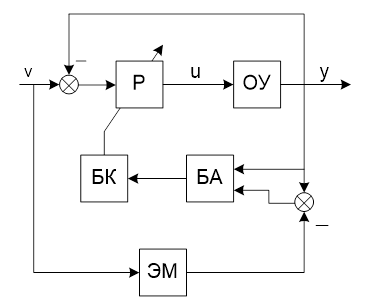
Рис. 1.1. Общая структура БАСЭМ

В данной работе исследуется метод скоростного градиента. В этом алгоритме изменение настраиваемых параметров производится в направлении, противоположном градиенту скорости изменения  функционала, характеризующего качество оптимизации.

Функционал:  – основная функция качества где      Р – симметричная и положительно определенная диагональная матрица

Р=Р^Т , Р>0.

Скорость изменения функционала:

где:     e – координатная ошибка основного контура по сравнению с эталоном

А_Э – матрица эталонного поведения системы

B – матрица управления системы

Р – обобщенный вектор сигналов

Целевая функция:

Отсюда получим закон изменения параметров регулятора:

Запишем уравнение регулятора как:

В этом случае можно записать следующие выражения для коррекции его коэффициентов:

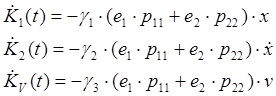
где:      - диагональные элементы матрицы Г

 - ошибка по

 - ошибка по

Исходные данные

a₀ = 5 , a₁ =                α = 1, β = 0

Получаем следующее уравнение объекта:

Результаты исследования

1. Исходная система

На рис. 2.1 приведена SIMULINK-схема исследуемой системы. Моделирование производилось при нулевых начальных состояниях системы и при периодически подаваемом на её вход единичном входном сигнале.

   

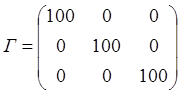
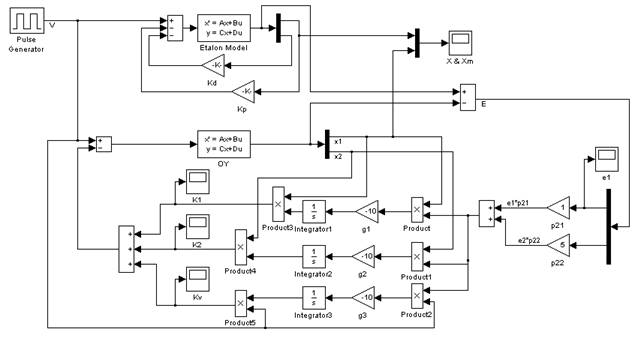
Рис. 2.1. SIMULINK-схема исследуемой системы

Рассмотрим ситуацию, при которой параметры объекта и модели совпадают. Модель включает в себя оптимальный ПД-регулятор с параметрами:

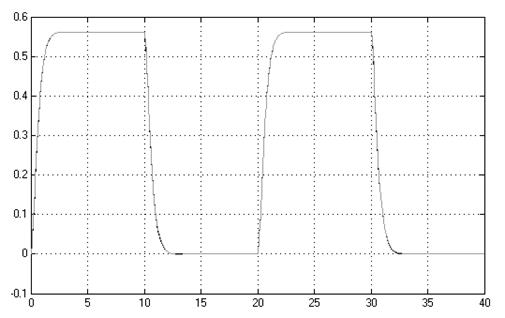
Рис. 2.2. Выходы первичного и эталонного контуров

(графики почти совпадают)

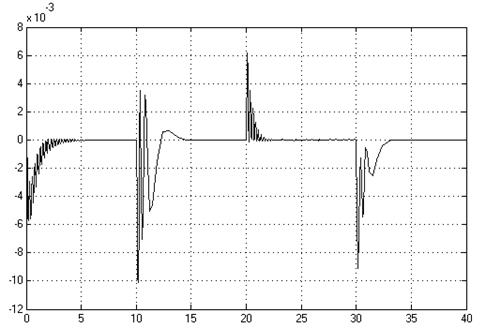
Рис. 2.3. Ошибка по х

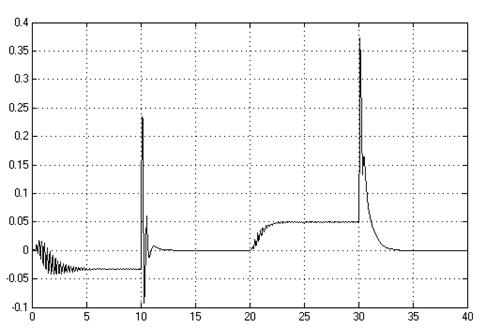
Рис. 2.4. График К₁

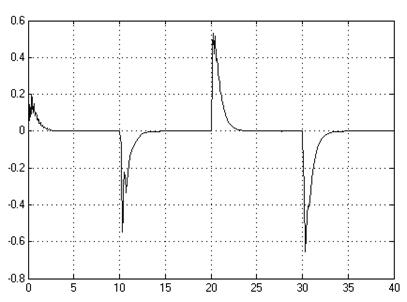
Рис. 2.5. График К₂

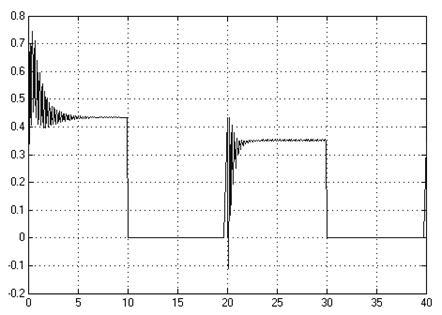
Рис. 2.6. График К_V

Внесем в систему структурные помехи, увеличив а₀ 10 раз.

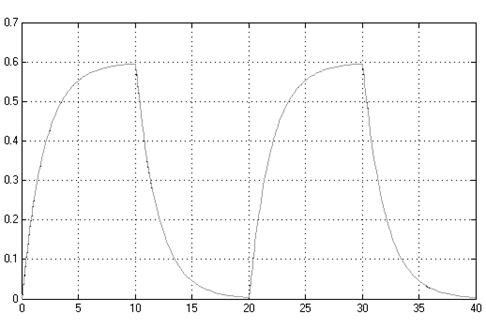
Рис. 2.7. Выходы первичного и эталонного контуров

(графики почти совпадают)

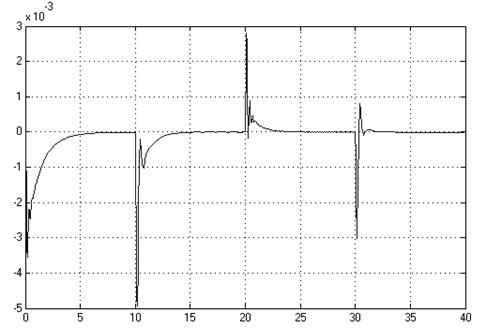
Рис. 2.8. Ошибка по х

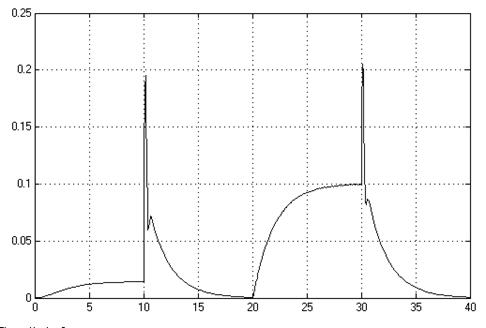
Рис. 2.9. Ошибка по х

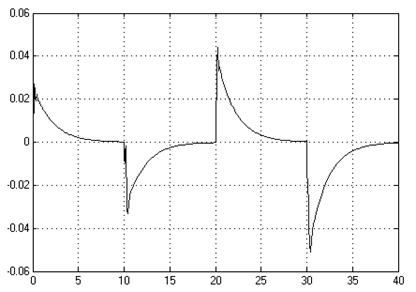
Рис. 2.10. График К₁

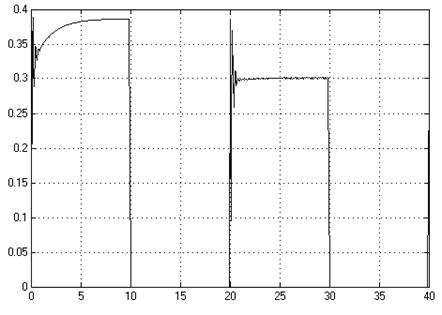
Рис. 2.11. График К₁

2. Добавление пропорционального члена

В данном случае G=- 0,5

Поскольку данная модификация ориентирована на подавление малых помех, будем исследовать систему без больших структурных помех: а₂=1.

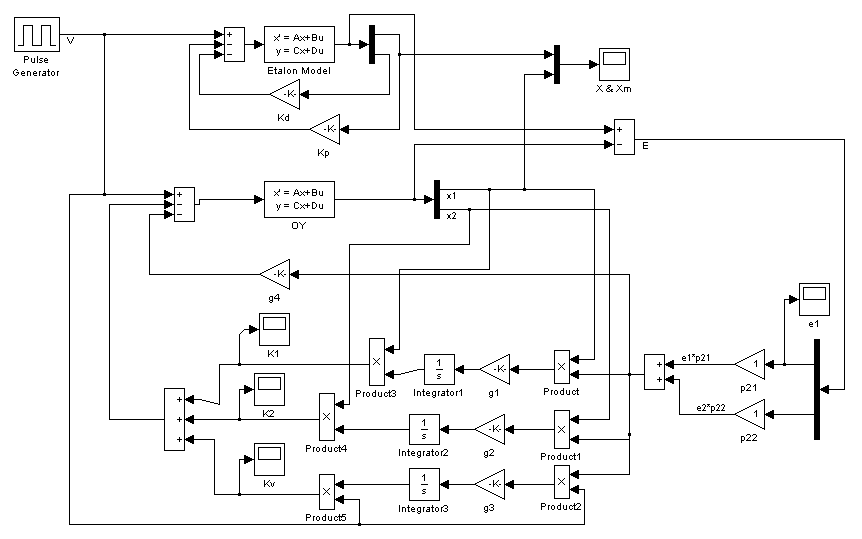
Рис. 2.12. Введение в модель пропорционального члена

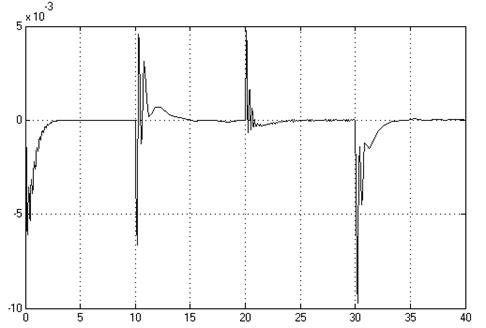
Рис. 2.13. Ошибка по x

Видно, что по сравнению с исходным вариантом значения ошибок (амплитуды «выбросов») уменьшились.

Выводы

По результатам выполненной работы можно отметить следующее.

Во-первых, система, построенная на основе метода скоростного градиента работоспособна, она осуществляет во время работы посредством коррекции коэффициентов регулятора все более и более точную подстройку выходов основного контура относительно эталонного, что можно наблюдать на примере затухающего характера ошибки по Х. При этом вносимые структурные помехи увеличивают время подстройки.

Внесение в систему адаптации дифференцирующего компонента приводит к увеличению быстродействия системы, но подчеркивает даже малые по величине помехи.

Внесение пропорционального члена дает эффект иного рода: оно позволяет сгладить небольшие по величине колебания ошибки.

Наконец, внесение элемента нечувствительности в систему позволяет сгладить «дрожание» входного сигнала системы адаптации.