Построение и исследование экстремальной СУ. Объект, описываемый линейным дифференциальным уравнением 2-го порядка

Санкт-Петербургский государственный политехнический университет

Кафедра компьютерных систем и программных технологий

Расчётное задание

Дисциплина: Адаптивные системы управления

Тема: Построение и исследование экстремальной СУ

Выполнил студент группы 5081/1        подпись                                                                                    

Преподаватель      С.  

          подпись                    

Санкт-Петербург

2011

1.  Задание

Задан объект, описываемый линейным дифференциальным уравнением 2-го порядка:

Исследовать алгоритмы идентификации параметров объекта в замкнутом и разомкнутом контурах управления. Применить следующие методы:

-  рекуррентный метод наименьших квадратов,

-  алгоритм Качмажа.

2.  Исходные данные

Меняются значения параметра a₀ (0.05, 0.5, 5).

Получим следующее уравнение:

2.  Выполнение работы

Осуществим переход к дискретной модели.

Скрипт в Matlab:

Рис. 2.1. Переходные процессы непрерывной системы и дискретных систем с различным T₀

Переход от дискретной к непрерывной системе ( R(F, G, С) -> R*(A*, B*, C*) ):

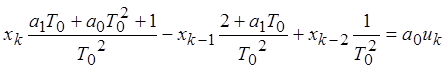
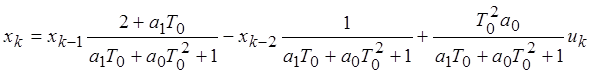
Модель системы без сигнальных помех:

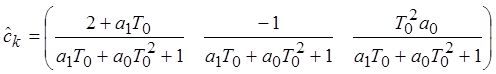
Уравнения для обратного преобразования оценочных коэффициентов в параметры системы:

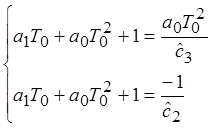
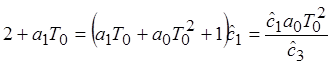
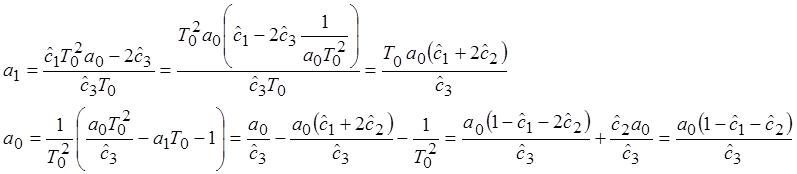
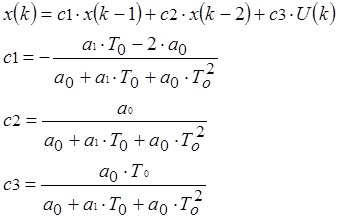
2.1.  Рекуррентный метод наименьших квадратов

Метод, сохраняя свой МНК, позволяет снизить объём хранимой информации. Работа происходит с текущими измерениями и предыдущей оценкой

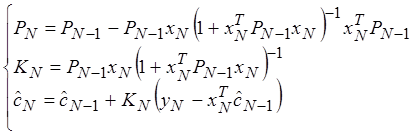
– вектор оценки неизвестных параметров после N-го измерения.

1)  Разомкнутая система

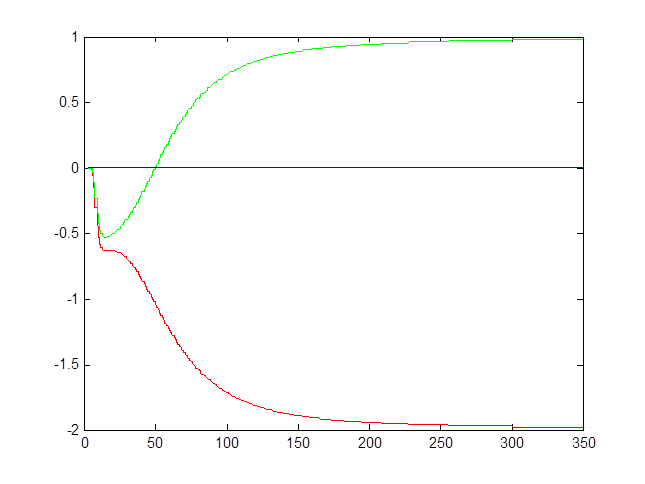
Рис. 2.2. Сходимость коэффициентов оценки параметров системы (Т₀ = 0,01 с)

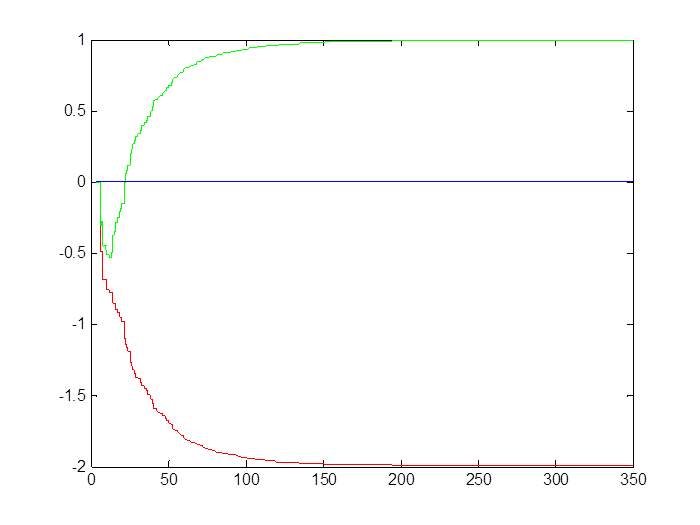
Рис. 2.3. Сходимость коэффициентов при наличии помехи (M = 0, D = 2)

Таблица 2.1. Сходимость коэффициентов оценки параметров системы

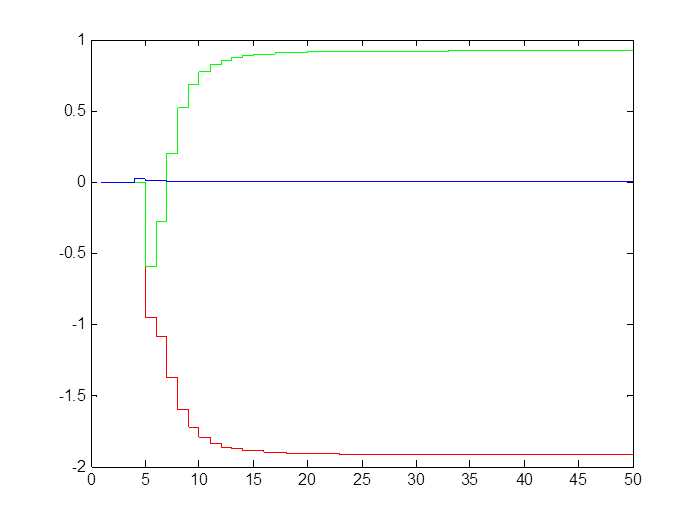
Рис. 2.4. Сходимость коэффициентов оценки параметров системы (Т₀ = 0,1 с)

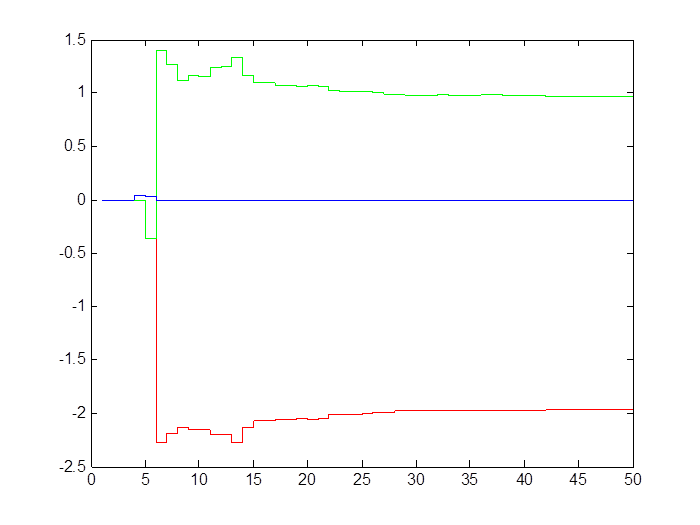
Рис. 2.5. Сходимость коэффициентов оценки при наличии помехи (M = 0, D = 2)

Таблица 2.2. Сходимость коэффициентов оценки параметров системы

2.2.  Алгоритм Качмажа

Идея состоит в решении задачи условной оптимизации, когда новая оценка строится на минимальных изменениях старой при условии выполнения требований измерений.

Формула алгоритма Качмажа:

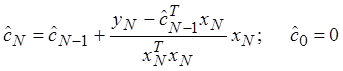
Разомкнутый контур управления.

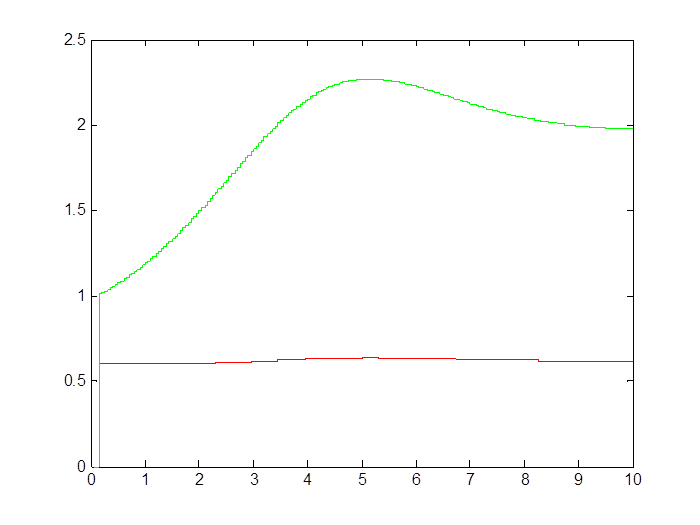
Рис. 2.6. Сходимость параметров системы (T₀ = 0,05 с)

Рис. 2.7. Сходимость параметров системы при наличии шума (T₀ = 0,05 с)

Таблица 2.3. Сходимость параметров системы

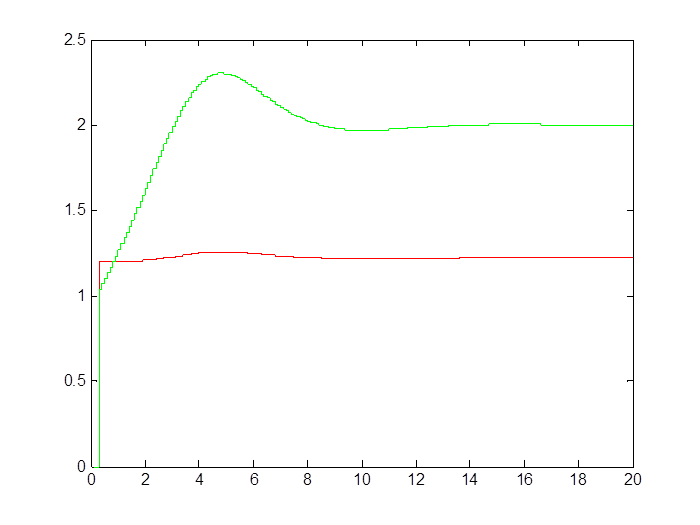
Рис. 2.8. Сходимость параметров системы (T₀ = 0,5 с)

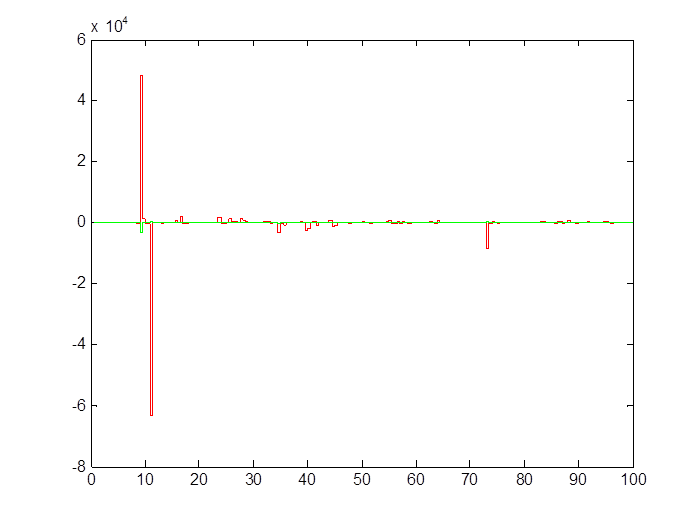
Рис. 2.9. Сходимость параметров системы при наличии шума (T₀ = 0,5 с)

Таблица 2.4. Сходимость параметров системы

Выводы

В ходе работы проводилось исследование алгоритмов идентификации параметров объекта в разомкнутом и замкнутом контурах управления. Применялись рекуррентный метод наименьших квадратов и алгоритм Качмажа.

РМНК позволяет достаточно точно получить вектор оценки параметров системы даже при наличии помех.

Решение по данному алгоритму сходится только к некоторой окрестности оценки. При действии помех сходимость в точку по алгоритму Качмажа невозможна. Для устранения недостатков этого алгоритма могут быть использованы модификации алгоритма.