Электротехника \ Адаптивные системы управления

Линейное дифференциальное уравнение второго порядка. Целевой функционал. Исследуемая система автоматического управления – поисковая (экстремальная) система

Страницы работы

12 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ

КАФЕДРА АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Расчетное задание 2

Дисциплина: Адаптивные системы управления

Работу выполнил студент 5081/2

группа ФИО

Преподаватель

подпись ФИО

Санкт-Петербург

2009г.

Задание

Рассматривается объект, математическая модель которого - линейное дифференциальное уравнение второго порядка:

Управление задано в виде: , k₁=k_п, k₂=k_д.

Задан функционал:

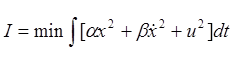
Требуется: построить систему экстремального регулирования с использованием двух методов: покоординатного спуска и градиентного.

Исходные данные

a₀ = 5 , a₁ = α = 1, β = 0

Получаем следующее уравнение объекта:

Целевой функционал

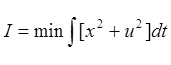
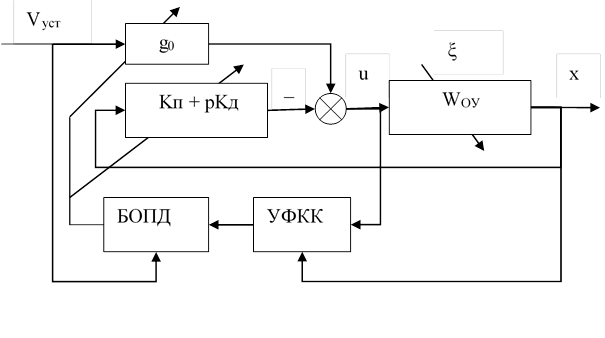
Рис. 1. Исследуемая система автоматического управления – поисковая (экстремальная) система

Передаточная функция первичного контура:

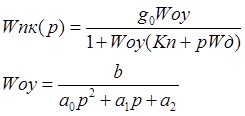
Для совпадения выхода x объекта в статике с уставкой Vуст требуется выполенение g₀= Kп+1.

Выполнение работы

1. Метод покоординатного спуска

Метод предполагает выбор направлений поиска, параллельных координатным осям. Таким образом, задача оптимизации J в двумерном пространстве раскладывается на две задачи одномерной покоординатной оптимизации, выполняемые поочередно. На каждом шаге оптимизации выполняется две итерации, на каждой из которых изменению подвергается только одна координата (K_П или К_Д).

r2.1.m

A = [0 1; -5 –sqrt(5)/2];

n = 10;

eps = 0.05;

step = -0.01;

for i = 1:n

k1 = (i-1)/10;

for j = 1:n

k2 = (j-1)/10;

sim('model');

xx(j,i) = k1;

yy(j,i) = k2;

zz(j,i) = J(length(J));

end

contour(xx, yy, zz,100)

hold on;

k1s = 1.5;

k2s = 1.5;

cnt=0;

i = 0;

while i == 0

k1 = k1s;

k2 = k2s;

sim('model');

minJ = Inf;

for k1 = k1s:step:0

sim('model');

tempJ = J(length(J));

if tempJ <= minJ

minJ = tempJ;

k1new = k1;

end

plot([k1s, k1new], [k2s, k2s]);

k1 = k1new;

k2 = k2s;

sim('model');

minJ = inf;

for k2 = k2s:step:0

sim('model');

tempJ = J(length(J));

if tempJ <= minJ

minJ = tempJ;

k2new = k2;

end

plot([k1new, k1new], [k2s, k2new]);

%проверка условия останова

if ( max(abs([k1s-k1new, k2s-k2new])) <= eps )

break;

end

k1s = k1new;

k2s = k2new;

cnt=cnt+1;

end

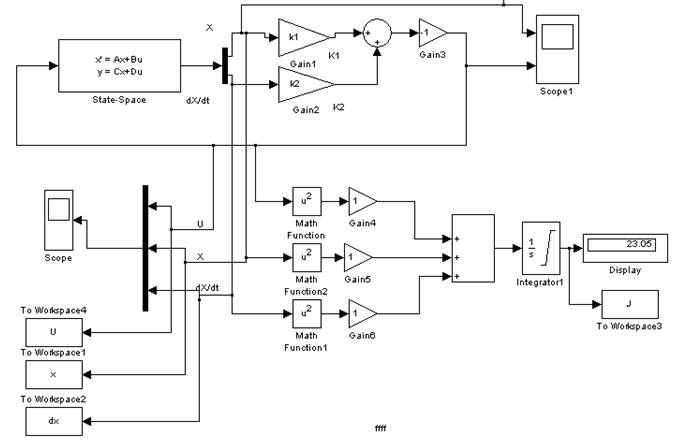
Рис. 1.1. Модель поисковой системы в Simulink

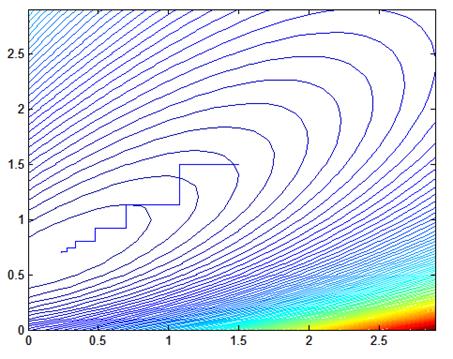
Рис. 1.2. Процесс поиска, шаг = 0.01, начальные значения Кп = 1.5, Кд = 1.5

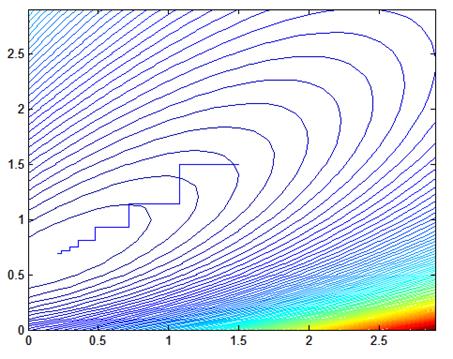
Рис. 1.3. Процесс поиска, шаг = 0.03, начальные значения Кп = 1.5, Кд = 1.5

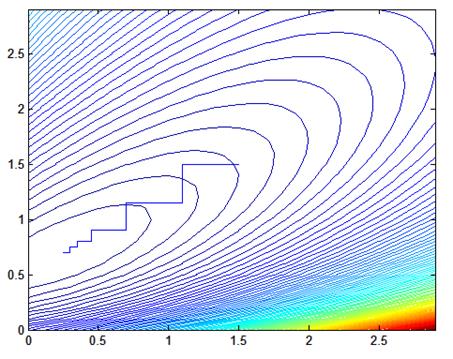
Рис. 1.4. Процесс поиска, шаг = 0.05, начальные значения Кп = 1.5, Кд = 1.5

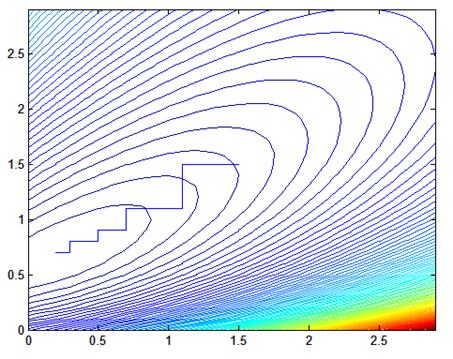
Рис. 1.5. Процесс поиска, шаг = 0.1, начальные значения Кп = 1.5, Кд = 1.5

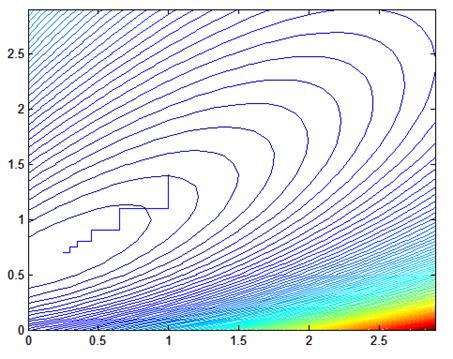
Рис. 1.6. Процесс поиска, шаг = 0.05, начальные значения Кп = 1.0, Кд = 1.4

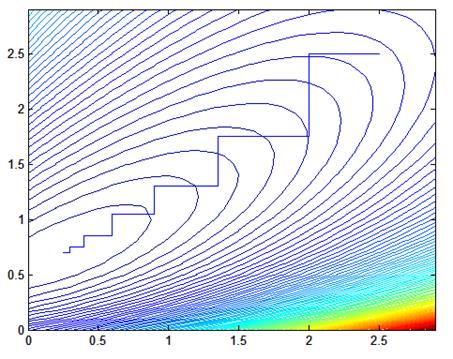
Рис. 1.7. Процесс поиска, шаг = 0.05, начальные значения Кп = 2.5, Кд = 2.5

Таблица 1.1. Результаты моделирования

Величина шага	Начальная точка		Конечная точка			Число итераций	Время поиска, с
Величина шага	К_П	К_Д	К_П	К_Д	J	Число итераций	Время поиска, с
0,05	2,5	2,5	0,3	0,7	17,16	6	27,29
0,05	1,0	1,4	0,3	0,7	17,16	5	27,29
0,10	1,5	1,5	0,2	0,7	17,16	4	26,79
0,05			0,3	0,7	17,16	5	27,29
0,03			0,24	0,69	17,15	6	26,89
0,01			0,24	0,69	17,15	6	27,19

Увеличивая шаг, мы можем уменьшить количество шагов поиска, однако при этом существенно снижается точность результата.

2. Градиентный метод

Метод основан на применении линейной аппроксимации целевой функции в каждой точке поиска. В этом случае оптимальным является градиентное направление, определенное для окрестности данной точки. Градиент определяется следующим образом: на фиксированном расстоянии от точки определяются значения целевой функции при изменении одной или другой переменной - проекции градиента. Длина шага - произведение градиента на постоянный коэффициент.

r2.2.m