Электротехника \ Адаптивные системы управления

Линейное дифференциальное уравнение второго порядка. Целевой функционал. Исследуемая система автоматического управления – поисковая (экстремальная) система, страница 2

A = [ 0 1; -5 –sqrt(5)/2 ];

n = 10;

eps = 0.05;

step = 0.05;

for i = 1:n

k1 = (i-1)/10;

for j = 1:n

k2 = (j-1)/10;

sim('model');

xx(j,i) = k1;

yy(j,i) = k2;

zz(j,i) = J(length(J));

end

end

contour(xx, yy, zz,100)

hold on;

k1s=1.5;

k2s=1.5;

delta=0.001;    % длина пробного шага

stlen = 0.1;    % длина основного шага

eps = 0.0001;

i = 0;

cnt = 0;

while i == 0

cnt=cnt+1;

k1 = k1s;

k2 = k2s;

sim('model');

Js = J(length(J));

k1 = k1s - delta;

k2 = k2s;

sim('model');

J1 = J(length(J));

k1 = k1s;

k2 = k2s - delta;;

sim('model');

J2 = J(length(J));

% Определение составляющих градиента

grad1 = (J1 - Js)/delta;

grad2 = (J2 - Js)/delta;   

% Массив градиентов на каждом шаге

G(:, cnt) = [grad1; grad2];

% Новые коэффициенты ОС

k1f = k1s + stlen*grad1;

k2f = k2s + stlen*grad2;

plot([k1s,k1f],[k2s,k2f])

% Проверка останова

if ( abs(max( stlen*grad1, stlen*grad2 )) < eps )

break;

end

% Переход в новую точку

k1s = k1f;

k2s = k2f;

end

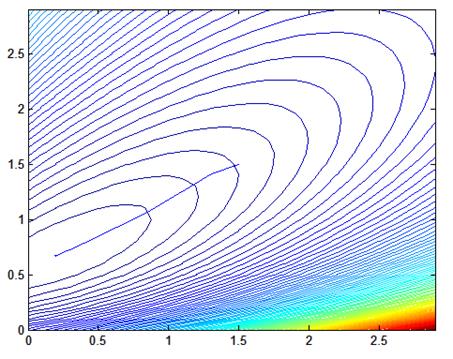
Рис. 2.1. Процесс поиска, шаг = 0.05, начальные значения Кп = 1.5, Кд = 1.5

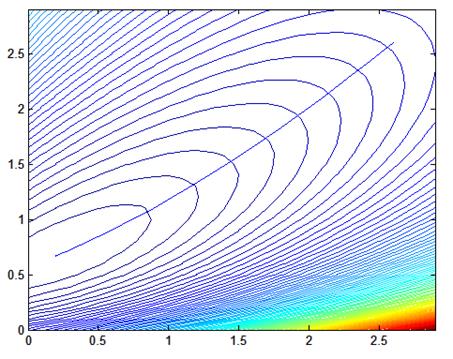
Рис. 2.2. Процесс поиска, шаг = 0.05, начальные значения Кп = 2.6, Кд = 2.6

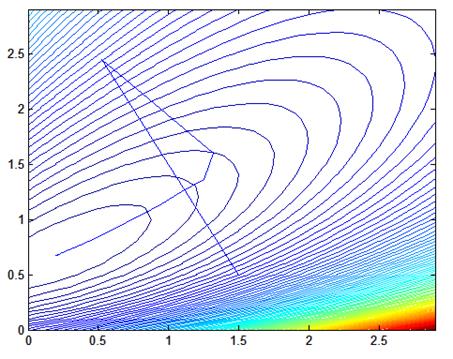
Рис. 2.3. Процесс поиска, шаг = 0.05, начальные значения Кп = 1.5, Кд = 0.5

Рис. 2.4. Процесс поиска, шаг = 0.05, начальные значения Кп = 0.2, Кд = 0.5

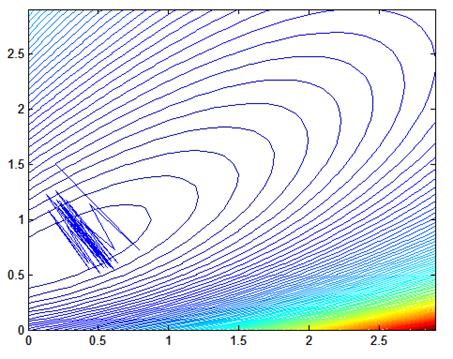
Рис. 2.5. Процесс поиска, шаг = 0.05, начальные значения Кп = 0.2, Кд = 1.5


Таблица 2.1. Результаты моделирования

Величина шага

Начальная точка

Конечная точка

Число итераций

Время поиска, с

КП

КД

КП

КД

J

0,05

2,6

2,6

0,195

0,67

17,16

60

12,61

0,05

1,5

1,5

0,21

0,69

17,16

44

12,61

0,05

1,5

0,5

0,20

0,673

17,16

54

12,61

0,05

0,2

0,5

0,41

0,89

17,16

46

12,61

0,05

0,2

1,5

0,41

0,89

17,16

34

12,61

Используя градиентный метод, можно получить большую точность.

3. Влияние дискретизации

Изменение параметров поисковых самонастраивающихся систем происходит в результате поиска экстремума заданного критерия качества, и носит дискретный характер. Одним из основных условий работоспособности системы является устойчивость первичного контура. При заданной дискретности регулятора и при заданном диапазоне изменения параметров объекта можно получить диапазон параметров регулятора, для которых первичный контур будет устойчивым.

Первичный контур описывается в переменных состояний уравнениями:

c2d(ss(A,B,C,D),0.1) -  для примера взяли T = 0.1 c

Дискретная матрица объекта:

[ 0.982-0.00391*k1, 0.089-0.00391*k2]

[  -0.089*k1-0.089,     0.9-0.089*k2]

Для устойчивости необходимо чтобы собственные числа матрицы были меньше 1, т.е. λi<1.

lmd^2 + (0.00391*k1 + 0.089*k2 - 1.9)*lmd + 0.003786*k1 - 0.089*k2 + 0.909=0

a0 = 0.00376*k1 - 0.089*k2 + 0.909

a1 = 0.00391*k1 + 0.089*k2 - 1.9

a2 = 1

Билинейное преобразование, для того чтобы применить критерий Гурвица:

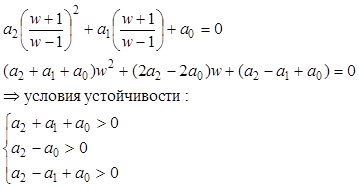
Граничные условия:

a2+a1+a0 = 0.0077*k1 + 0.009>0

a2-a0 = 0.089*k2 - 0.00376*k1 + 0.091>0

a2-a1+a0 = 3.801 - 0.18*k2 - 0.00015*k1>0

В алгоритме работы вторичного контура следует предусмотреть выполнение граничных условий для параметров регулятора.

Для исследования влияния дискретизации следует ввести фиксатор нулевого порядка в модель поисковой системы рис. 1.1.

Выводы


В данной работе мы построили систему экстремального регулирования с использованием двух методов: покоординатного спуска и градиентного.

По результатам исследований алгоритма покоординатного спуска можно отметить, что он дает сравнительно низкую точность определения коэффициентов, соответствующих минимуму ЛК-критерия качества, при значительных затратах времени. Также увеличение точности при уменьшении шага приводит к увеличению временных затрат.

Второй, рассмотренный нами метод, (градиентный) обеспечивает большую точность определения оптимальных критериев и позволяет сократить время выполнения одного шага поиска (настройки). В тоже время можно отметить увеличение числа итераций (шагов). Недостатком данного метода является зависимость от вида минимизируемой функции (присутствие/отсутствие овражности). Если «подход» к экстремуму происходит с  длинной стороны оврага, то увеличивается число мелких шагов (в ином случае можно проскочить точку, если значение градиента большое). Данный недостаток устраним путем изменения алгоритма/способа выбора длины шага.

Увеличение периода дискретизации ведет к изменению времени подстройки параметров (поиска). Изменение дискретизации связано с изменением диапазона значений параметров регулятора, в пределах которых будет происходить настройка.

Скачать файл