Построение и исследование процессов в беспоисковой адаптивной системе идентификационного типа

Санкт-Петербургский государственный политехнический университет

Кафедра компьютерных систем и программных технологий

Расчётное задание

Дисциплина: Адаптивные системы управления

Тема: Построение и исследование процессов в беспоисковой адаптивной системе идентификационного типа

Выполнил студент группы 5081/1        подпись                                                                                    

Преподаватель      С.  

          подпись                   

Санкт-Петербург

2011

1.  Задание

Задан объект, описываемый линейным дифференциальным уравнением 2-го порядка:

Построить адаптивную систему на основе идентификационного (непрямого) подхода.

2.  Исходные данные

Получим следующее уравнение:

Структура системы с адаптивным идентификатором представлена на рис. 2.

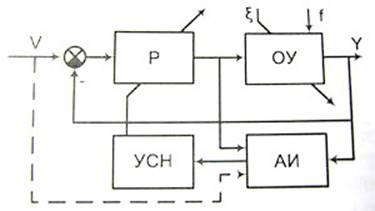
Рис. 2. Система с адаптивным идентификатором

В неявной форме существуют два процесса: процесс идентификации, минимизирующий функционал качества, и процесс вычисления изменений параметров объекта или управления на основе вторичной минимизации критерия качества или функционала качества, характеризующего управление.

3.  Выполнение работы

Идентификация параметров ОУ осуществляется посредством рекуррентного метода наименьших квадратов (РМНК), вычисление оптимальных коэффициентов ОС – по методу Риккати на основе идентифицированных параметров ОУ.

Метод РМНК, сохраняя свойства МНК, позволяет снизить объём хранимой информации. Работа происходит с текущими измерениями и предыдущей оценкой.

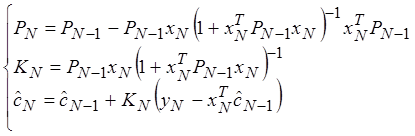
– вектор оценки неизвестных параметров после N-го измерения.

Переход от дискретной к непрерывной системе ( R(F, G, С) -> R*(A*, B*, C*) ):

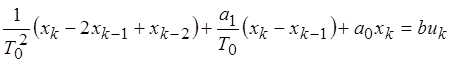
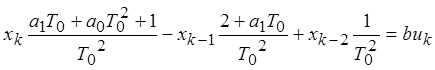
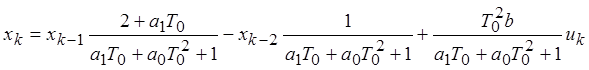
Модель системы без сигнальных помех:

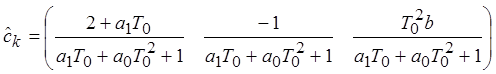
Уравнения для обратного преобразования оценочных коэффициентов в параметры системы:

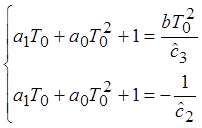
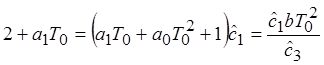
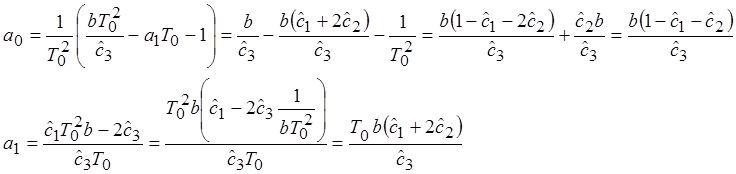
Рекуррентные формулы для вычисления оптимальных коэффициентов:

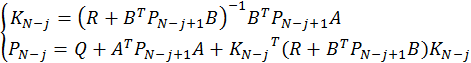
 – оптимальные коэффициенты,  – вспомогательная матрица (аналог «матрицы Рикатти»).

Начальные значения для  при j = 1: .

3.1.  Изменение параметра a₀

a₀ = 0.5 -> a₀ = 0.35

1)  Информация до изменения параметров

Оптимальные коэффициенты: k₁ = 0.8959, k₂ = 0.6180

Вычисленные коэффициент:   k₁ = 0.8502, k₂ = 0.5900

Заданный ОУ:                            a₀ = 0.5,       a₁ = 0.8

Идентифицированный ОУ:     a₀ = 0.5325, a₁ = 0.8569

,

2)  Информация после изменения параметров

Оптимальные коэффициенты: k₁ = 0.9490, k₂ = 0.7095

Вычисленные коэффициент:   k₁ = 0.9962, k₂ = 0.6995

Заданный ОУ:                            a₀ = 0.35,     a₁ = 0.8

Идентифицированный ОУ:     a₀ = 0.3650, a₁ = 0.7260

,

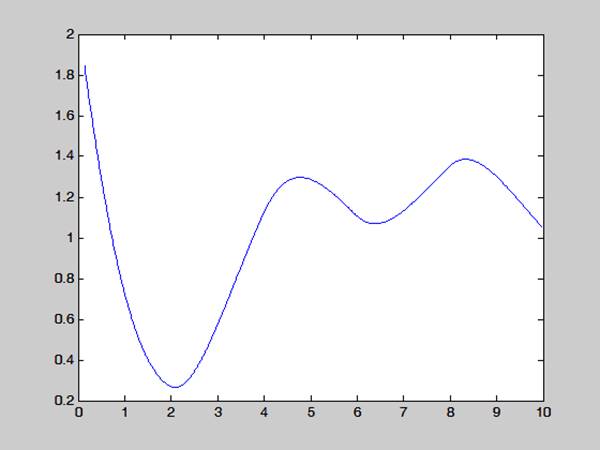
Рис. 3.1. Переходный процесс при изменении параметра а₀

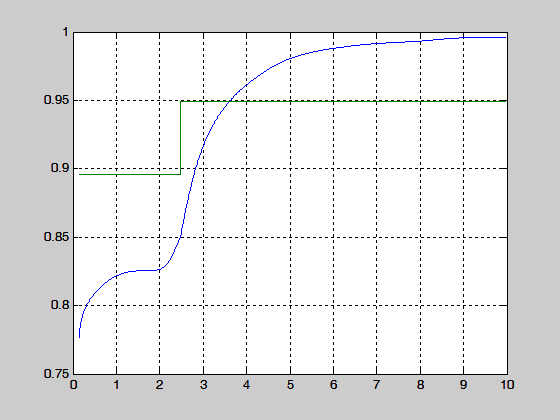
Рис. 3.2. Вычисление k₁ при изменении параметра а₀

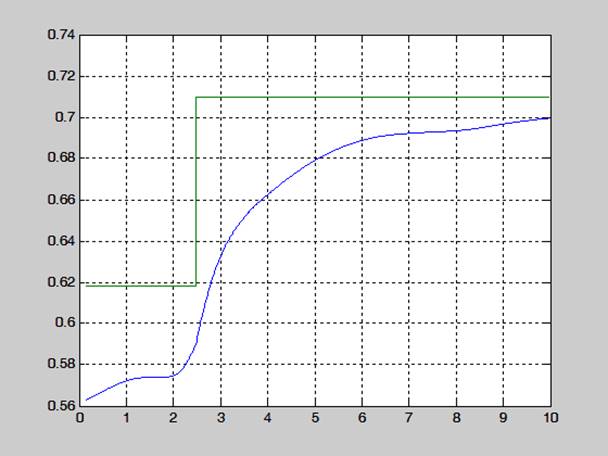
Рис. 3.3. Вычисление k₂ при изменении параметра а₀

3.2.  Изменение параметра a₁

a₁ = 0.8 -> a₁ = 0.55

1)  Информация до изменения параметров

Оптимальные коэффициенты: k₁ = 0.8959, k₂ = 0.6180

Вычисленные коэффициент:   k₁ = 0.8502, k₂ = 0.5900

Заданный ОУ:                            a₀ = 0.5,       a₁ = 0.8

Идентифицированный ОУ:     a₀ = 0.5325, a₁ = 0.8569

,

2)  Информация после изменения параметров

Оптимальные коэффициенты: k₁ = 1.0433, k₂ = 0.6180

Вычисленные коэффициент:   k₁ = 0.9493, k₂ = 0.6289

Заданный ОУ:                            a₀ = 0.5,       a₁ = 0.55

Идентифицированный ОУ:     a₀ = 0.4806, a₁ = 0.7145

,

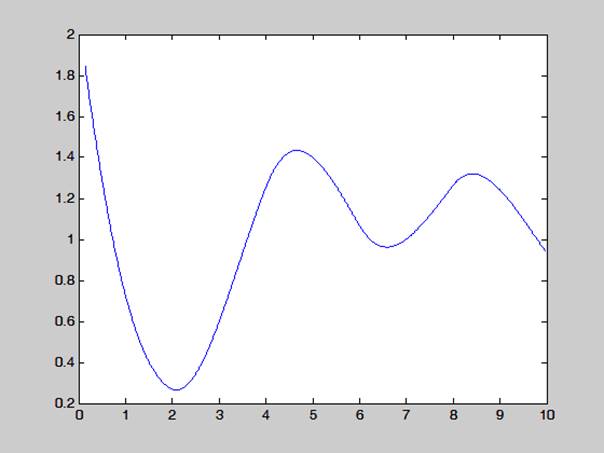
Рис. 3.4. Переходный процесс при изменении параметра а₁

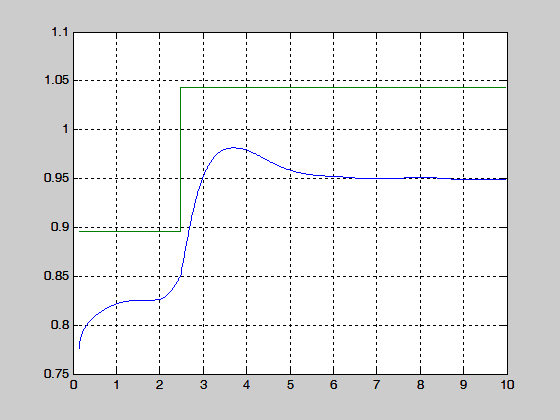
Рис. 3.5. Вычисление k₁ при изменении параметра а₁

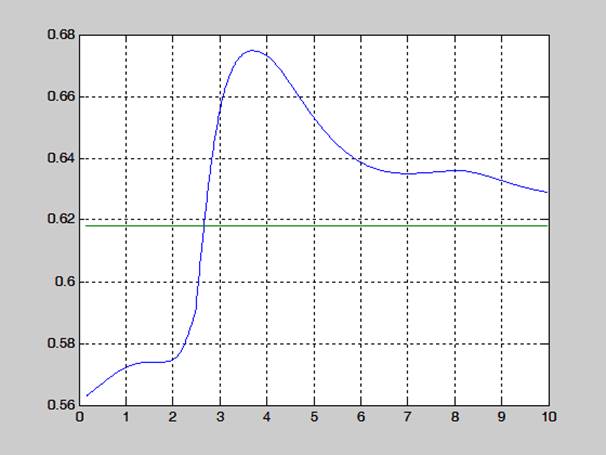
Рис. 3.6. Вычисление k₂ при изменении параметра а₁

Выводы

В ходе работы осуществлялось построение и исследование процессов в беспоисковой адаптивной системе идентификационного типа.

Метод РНМК не обеспечивает равномерной сходимости, ошибка определения может менять знак в процессе идентификации. При этом амплитуда колебаний ошибки уменьшается со временем.

Изменение a₁ больше влияет на ошибку идентификации коэффициентов регулятора и параметров объекта, нежели изменение a₀. По всей видимости, данный недостаток преодолевается за счёт увеличения количества итераций, но ввиду длительности моделирования данный эксперимент не проводился. Отсюда следует, что в условиях ограниченного времени метод РНМК является неоптимальным по точности.