Электротехника \ Адаптивные системы управления

Линейное дифференциальное уравнение второго порядка. Рекуррентный метод наименьших квадратов, страница 2

Рис. 1.3. Сходимость коэффициентов оценки параметров системы, Т0=0,1

Таблица 1.2. Сходимость коэффициентов оценки параметров системы, Т0=0,1

с1

с2

с3

Теоретические

-1,9913

0,9124

0,0402

Экспериментальные

-1,8470

0,8941

0,0660

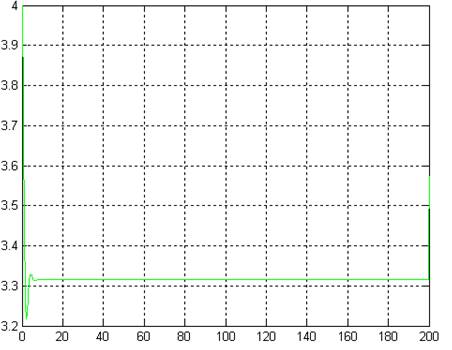
Рис. 1.4. Моделирование разомкнутой системы при отсутствии помех

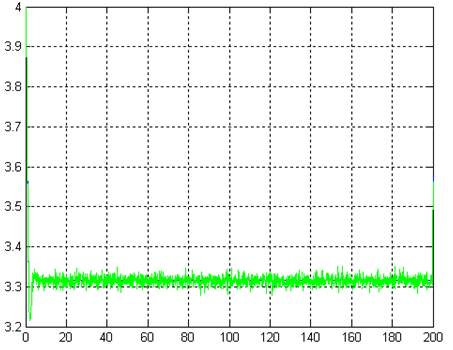
Рис. 1.5. Моделирование разомкнутой системы при наличии помех с дисперсией 0.01

Применение метода для замкнутой системы

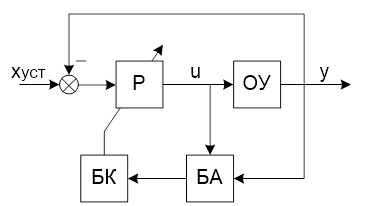
Рис. 1.6. Схема исследуемой замкнутой системы

Принцип функционирования:

1) По результатам измерения  регулируемого параметра и величины его задания вычисляются коэффициенты алгоритма и новое значение вектора оценок коэффициентов объекта;

2) На основании полученных оценок в соответствии с ЛК-критерием оптимальности вычисляются оптимальные коэффициенты ПД-регулятора.

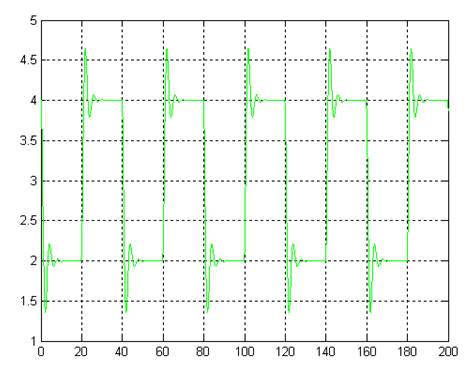
Рис. 1.7. Моделирование замкнутой системы при отсутствии помех

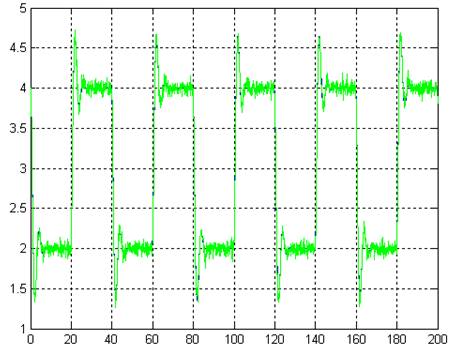
Рис. 1.8. Моделирование замкнутой системы при наличии помех с дисперсией 0.01

Вектор С = [1,9970   -0,9271   0,0183]Т – расчётное значение для T0 = 0,1 c.

Таблица 1.3. Результаты, Т0=0,1

Тип системы

Шум

РМНК

Замкнутая

0

С=[1.9694 -0.9845 0.0151]Т

0,01

С=[1.9385 0.9524 0.0140]Т

Разомкнутая

0

С=[1,9124 -0,9317 0,0080]Т

0,01

С=[1.8734 -0.8871 0.0073]Т

2. Алгоритм Качмажа

Применение метода для разомкнутой системы (рис. 1.1).

r3.3.m

clear   

T0 = 0.05;

N = 200;

A = [ 0 1; -5 –sqrt(5)/2 ];

B = [0;2];

for i=1:N              

Tk(i) = i*T0;              

end

sim('model2',Tk);

for i=1:N              

yk(i) = Yk(i);

uk(i) = Uk(i);

Tk(i) = i*T0;  

f(:,i)=[0;0;0];

Ck(:,i)=[0;0;0];

a1_ident(i)=0;

a2_ident(i)=0;

end

for k=3:N

f(:,k) = [yk(k-1); yk(k-2);uk(k)];

Ck(:,k)=Ck(:,k-1)+(yk(k)-Ck(:,k-1)'*f(:,k))/(f(:,k)'*f(:,k))*f(:,k);

a1_ident(k)=2*T0*(Ck(1,k)+2*Ck(2,k))/Ck(3,k);

a2_ident(k)=-2*(-1+Ck(2,k)+Ck(1,k))/Ck(3,k);

end

stairs(Tk,a1_ident,'r');

hold on

stairs(Tk,a2_ident,'g');

hold off

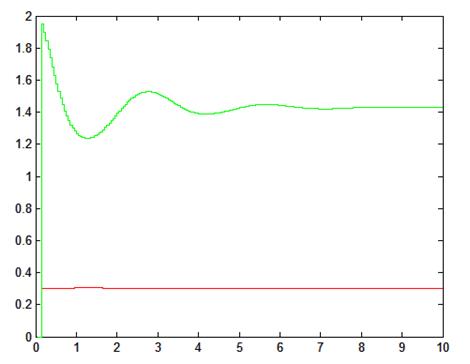
Рис. 2.1. Сходимость параметров системы, Т0=0,05

Таблица 2.1. Сходимость параметров системы, Т0=0,05

a1

a0

Теоретические

0,707

2

Экспериментальные

0,3007

1,4269

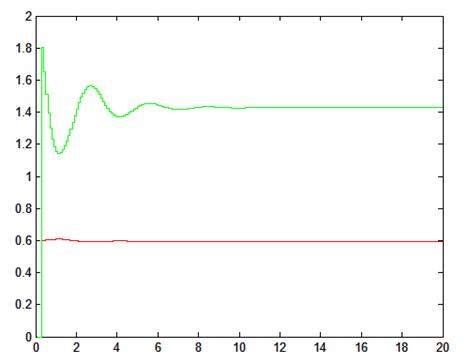
Рис. 2.2. Сходимость параметров системы, Т0=0,1

Таблица 2.2. Сходимость параметров системы, Т0=0,1

a1

a0

Теоретические

0,707

2

Экспериментальные

0,5948

1,4286

Вектор С = [1,9970   -0,9271   0,0183]Т – расчётное значение для T0 = 0,1 c.

Таблица 2.3. Результаты, Т0=0,1

Тип системы

Шум

Метод Качмажа

Замкнутая

0

С=[ 0.5074 0.5072 0.0245]Т

0,01

С=[ 0.5066 0.5065 0.0220]Т

Разомкнутая

0

С=[ 1.9073 -0.9072 0.0208]Т

0,01

С=[ 0.5058 0.5057 0.0225]Т

Выводы


В ходе выполнения работы были исследованы алгоритмы идентификации, используемые при построении адаптивных систем. Использовались два метода:

- рекуррентный метод наименьших квадратов;

- алгоритм Качмажа.

По полученным результатам можно сказать, что РМНК приводит к правильному результату в случае замкнутой или разомкнутой системы при отсутствии и наличии помех.

Метод Качмажа не обеспечивает сходимость параметров системы в точку, так как ориентируется на косвенный критерий. Он приводит к правильному результату для данного объекта только в случае разомкнутой системы и отсутствии помех.

Скачать файл