САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ
КАФЕДРА АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Расчетное задание 1
Дисциплина: Адаптивные системы управления
Работу выполнил студент 5081/2
группа ФИО
Преподаватель
подпись ФИО
Санкт-Петербург
2009г.
Задание
Рассматриваем объект, заданный линейным дифференциальным уравнением второго порядка:
Целевой функционал:
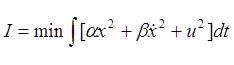
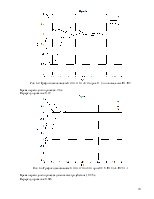
1) Синтезировать оптимальную систему линейно-квадратичного управления на основе П-регулятора в непрерывном времени. Получить аналитическое выражение уравнения Риккати. (3 режима)
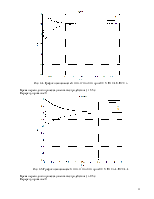
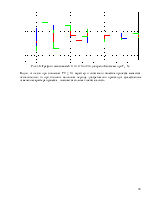
2) Исследовать зависимость значения функционала от коэффициентов K1 и K2.
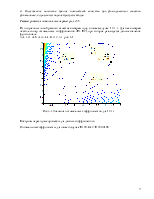
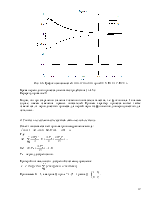
3) Исследовать изменение прямых показателей качества при фиксированном значении функционала, но различных параметрах регулятора (оценка желаемого поведения).
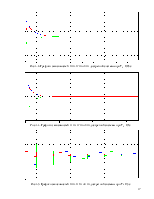
4) Исследовать влияние дискретизации на функционал и переходный процесс.
Исходные данные
a0 = 5, a1
= 
Изменяемый параметр – a0. Принимает значения 0,5; 5; 50.
α=1, β=0
Получаем следующее уравнение объекта:
Целевой функционал:
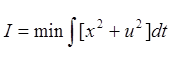
Выполнение работы
1. Синтез и исследование непрерывной оптимальной системы.
Передаточная функция объекта:
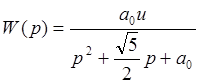
Уравнения состояния, матричный вид:
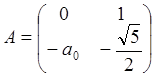
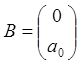
Векторно-матричное уравнение примет вид:
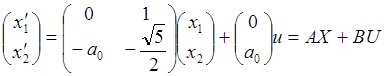
Многомерный линейный стационарный объект, описываемый векторно-матричным уравнением вида:
где
x € Rn - вектор координат управления состояния объекта
A € Rn*n - матрица параметров объекта
B € Rn*m - матрица параметров цепи управления объекта
U € Rm - вектор управления объектом
x0 - вектор начальных условий
Необходимо синтезировать управление, обеспечивающее перевод объекта из некоторого начального состояния x(t0) = x0 в заданное конечное состояние x(tf)=0 и минимизацию целевого функционала вида:
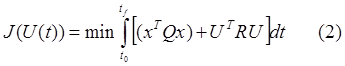
где Q и R – симметрические соответственно неотрицательно и положительно определенные диагональные матрицы (Q € Rn*n, R € Rm*m).
В теории управления решение описанной задачи известно как решение линейно-квадратичной (ЛК) проблемы оптимального управления.
Результатом ее решения является определение параметров обратной связи (регуляторов), обеспечивающей наилучший, в смысле минимального значения функционала (2) при любых начальных условиях х0.
Как известно, решение ЛК - проблемы оптимального управления для стационарных систем сводится к решению алгебраического векторно-матричного квадратного уравнения Риккати вида:
где S – квадратная положительно определенная симметрическая матрица.
В результате его решения находится оптимальное значение матрицы S* и матрицы оптимальных коэффициентов обратной связи
При этом оптимальное уравнение формируется в виде:
т. е. в форме пропорциональной обратной связи по всем координатам вектора состояния.
Таким образом, первым этапом решения ЛК – проблемы оптимального управления линейными стационарными объектами является решение алгебраического векторно-матричного уравнения Риккати.
Преобразуем нелинейное уравнение Риккати к линейному.
Для этого уравнение (4) помножим слева на R
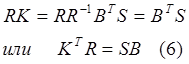
С учетом (6) уравнение (3) можно переписать в виде
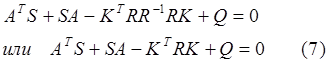
Итак, требуется решить векторно-матричную систему вида:
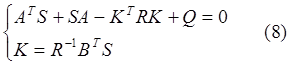
Преобразуем заданное выражение критерия к векторно-матричной форме, чтобы выполнялось следующее соответствие:
Получим:
, 
,
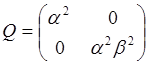Преобразуем линейное уравнение Риккати (первое в системе (8)), перенеся слагаемые, содержащие коэффициенты К, в правую часть:
Вычислим левую и правую часть, представив матрицу подстановки Риккати S в виде:
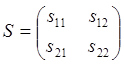. Матрица
подстановки Риккати S является симметрической, то есть 
. Обозначим диагональные
элементы матрицы S как 
. Тогда
матрица подстановки Риккати будет иметь следующий вид: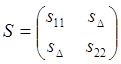 
.
Обозначим:
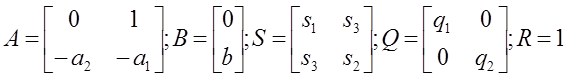
В нашем случае a2 = b ( = a0
), изменяемый параметр a0 = 0,5; 5; 50. a1 = 
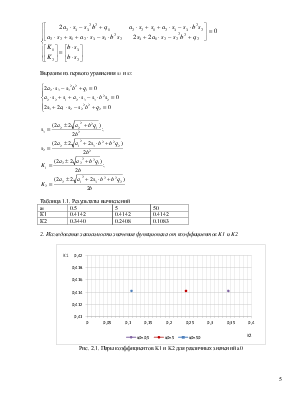
Тогда:
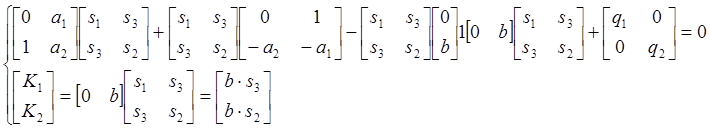
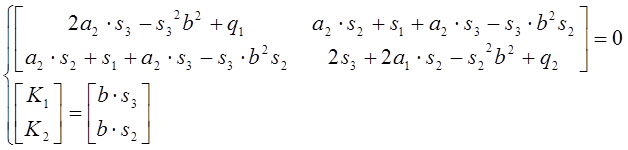
Выразим из первого уравнения s3 и s2:
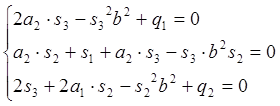
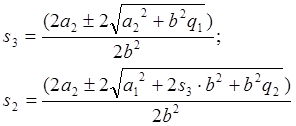
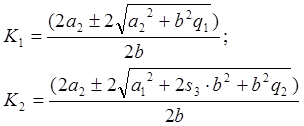
Таблица 1.1. Результаты вычислений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.