Электротехника \ Адаптивные системы управления

Изменение прямых показателей качества при фиксированном значении функционала, но различных параметрах регулятора (оценка желаемого поведения), страница 2

a0

0.5

5

50

К1

0.4142

0.4142

0.4142

К2

0.3440

0.2408

0.1083

2. Исследование зависимости значения функционала от коэффициентов K1 и K2

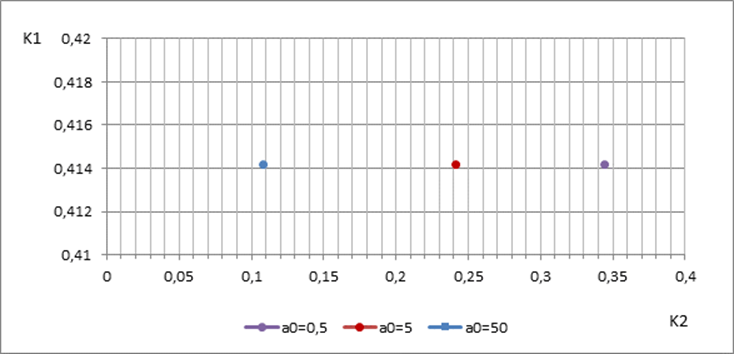Рис. 2.1. Пары коэффициентов K1 и K2 для различных значений a0


Построим линии равного уровня для критерия J в плоскости K1, K2.

ДУ 2-го порядка, описывающее поведение функционала для объекта:

r1_3_du.m

function dxj = r1_3_du(t, xj)   %функция формирования ДУ

dxj = zeros(5,1);

a0 = 5;

A = [0 1; -a0 -sqrt(5)/2];

B = [0; a0];

K1 = xj(4);

K2 = xj(5);

dxj(4) = 0;

dxj(5) = 0;

U= -[K1 K2]*xj(1:2);

dxj(1:2) = A*xj(1:2)+B*U;

dxj(3)=xj(1)^2+U^2;

Основной скрипт:

r1_3.m

[K1,K2] = meshgrid(0:.1:5);

J=zeros(length(K1),length(K2));

tspan = [0 10]; % время интегрирования

X0=[1; 0]; % начальные условия

Jn=0; % начальное значение критерия = 0

for m=1:length(K1)

for n=1:length(K2)

[t,XJ] = ode45( @r1_3_du, tspan, [X0 ; Jn; K1(1,m); K2(n,1)]);

J(m,n)=max(XJ(:,3));

end

end

mesh(K1,K2,J)

Линии равного качества строятся с помощью команды contour(K1,K2,J).


a = 5:

Рис. 2.2. Зависимость значения функционала от коэффициентов K1 и K2, а0 = 5

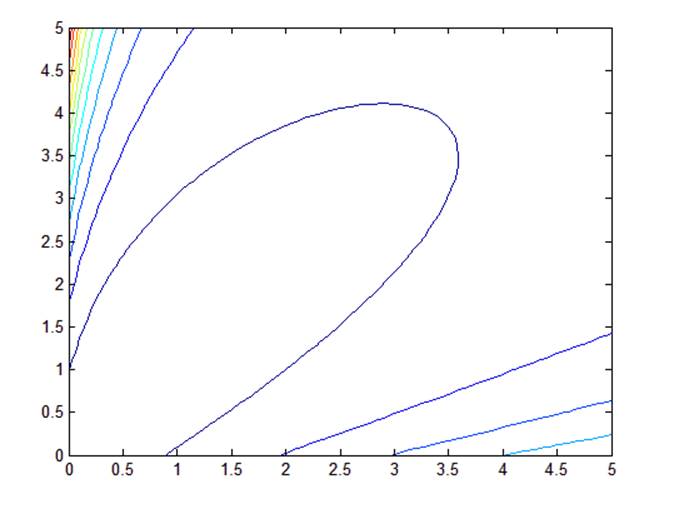
Рис. 2.3. Линии равного качества при а0 = 5


a0 = 0.5:

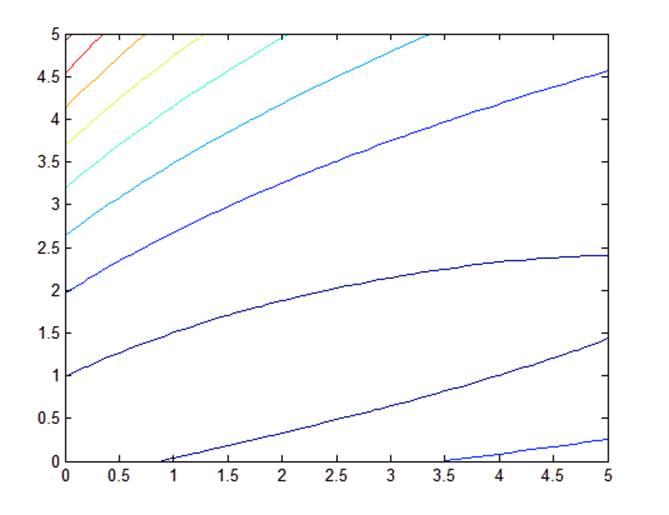
Рис. 2.4. Линии равного качества при а0 = 0,5

a0 = 50:

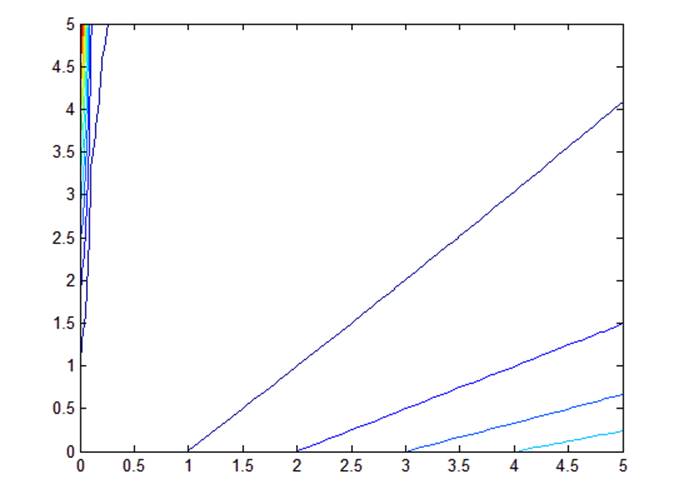
Рис. 2.5. Линии равного качества при а0 = 50


3. Исследование изменения прямых показателей качества при фиксированном значении функционала, но различных параметрах регулятора.

Рассматриваются номинальные параметры, a0 = 5.

Из полученных линий равного качества выберем одну, в нашем случае J = 1.1. Для нее выберем несколько пар оптимальных коэффициентов (K1, K2), при которых реализуется данное значение функционала:

(3.4, 1.1), (4.8, 3), (3.4, 4.4), (1.7, 3) – рис. 3.1.

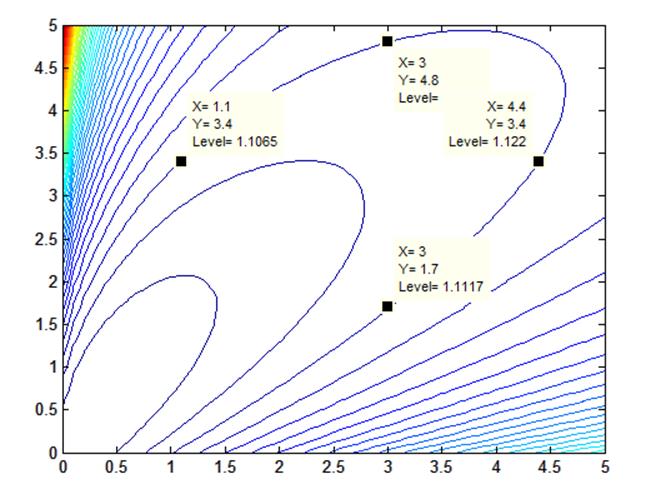
Рис. 3.1. Значения оптимальных коэффициентов для J = 1.1    

Построим переходные процессы для данных коэффициентов.

Оптимальные коэффициенты для нашего случая: K1=0.4142 ; K2=0.2408

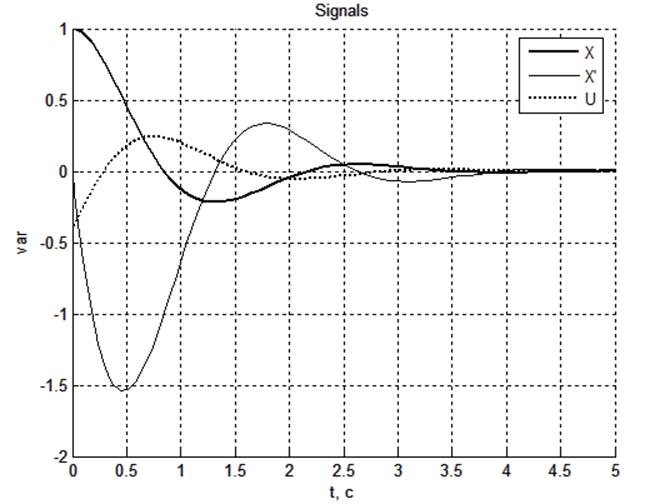
Рис. 3.2. Графики зависимостей ипри a0 = 5 и оптимальных K1, K2

Время переходного процесса: 2.6 с

Перерегулирование: 0.22

Рис. 3.3. Графики зависимостей ипри a0 = 5; K1 = 3.4, K2 = 1.1

Время переходного процесса (оценка быстродействия): 0.95 с

Перерегулирование: 0.045

Рис. 3.4. Графики зависимостей ипри a0 = 5; K1 = 4.8, K2 = 3

Время переходного процесса (оценка быстродействия): 1.55 с

Перерегулирование: 0

Рис. 3.5. Графики зависимостей ипри a0 = 5; K1 = 3.4, K2 = 4.4

Время переходного процесса (оценка быстродействия): 3.05 с

Перерегулирование: 0

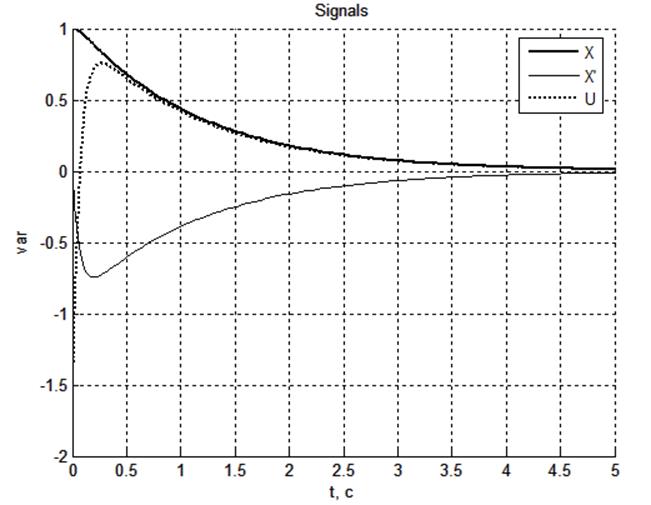
Рис. 3.6. Графики зависимостей ипри a0 = 5; K1 = 1.7, K2 = 3

Время переходного процесса (оценка быстродействия): 3.45 с

Перерегулирование: 0

Видим, что при сохранении значения косвенного показателя качества, т.е. функционала J в нашем случае, имеем изменения прямых показателей. Причем характер процесса может также изменяться, от периодического процесса для первой пары коэффициентов до апериодического для остальных.

4. Синтез и исследование дискретной оптимальной системы.

Объект описывается векторно-матричным уравнением вида:

Где

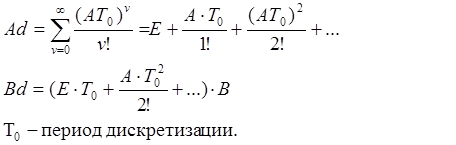
Критерий оптимальности дискретной системы управления:

             

Принимаем R = 1, а матрица Q при , равна .

Исследование влияния дискретизации формирования управляющего сигнала на значение оптимальных коэффициентов.

Расчет параметров дискретной системы.

r1_5.m

T0 = [0.001 0.005 0.01 0.05 0.1 0.5 1];

a0 = 5;

A = [0 1; -a0 -sqrt(5)/2];

B = [0; a0];

E = [1 0;0 1];

for i=1:length(T0)

Ad = 0;

Bd = E*T0(i);

for n=1:1:20

Ad=Ad+A^n*T0(i)^n/factorial(n);

Bd=Bd+A^n*T0(i)^(n+1)/factorial(n+1);

end

T0(i)

Ad = E + Ad

Bd = Bd*B

end

Таблица 4.1. Параметрические матрицы объекта при различном периоде дискретизации

Скачать файл