Электротехника \ Адаптивные системы управления

Изменение прямых показателей качества при фиксированном значении функционала, но различных параметрах регулятора (оценка желаемого поведения), страница 3

T0

Ad

Bd

0.001

1.0000    0.0010

-0.0050    0.9989

0.0000

0.0050

0.005

0.9999    0.0050

-0.0249    0.9944

0.0001

0.0249

0.01

0.9998    0.0099

-0.0497    0.9886

0.0002

0.0497

0.05

0.9939    0.0485

-0.2426    0.9396

0.0061

0.2426

0.1

0.9760    0.0938

-0.4691    0.8711

0.0240

0.4691

0.5

0.5271    0.3084

-1.5422    0.1823

0.4729

1.5422

1

-0.1978    0.2188

-1.0941   -0.4425

1.1978

1.0941

Расчет оптимального управления параметров дискретной системы.

Стационарное дискретное уравнение Риккати:

            (23)

Решением данного уравнения является значение P*, по которому можно определить оптимальные значения коэффициентов обратной связи по следующей формуле:

Аналитическое решение уравнения (22) затруднено в связи с очень громоздкой результирующей системой уравнений. Будем решать уравнение (23) итерационным способом по алгоритму:

1.  Pi = Q, i=1

2. 

3. 

4.  Если , то ,  и переход к шагу 5, иначе  и переход к шагу 2.

5.  Конец.

r1_6.m

clear all;

clc;

T0 = [0.1 0.5 1];

a0 = 0.5;

A  = [0 1; -a0 -0.8];

B  = [0; a0];

Q  = [1 0; 0 0];

R  = 1;

for i=1:length(T0)

Ad = eye(2);

Bd = eye(2)*T0(i);

for j=1:100

Ad = Ad + A^j*T0(i)^j/factorial(j);

Bd = Bd + A^j*T0(i)^(j+1)/factorial(j+1);

end

Bd    = Bd*B;

Pprev = Q;

while 1

K = ( R + Bd' * Pprev * Bd ) ^ (-1) * Bd' * Pprev * Ad;

P = Q + Ad'* Pprev *Ad - K' * ( R + Bd'* Pprev *Bd ) * K;

dP = P - Pprev;

if abs(norm( dP )) < 0.001

break;

end;

Pprev = P;

end;

P

K

end

Таблица 4.2. Значения оптимальных коэффициентов

T0

Popt

Kopt

I

0.001

1.0e+003 *

1.3359    0.0828

0.0828    0.1763

0.4108    0.8767

1.0731   

0.005

267.5920   16.5590

16.5590   35.6591

0.3984    0.8679

2.9452

0.01

134.0497    8.2850

8.2850   18.0853

0.3832    0.8569

3.5682

0.05

27.2348    1.6921

1.6921    4.0541

0.2673    0.7729

4.8236

0.1

13.9051    0.9000

0.9000    2.3345

0.1387    0.6769

5.3635

0.5

3.2774    0.4344

0.4344    1.1850

-0.3790    0.2035

6.2392

1

1.6934    0.3633

0.3633    1.2421

-0.4162   -0.0448

7.2397

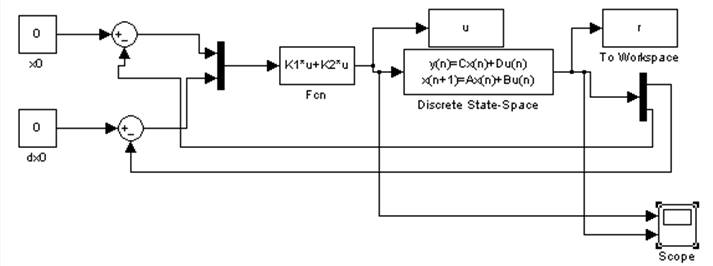
Рис. 4.1. Структурная схема модели, реализующей уравнение объекта

formAd.m

function Ad = formAd()

global T0

a0=5;

A = [0 1; -a0 -sqrt(5)/2];

E = [1 0;0 1];

Ad = 0;

for n = 1:1:20

Ad = Ad+A^n*T0^n/factorial(n);

end

Ad = E + Ad

end

formBd.m

function Bd = formBd()

global T0

a0=5;

E = [1 0;0 1];

A = [0 1; -a0 -sqrt(5)/2];

B = [0; a0];

Bd = E*T0;

for n=1:1:20

Bd = Bd+A^n*T0^(n+1)/factorial(n+1);

end

Bd = Bd*B

end

r1_7.m

T0 = 1;

a0=5;

A = [0 1; -a0 -sqrt(5)/2];

B = [0; a0];

E = eye(2);

Q = [1 0; 0 1];

R = 1;

Ad = 0;

Bd = E*T0;

for n = 1:100

Ad = Ad+A^n*T0^n/factorial(n);

Bd = Bd+A^n*T0^(n+1)/factorial(n+1);

end

Ad = E+Ad;

Bd = Bd*B;

P = Q;

cnt = 1;

eps = 1e-3;

while 1

K = ( R + Bd' * P * Bd ) ^ (-1) * Bd' * P * Ad;

Pn = Q + Ad'*P*Ad - K' * ( R + Bd'*P*Bd ) * K;

dP = Pn - P;

if abs(norm( dP )) < eps

Popt = P;

Kopt = K;

break;

end;

P = Pn;

cnt = cnt + 1;

end;

Popt

Kopt

K1 = Kopt(1)

K2 = Kopt(2)

T0

Ad = formAd()

Bd = formBd()

sim('r1_7s')

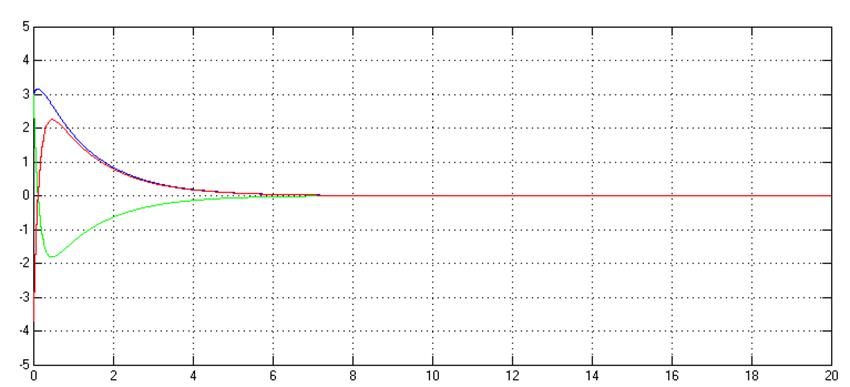
Рис. 4.2. Графики зависимостей идискретной системы при Т0=0,01с

Графики для случаев T0 = 0.001 и T0 = 0.005 визуально неотличимы от представленных на рис. 4.2.

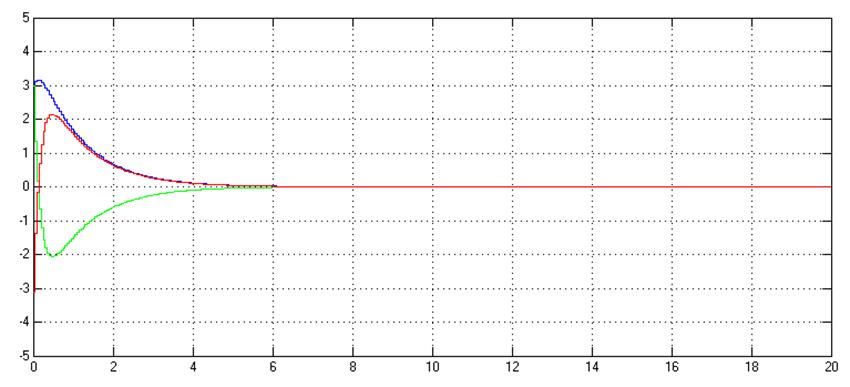
Рис. 4.3. Графики зависимостей идискретной системы при Т0=0,05с

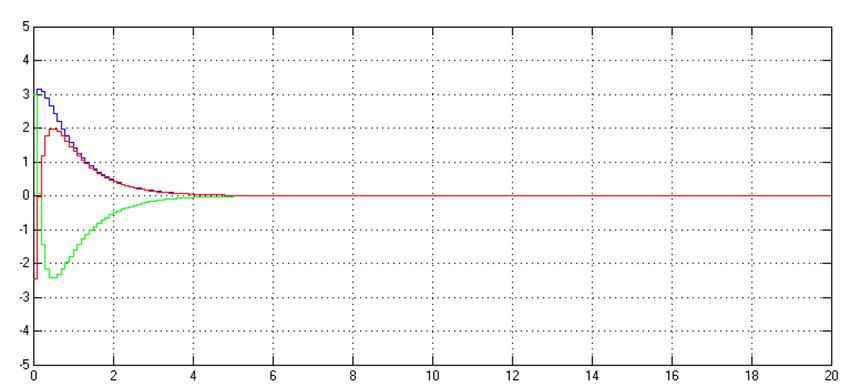
Рис. 4.4. Графики зависимостей идискретной системы при Т0=0,1с

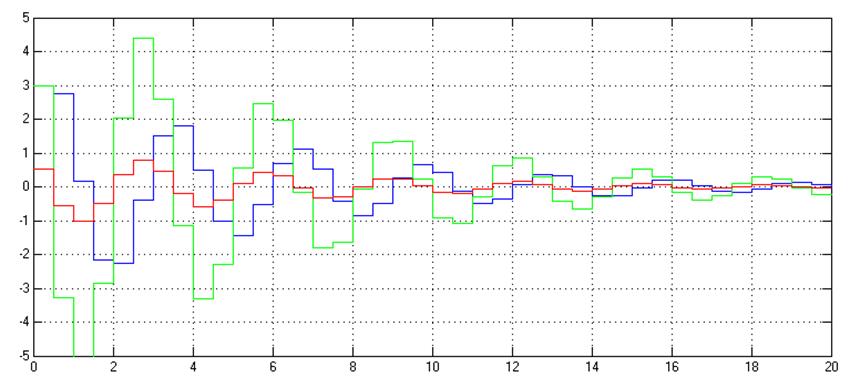
Рис.4.5. Графики зависимостей идискретной системы при Т0=0,5с

Рис. 4.6. Графики зависимостей идискретной системы при Т0=1с

Видно, что если при значениях T0 ≤ 0.1 характер и показатели качества процесса меняются незначительно, то при больших величинах периода дискретизации происходит существенное изменение характера процесса – появляется сильная колебательность.

Скачать файл