



II семестр ЛЕКЦИЯ 2
Тема 1 Методы решения задач устойчивости
1.1 Потеря устойчивости – динамический процесс.
Уточним определение устойчивого
равновесия:
Равновесие называют устойчивым, если, задавшись любой величиной η>0, всегда
можно указать такую конечную величину ε>0, что при возмущении ψ< ε,
характерное перемещение │Δ│< η.
В общем случае потеря устойчивости одного состояния равновесия системы и переход ее в новое равновесное состояние – это протекающий во времени процесс, полное описание которого требует динамического подхода.
Однако для консервативных систем статический подход при определении критических нагрузок и новых состояний системы после потери устойчивости приводит к точно таким же результатам, что и более общий – динамический.
Итак:
Статический подход: все внешние нагрузки, действующие на систему, считаются консервативными, а наложенные на систему связи – идеальными. При таких нагрузках и связях упругая система является консервативной. Условия равновесия в процессе потери устойчивости формулируются без учета инерционных сил, связанных с деформациями изучаемой системы в процессе потери устойчивости.
Динамический подход: Анализ свойств возмущенного движения, возникающего после нарушения исследуемого состояния равновесия.
Если при этом система остается в окрестности состояния равновесия, то это состояние считается устойчивым.
1.2. Статический подход: Метод Эйлера – бифуркационный критерий.
Метод Эйлера – исторически первый: изучается возможность существования форм равновесия, смежных с исходной формой.
Согласно концепции Эйлера появление смежной формы служит признаком неустойчивости.
Существо метода Эйлера состоит в том, что постановка задачи об устойчивости по отношению к заданным возмущениям подменяется иной постановкой, в известном смысле упрощенной, а именно, решается вопрос не об устойчивости в прямом смысле слова, а о существовании двух различных, но смежных, форм равновесия при одном и том же значении силы
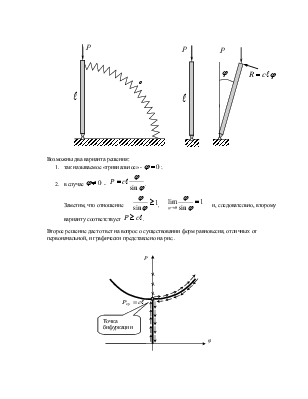
Пример:
Для системы с одной степенью свободы возможно вертикальное
положение равновесия стержня. Предположим, что наряду с вертикальной возможна и
отклоненная форма равновесия. Пружина, ось которой очерчена по окружности, при
отклонении стержня на угол ![]() создает
восстанавливающую силу
создает
восстанавливающую силу ![]() , направленную по
касательной к оси пружины. Отклоненное состояние возможно при выполнении
уравнения равновесия
, направленную по
касательной к оси пружины. Отклоненное состояние возможно при выполнении
уравнения равновесия
![]() или
или ![]() .
.
Полученное уравнение относительно параметра ![]() является
является
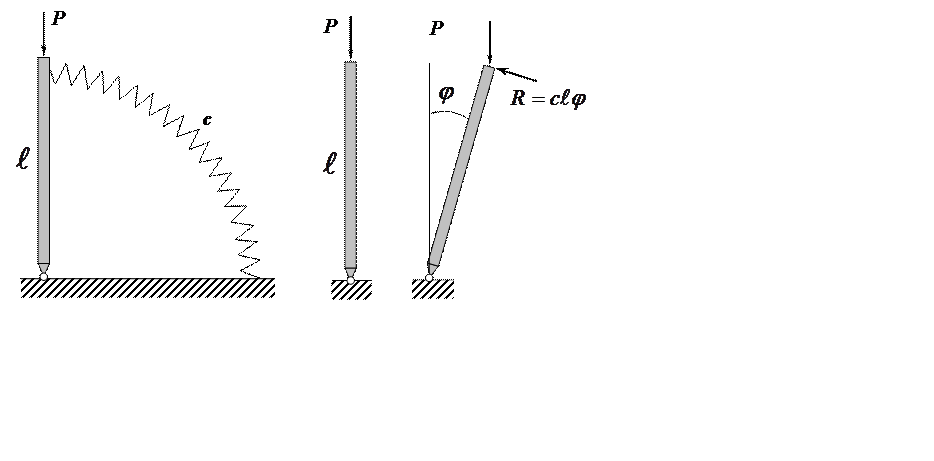
Возможны два варианта решения:
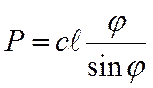 .
.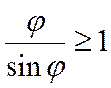 ,
, 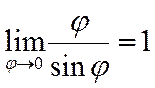 и, следовательно, второму
варианту соответствует
и, следовательно, второму
варианту соответствует Второе решение дает ответ на вопрос о существовании форм равновесия, отличных от первоначальной, и графически представлено на рис..


Т.к. в малой окрестности точки бифуркации присутствует как
первоначальная так и отклоненная формы равновесия, то для обнаружения точки
бифуркации достаточно рассмотреть сколь угодно малое отклонение ![]() , такое, что
, такое, что ![]() .
.
После замены ![]() на
на ![]() уравнение приобретает вид линейного.
Такая процедура называется линеаризацией. Решение линеаризованного уравнения
называют решением в смысле Эйлера или Эйлеровой критической силой
уравнение приобретает вид линейного.
Такая процедура называется линеаризацией. Решение линеаризованного уравнения
называют решением в смысле Эйлера или Эйлеровой критической силой
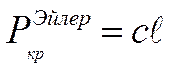 .
.
Итог:
Линейная зависимость между силами и перемещениями помимо закона Гука вытекала из предположения о малости углов поворота, которое использовалось дважды:
Записывая уравнение (), мы нарушаем оба условия. Получаем нелинейное уравнение, которое позволяет
Если мы принимаем половинчатое решение, составляя уравнения равновесия для деформированной схемы, но затем принимаем условие (), т.е. превращаем нелинейное относительно перемещения уравнение в линейное (линеаризуем задачу), то за такую непоследовательность мы расплачиваемся тем, что не можем исследовать закритическое поведение системы.
Отметим также, что в рассмотренном методе не исследовался вопрос об устойчивости или неустойчивости как первоначального, так и отклоненного положений равновесия.
Полученный результат сигнализирует об опасности, возникающей при Р=Ркр.
1.3. О влиянии неидеальностей
Выше рассматривалась идеализированная ситуация – абсолютное совпадение линии действия силы Р с осью стержня. Такое предположение характерно для метода Эйлера. В реальных условиях имеются различные несовершенства –
В этих случаях поведение нагрузки становится совершенно иным.
 Рассмотрим второй из приведенных случаев, когда в
свободном от нагрузки состоянии стержень не вертикален, а уже наклонен по
отношению к вертикали на угол φ0 . Все выводы сохраняют силу с той
разницей, что момент пропорционален углу φ-
φ0
Рассмотрим второй из приведенных случаев, когда в
свободном от нагрузки состоянии стержень не вертикален, а уже наклонен по
отношению к вертикали на угол φ0 . Все выводы сохраняют силу с той
разницей, что момент пропорционален углу φ-
φ0
![]() .
.
Наличие начального несовершенства привело к тому, что уравнение равновесия деформированного состояния неоднородно:
![]() .
.
Решение уравнения
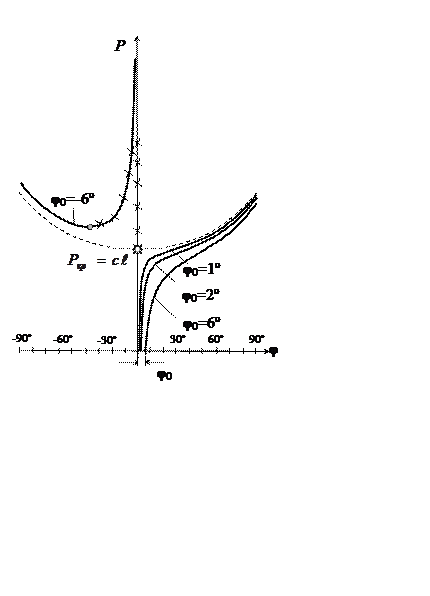
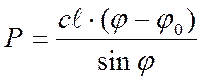 . График
этой функции:
. График
этой функции:
Отклонения от исходной конфигурации системы возникают с самого начала нагружения, само по себе отклонение, в таком случае, не может служить признаком потери устойчивости.
При плавном увеличении нагрузки реализуется правая ветвь, все точки которой, как можно показать, но не здесь, соответствуют устойчивым положениям равновесия.
Левая ветвь имеет предельную точку, разделяющую устойчивые и неустойчивые положения равновесия. Для реализации этой ветви должна быть приложена и впоследствии снята некоторая поперечная сила.
Напомним, что в рассмотренном примере внесено начальное несовершенство в систему, у которой при идеальной форме смежная форма равновесия устойчива (потеря устойчивости по Эйлеру). Как свидетельствует приведенный график, такие системы малочувствительны к несовершенствам.
Наоборот, системы, у которых при идеальной форме смежная форма равновесия неустойчива (потеря устойчивости с перескоком) заметно чувствительны к несовершенствам.
Метод неидеальностей (Циглер): Характерное перемещение системы с несовершенствами зависит и от силы и от неидеальностей. Значение силы Р, при котором характерное перемещение обращается в бесконечность называется критическим.
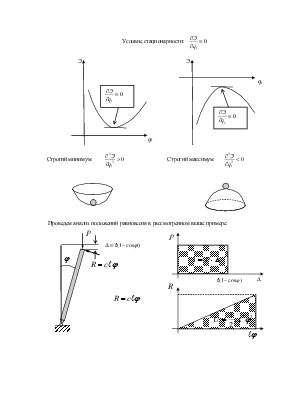
1.4. Статический подход: Энергетический критерий
Теорема Лагранжа-Дирихле: В положении равновесия полная потенциальная энергия имеет стационарное значение, причем положение устойчиво тогда и только тогда, когда это стационарное значение – строгий минимум. Это утверждение справедливо как для консервативных, так и для неконсервативных систем.
![]()
![]()
![]()
Условие
стационарности: 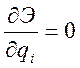

|
Строгий минимум |
Строгий максимум |
|
|
|
Проведем анализ положений равновесия в рассмотренном выше примере:
|

Условие стационарности: 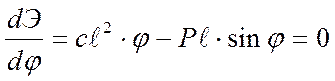 .
.
Для ответа на вопрос об устойчивости положения равновесия
вычислим вторую производную по ![]() :
: 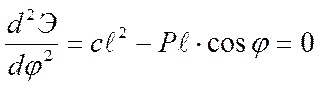 .
.
Первоначальное положение равновесия: ![]()
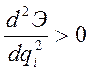 →
положение равновесия устойчиво;
→
положение равновесия устойчиво;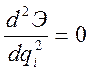 →
в таком случае анализируются производные более высоких порядков в
соответствии с теоремой:
→
в таком случае анализируются производные более высоких порядков в
соответствии с теоремой:· Если первая необращаемая в нуль производная будет нечетного порядка – то нет ни максимума ни минимума;
· Если она четного порядка и больше нуля, то имеет место минимум.
Здесь:
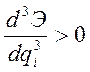 ;
; 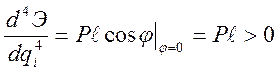
Вывод: первоначальное вертикальное положение равновесия
устойчиво при ![]() .
.
Смежное положение равновесия ![]() .
.
Учтем, что из условия равновесия 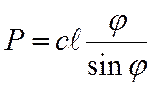 .
.
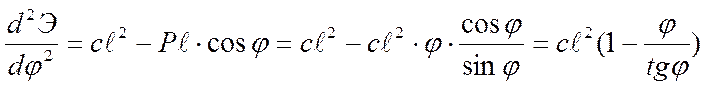 .
.
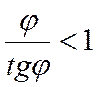 ,
, 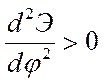 -смежное
(отклоненное) положение равновесия, реализуемое при
-смежное
(отклоненное) положение равновесия, реализуемое при 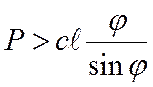 ,
устойчиво.
,
устойчиво.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.