
















Лекция 4-5-6
Спектры периодических сигналов
1. Спектральный способ описания периодических сигналов.
2. Действующие, средние значения и мощность периодических сигналов.
3. Спектры периодической последовательности прямоугольных видеоимпульсов.
4. Спектры периодической последовательности прямоугольных радиоимпульсов.
5. Связь между формой сигнала и его спектром.
1. Важнейшими формами представления сигнала являются классические способы его описания: временной, спектральный (сумма ортогональных составляющих, образующих ортонормированную систему гармоник, то есть разложение в ряд Фурье).
Справка:
любая периодическая функция V(x) с периодом 2π, удовлетворяющая в пределах периода условия Дирихле, может быть представлена следующим рядом Фурье:
![]() (1)
(1)
Исходя из этой формулы, получим систему (2):
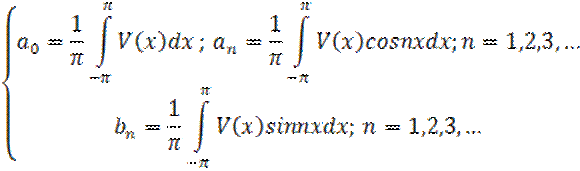
Пусть сигнал описывается временной функцией f(t) с произвольным периодом T=2π/Ώ, вводя новую переменную t=x/Ώ, приходим к функции f(x/Ώ)=V(x) с периодом ΏT=2π, разложение которой в ряд Фурье производится с помощью выражений (1) и (2).
Для f(t):
x= Ώt
dx = Ώdt = (2π/T)dt
V(x) = f(t)
Тогда функция f(t) принимает вид:
![]() (3)
(3)
Получим систему (4):
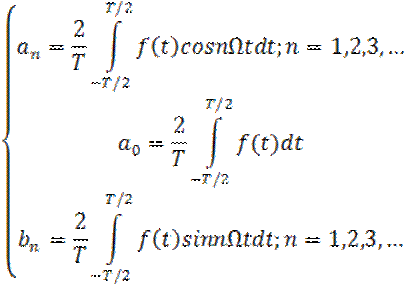
Ряд (3) может быть представлен в иной форме:
![]() (5)
(5)
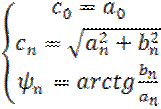 (6)
(6)
Периодический сигнал можно представить в виде наложения постоянной составляющей и бесконечного числа гармоник колебаний с частотами:
![]()
Гармонические колебания ![]() ; 2
; 2![]() ; 3
; 3![]() ;…, называется основной
или первой, второй, третьей, …, гармониками. Постоянная составляющая равна
среднему значению колебания за период.
;…, называется основной
или первой, второй, третьей, …, гармониками. Постоянная составляющая равна
среднему значению колебания за период.
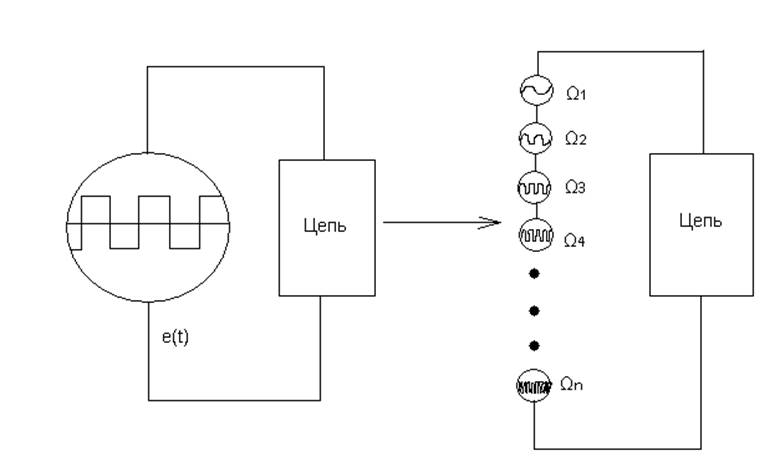
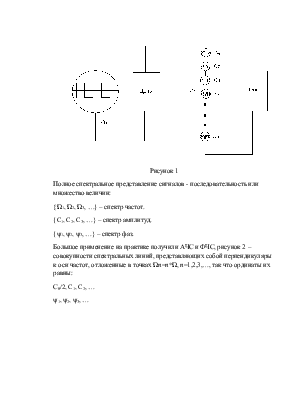
Рисунок 1
Полное спектральное представление сигналов - последовательность или множество величин:
{Ώ1, Ώ2, Ώ3, …} – спектр частот.
{C1, C2, C3, …} – спектр амплитуд.
{ψ1, ψ2, ψ3, …} – спектр фаз.
Большое применение на практике получили АЧС и ФЧС, рисунок 2 – совокупности спектральных линий, представляющих собой перпендикуляры к оси частот, отложенные в точках Ώn=n*Ώ, n=1,2,3,…, так что ординаты их равны:
С0/2, C1, C2, …
ψ1, ψ2, ψ3, …
рисунок
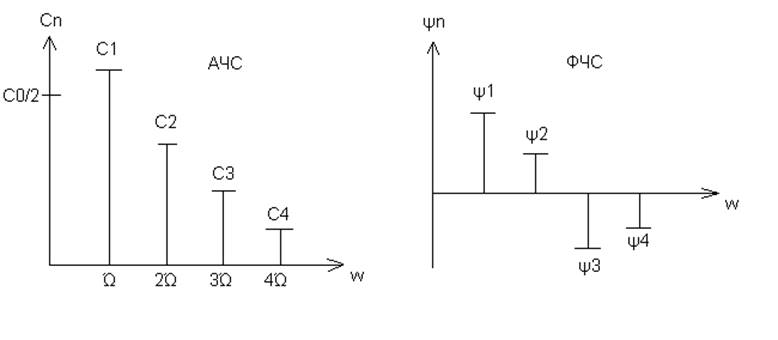
Рисунок 2
Комплексная форма записи ряда Фурье:
![]()
![]() (7)
(7)
В формуле (7) комплексные формулы определяются:
![]() (8)
(8)
В этом случае шкала частот дополняется отрицательной полуосью, АЧС становится симметричной относительно оси ординат, а ФЧС – начала координат:
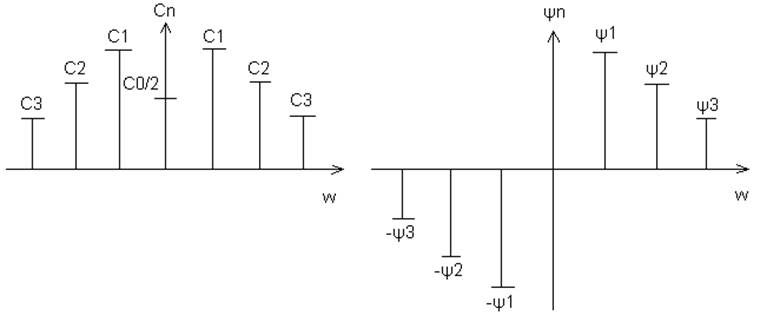
Рисунок 3
Временной и спектральный способы представления сигналов равноправны и взаимозаменяемы, это разные формы описания реально существующих процессов.
2. Действующее средне квадратическое (СК) значение периодической функции i(t).
![]() (9)
(9)
Раскладывая i(t) в ряд Фурье по формуле (5) находим:
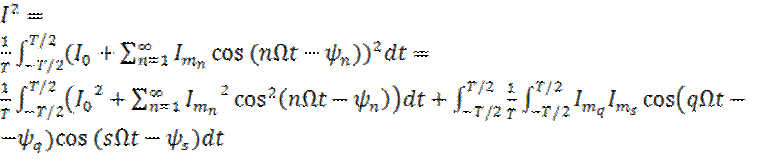 (10)
(10)
Второй интеграл при s≠q=0, так как проинтегрированные функции ортогональны. А первый интеграл представляет сумму квадратов действующего значения постоянной составляющей и всех гармоник.
![]() (11)
(11)
![]() =
=![]() (12)
(12)
Из (11) и (12) следует, что действующее значение периодического несинусоидального тока или напряжения равняется корню квадратному из суммы квадратов постоянных составляющих и квадратов действующих значений всех его гармоник.
Среднее значение периодической несинусоидальной функции равняется:
![]() (13)
(13)
Активная мощность – среднее значение мгновенной мощности.
Используя разложение U и i в ряд Фурье, получим:
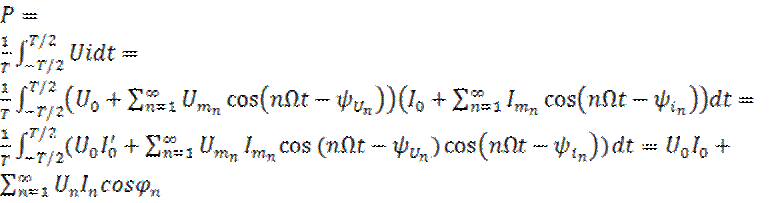 (14)
(14)
Так как:
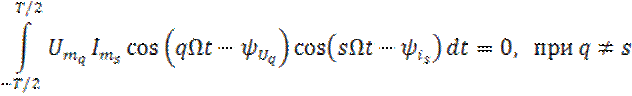
![]() (15)
(15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.