Спектры периодических сигналов. Спектральный способ описания периодических сигналов. Действующие, средние значения и мощность периодических сигналов, страница 2

Активная мощность у периодических несинусоидальных сигналов равна сумме активных мощностей постоянных составляющих и всех гармоник.

Мощность, выделяемая периодическим сигналом на r=10м:

                                                           (16)

С учетом выражений (5), (9) и (11) для периодических несинусоидальных сигналов можно получить равенство Парсеваля:

                                                      (17)

Равенство Парсеваля - выражает мощность периодического сигнала как сумму мощностей его отдельных спектральных составляющих.

 - распределение амплитуд по частоте АЧС.

 – распределение мощности сигнала по гармоникам – энергетический спектр сигнала.

Ординаты спектральных линий энергетического спектра равны квадратам действительных значений спектральных гармоник.

Диапазон частот, в котором распределены основные частоты энергии сигнала (90%), называется эффективной шириной спектра.

3. Пусть имеем сигнал U(t) показанный на рисунке (4):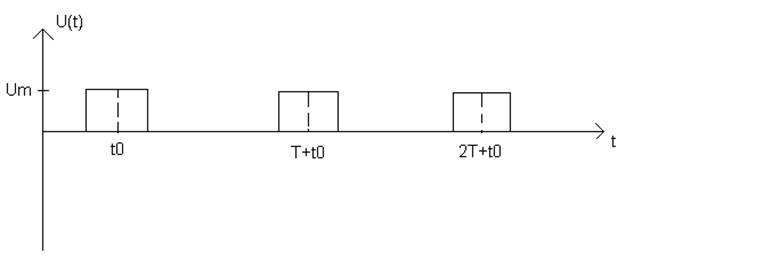

Рисунок 4

Функция U(t) в пределах периода может быть описана как:

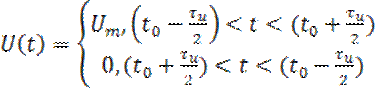                                                              (18)

Перейдем к спектральному разложению функции U(t), определяющее комплексные коэффициенты разложения функции U(t).

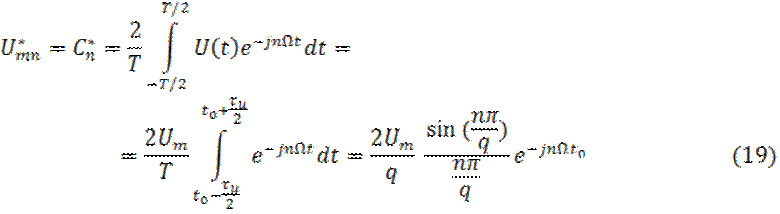
 - скважность импульса.

Величина .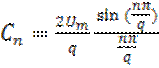

 - аргумент формулы (19) и тогда по разложению формулы (7) получаем:

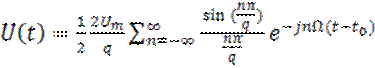                                                             (20)

Вещественная форма ряда Фурье формула (5):

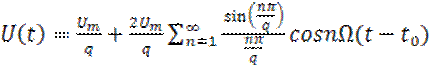                                                     (21)

 - нулевая гармоника.

 

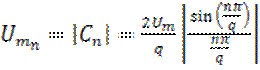
Проанализируем полученные для сигнала U(t) формулы ряда Фурье:

1) Постоянные составляющие  и амплитуды  всех гармоник пропорциональны амплитудам импульсов  и уменьшается с ростом их скважности (вызвана уменьшением средней за период энергией в импульсе).

2) Амплитуды  гармоник не зависят от сдвига импульсов во времени . Начальные фазы  не зависят от сдвига импульсов , а зависят от , .

Сдвиг сигнала во времени  определяет фазо-частотный спектр и не влияет на его АЧС.

Распределение амплитуд гармоник подчиняется закону арочного синуса , такая функция имеет арочную структуру.

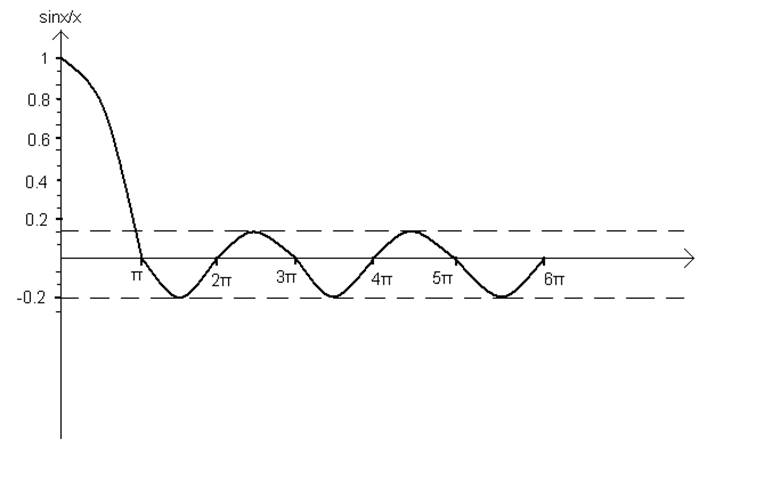
Рисунок 5

Знаки ''+'' или ''-'', перед амплитудами, соответствуют изменению от арки к арке в фазе гармоник от ''–π'' до ''+π''.

Выражение (21) можно записать иначе:

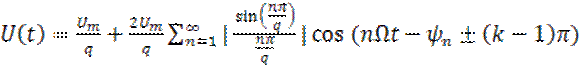                           (22)

k=1,2,3,…

Номер арки или интервалы значений переменной x равны nπ/q, при которых функция Sa(x)=sinx/x принимает определенные по знаку значения.

Анализируя спектры ФЧС и АЧС нужно учесть следующее:

1) Спектры линии находятся друг от друга на расстоянии равном частоте импульсов Ώ=2πT.

2) Распределение спектральных линий по высоте определяется огибающей спектра, характер которой зависит от формы сигнала.

3) Построение спектра: в точках nΏ на расстоянии Ώ одна от другой проводятся линии, перпендикулярные оси частот, строятся огибающие спектра, по типовым кривым или по формуле (21). Точки пересечения определяют высоту спектральных линий.

Огибающая АЧС периодической последовательности видеоимпульсов имеет такой вид:

 

Эта огибающая пересекает ось частот в точках, где x кратно π, то есть при частотах кратных скважности, поэтому гармоники с частотами  отсутствуют в спектре.

Изобразим нормированный АЧС:

 

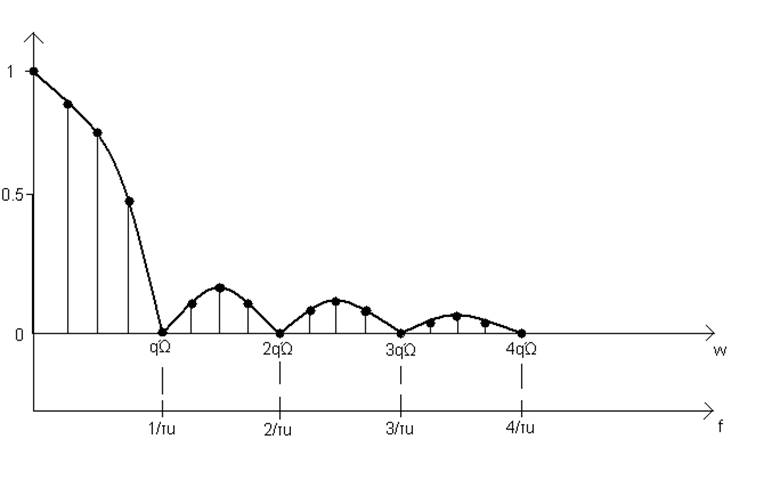
Рисунок 6

Под первыми арками сосредоточена основная часть сигнала, называется эффективной шириной спектра.

                                                                                              (23)

(23) – ширина арки.

Рассмотрим, как влияет на АЧС изменение  и .

С уменьшением  при  происходит ”сгущение” спектра: расстояние между спектральными линиями уменьшается.

Ширина спектра, определенная его огибающей, не изменяется, а основная часть энергии распределяется на большем числе гармоник.

С увеличением длительности импульса ширина арок и ширина спектра уменьшается, происходит сжатие спектра.

Основная часть энергии распределена на меньшем числе гармоник и сосредоточена на области низких частот.

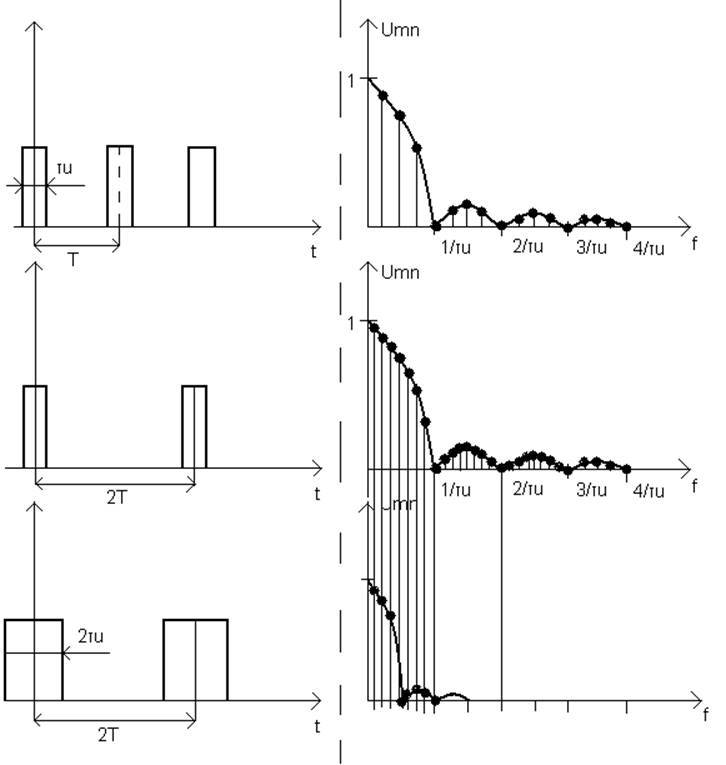
Рисунок 7

Чем короче импульсы и больше их скважность, тем гуще их спектры и наоборот.

Точность описания реального периодического сигнала оказывается достаточной, если в АЧС учитываются все гармоники, определенные в заданной ширине спектра.

ФЧС