Спектры периодических сигналов. Спектральный способ описания периодических сигналов. Действующие, средние значения и мощность периодических сигналов, страница 3

Из (21) и (22) следует, что начальные фазы гармоник определяются:

                (24)

Огибающая ФЧС – прямая с углом наклона α, который зависит от сдвига импульсов .

Учет изменения фазы гармоник на π от арки к арке осуществляется смещением прямой, параллельной себе на π вверх или на π вниз.

Каждая арка АЧС имеет ширину qΏ, поэтому величина сдвига фазы на одну арку составляет угол                                    (25)

- угол огибающей ФЧС                                                                (26)

Чем больше сдвиг во времени, тем больше наклон огибающей ФЧС.

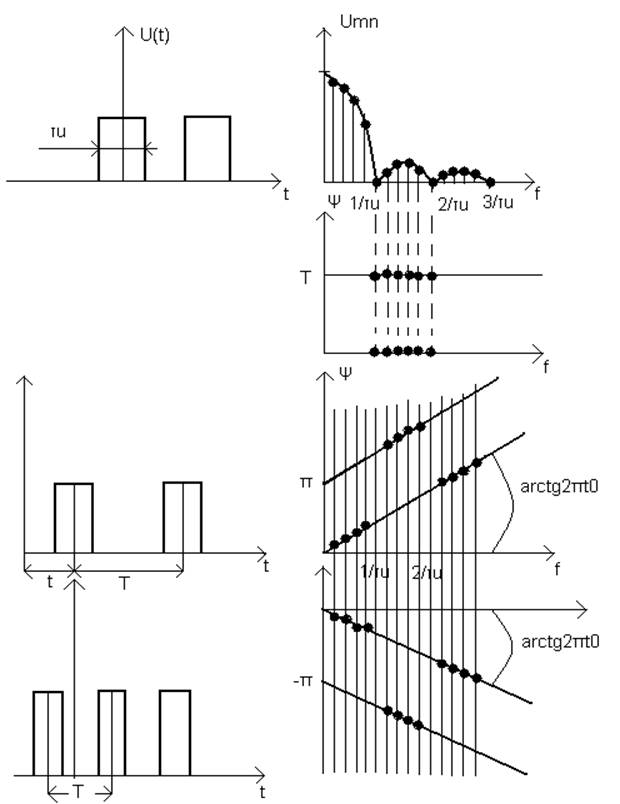
Рисунок 8

4. Дан сигнал U(t), рисунок 9:

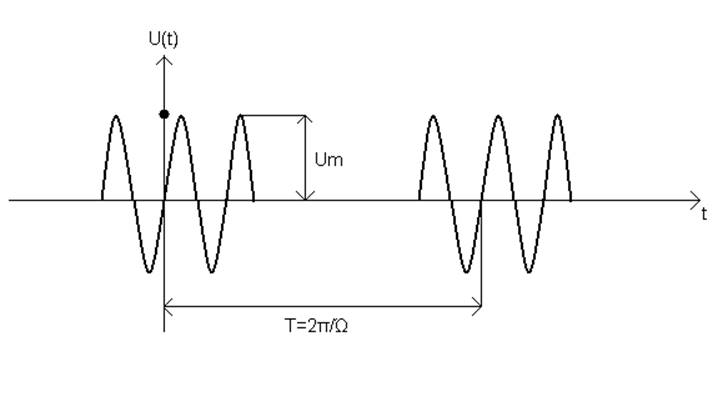
Рисунок 9

 - частота следования радиоимпульсов.

 - несущая частота высокочастотного заполнения радиоимпульса. В этом случае радиоимпульсы (рис. 9) – когерентны.

 - не когерентны.

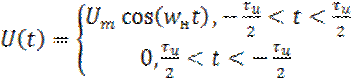                                                                  (26)

Определим постоянную составляющую:

                                               (27)

Ряд Фурье будет иметь нулевые коэффициенты =0 в силу симметрии функции U(t) относительно оси ординат.

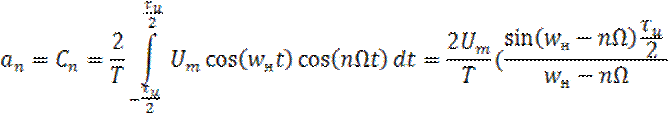
                                                                                                     (29)

Из (29) следует, что амплитуды гармоник резко возрастают в районе значений частот, близких к , но вторым слагаемым в следствии малости можно пренебречь.

Так как >>Ώ, то пренебречь можно и постоянной составляющей по формуле (28).

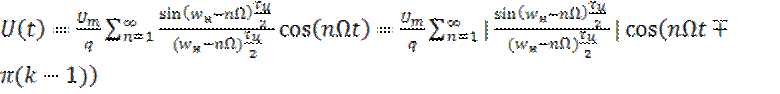                                                                                                              (30)

Из формулы (30) вытекает, что огибающая АЧС последовательности радиоимпульсов определяется Sa(x)=sinx/x, как и для видеоимпульсов.

Разница лишь в том, что эта функция:

1) Сдвинута по оси частот на величину wн.

2) Ее максимум при w=wн вдвое меньше, чем у видеоимпульсов.

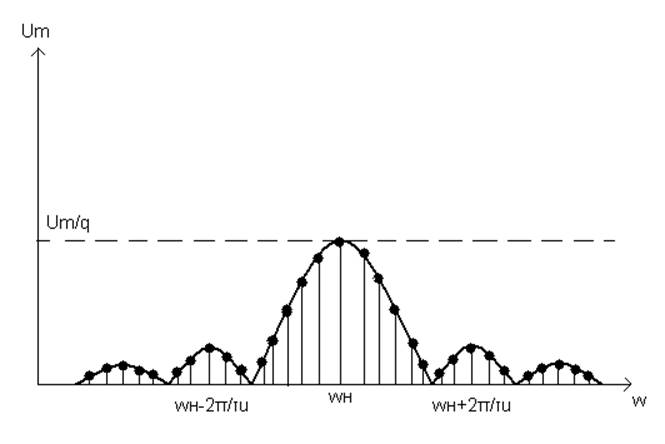
Рисунок 10

Спектр последовательности прямоугольных радиоимпульсов совпадает с видеоимпульсов, смещенных вправо по оси частот на wн. Эффективная ширина спектра радиоимпульса в 2 раза больше, чем у видеоимпульса.

В спектре некогерентной последовательности радиоимпульса несущая частота будет отсутствовать и наибольшую амплитуду имеет составляющая с частотой, близкой к wн (рис.11).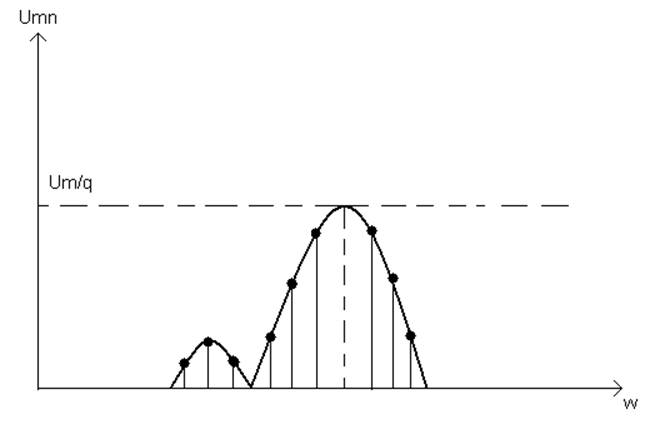

Рисунок 11

5. Форма сигнала в полной мере определяется лишь АЧС и ФЧС: имея АЧС можно судить о форме сигнала и наоборот.

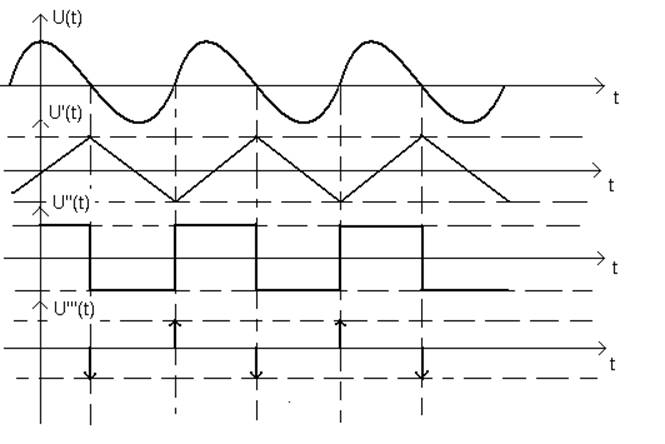
Рисунок 12

 

 

 

 

Пусть существует сигнал U(t) – временная функция. Пусть k – я производная U(t) содержит δ – функцию. Тогда для коэффициента ряда Фурье разложение U(t) справедливы такие неравенства:

                                                                                           (31)

M – постоянная, зависящая от формы сигнала.

Из рисунка 12 следует, что ряд Фурье трехугольных импульсов сходится быстрее, чем в случае прямоугольных импульсов.

Таким образом, скорость убывания амплитуд гармоник в спектре зависит от структурных свойств сигнала: коэффициенты убывают тем быстрее, чем более гладкой является форма сигнала. Если сигнал имеет скачкообразные переходы (его функция имеет конечные разрывы) и в его первой производной появляются δ – импульсы, то амплитуды гармоник уплывают медленно по закону 1/n. Если же в течении следования периода сигнал непрерывен, но в его первой производной имеются конечные разрывы, а в его второй производно2й δ – импульсы, то амплитуды гармоник уплывают быстрее по закону  и т.д. Чем быстрее убывают коэффициенты Фурье , тем более гладкая форма сигнала и меньше ширина его спектра. В пределе имеют место наиболее гладкие моногармонические колебания.

Для импульсных сигналов имеет место равенство:

 - принцип неопределенности                                                  (32)

 - ширина спектра сигнала.

 - длительность импульса.

На практике  и  определяют энергетическим методом, то есть как интервал времени или частоты, внутри которого сосредоточено 90% энергии.

Иногда желательно уменьшать длительность импульса, однако увеличивать , а значит уменьшать помехоустойчивость. А потому надо выбирать сигнал из таких соображений: . Такими сигналами являются сигналы с гладкой формой и более плавными изменениями во времени (колоколообразные импульсы).

При грубых оценках                                                                             (33)