Корреляционный анализ непрерывных сигналов (НС). Автокорреляционная функция (АКФ) сигналов и ее свойства

Лекция 11

Корреляционный анализ непрерывных сигналов (НС)

1) Автокорреляционная функция (АКФ) сигналов и ее свойства.

2) Связь между энергетическим спектром (ЭС) сигналов и его АКФ.

3) Взаимная корреляционная функция (ВКФ) и ее связь со взаимной спектральной плотностью.

1. Для количественного определения отличия сигнала U(t) и U(t-τ) принято вводить АКФ, равную скалярному произведению этих двух сигналов:

                                                                               (1)

Свойства АКФ:

1) При =0 АКФ будет равной энергии сигнала:

                                                                                                            (2)

2) АКФ есть четная функция от времени:

                                                                                                    (3)

3) При любом значении временного сдвига  модуль АКФ не превосходит энергию сигнала:

                                                                                           (4)

Доказательство неравенства Коши-Буняковского:

 

АКФ представляется симметричной кривой с центральным максимумом всегда положительным. При этом в зависимости от вида U(t) АКФ может иметь как монотонно убывающий, так и колеблющийся характер.

Примеры АКФ:

1) Видеоимпульс.

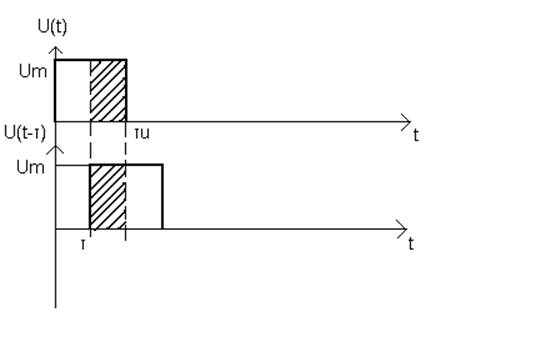
Рисунок 1

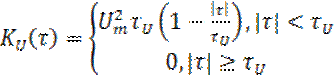                                                                       (5)

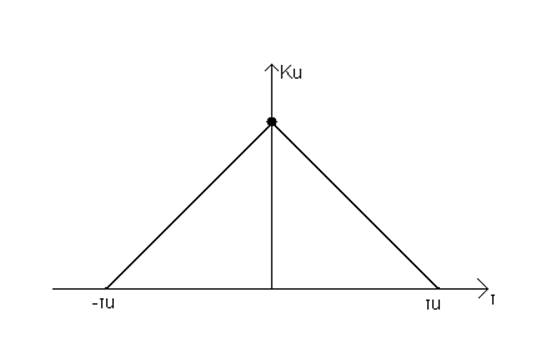
Рисунок 2

2) Радиоимпульс.

 

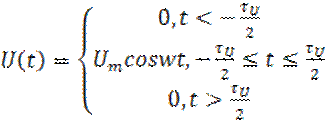
                                                     (6)

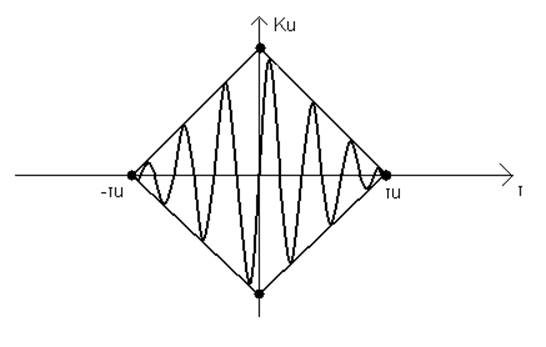
Рисунок 3

3) Серия из трех видеоимпульсов.

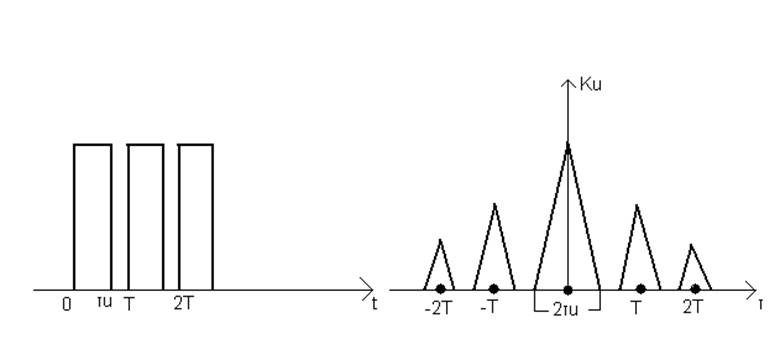
Рисунок 4

Как определить АКФ неограниченно длинного сигнала? Ведь тогда интеграл по (1) не будет сходится! Во избежание этого, новая АКФ будет определятся как среднее значение скалярного произведения и его копии.

                                                  (7)

При этом  есть средняя временная мощность взаимной мощности U(t) и его копии . Например:

дается косинусоида , . Тогда в (6) прейдем к пределу при  и получим по (7) следующее:

                                                                                                  (8)

Эта АКФ сама является косинусоидой и ее значения при τ=0  представляет собой среднюю (эффективную) мощность, которую сигнал выделяет на активной нагрузке 1 Ом.

2. Существует тесная связь между АКФ и ЭС сигнала. В соответствии с (1) АКФ есть скалярное произведение. Исходя из обобщенной формулы Релея запишем:

 

Спектральная плотность смещенного во времени сигнала:

 

 

Следовательно, АКФ U(t) будет такой:

                                                                                (9)

Квадрат  - ЭС сигнала.

Из (19) следует, что ЭС и АКФ связаны преобразованием Фурье.

                                                                             (10)

Из (9) следует и обратное соотношение:

                                                                         (11)

Выражения (9) и (11) важны по двум причинам:

1) Они дают возможность оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Принцип неопределенности (лекция 6) указывает на то, что чем в большей ширине частот распределены спектральные компоненты сигналов, тем уже основной лепесток АКФ и тем совершеннее сигнал с точки зрения возможности точного изменения момента его возникновения. (9) и (11) указывают способ экспериментального определения ЭС: часто удобнее вначале получить АКФ, а затем, используя  ППФ найти ЭС сигнала.

3. ВКФ описывает как различие формы сигналов, так и их взаимное расположение по оси времени.

По аналогии с формулой (1) ВКФ определяется для двух вещественных сигналов U(t) и V(t) по такой форме:

                                                                             (12)

Зачем нужна ВКФ? Пусть U(t) и V(t) в исходном состоянии ортогональны так, что:

 

При прохождении этих сигналов через некоторое устройство будет сдвинут на некоторый интервал τ. Значит ВКФ  служит мерой устойчивости ортогонального состояния сигналов относительно сдвигов сигналов во времени.

Свойства ВКФ:

1)  - одно и тоже взаимное положение U(t) и V(t) достигается как при сдвиге V(t) в сторону запаздывания и сдвиге U(t) в сторону опережения на одно и тоже время τ.

2) ВКФ не является четной функцией аргумента τ.

 

3)  - ВКФ ограничена и это вытекает из неравенства Коши-Буняковского.

4) При τ=0 ВКФ вовсе не обязательно достигать максимума.

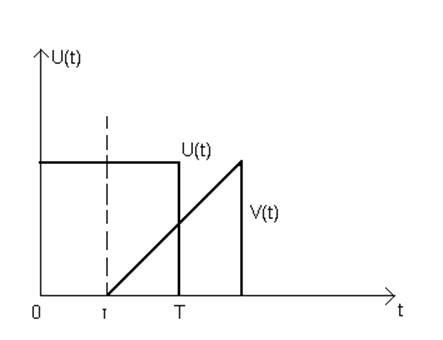
Рисунок 5

U(t)=Um

V(t)=Um t/T

Если τ>0, то η.

Если τ<0, то .

η=

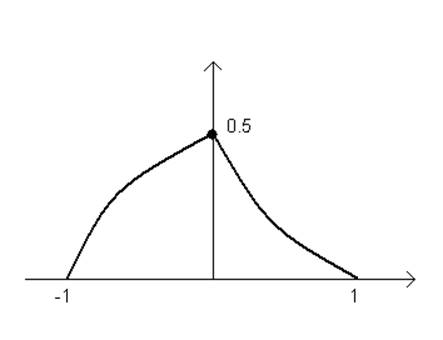
Рисунок 6

Выразим ВКФ через спектральные характеристики сигналов U(t) и V(t):

 

Поскольку спектр смещенного во времени сигнала равен:

 , то

                                                               (13)

В (13):

 - взаимная спектральная плотность сигналов         (14)

ВКФ и взаимный ЭС двух сигналов связаны парой преобразований Фурье.

                                                                      (15)