Отчет по лабораторной работе № 2
Исследование стохастических процессов
Вариант 5
Выполнила студентка 4 курс 5 группы
Цель работы: изучить стационарные и нестационарные случайные процессы.
1. синтезировать модели АМ, ЧМ- и ФМ-сигналов со случайными параметрами модуляции. Вычислить спектральные характеристики.
2. синтезировать равновероятный шум. Построить гистограмму распределения. Вычислить спектральные характеристики.
3. синтезировать «белый» гауссовский шум. Построить гистограмму распределения. Вычислить спектральные характеристики.
4. Синтезировать смесь гармонического сигнала и шума. Задать отношение сигнал/шум [-40,-20,0,+20 dB]. Построить гистограмму распределения. Вычислить спектральные характеристики в линейном и логарифмическом масштабах.
Ход работы
Модуляция: Амплитудная
fd=2200; частота дискретизации
t=0:1/fd:1; выборка по времени
n=length(t); длина выборки
df=fd/n; разрешение по частоте
fs=600; частота сигнала
fm=50; модулирующая частота
1.Генерация модулированных сигналов
1) Амплитудная модуляция
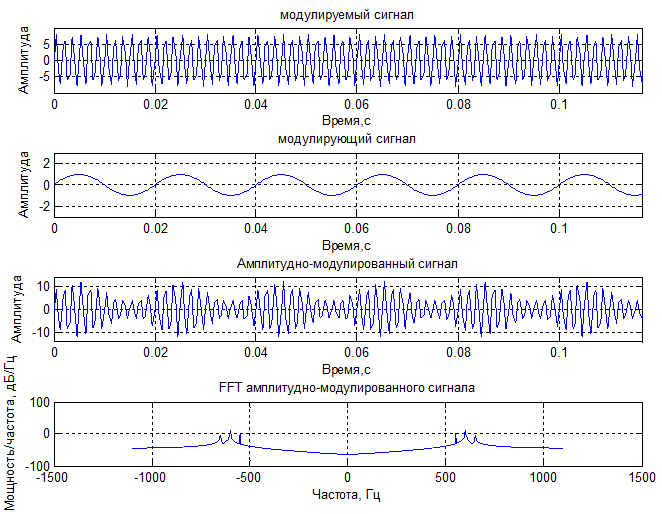
Суммарная мощность процесса ( σ2 + m2) = 36.2198
Mощность процесса по спектральным оценкам = 36.1845
2) Фазовая модуляция:
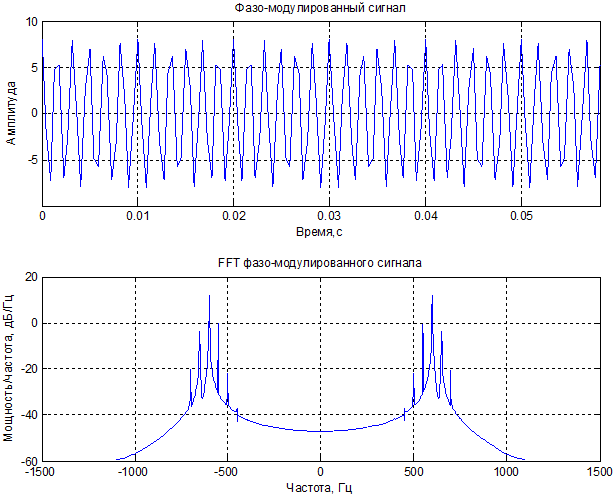
Суммарная мощность процесса ( σ2 + m2) = 32.0535
Mощность процесса по спектральным оценкам = 32.0222
3) Частотная модуляция:
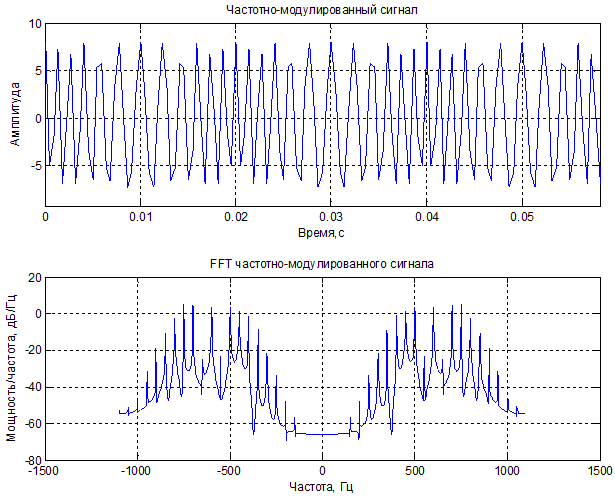
Суммарная мощность процесса ( σ2 + m2) = 32.0496
Mощность процесса по спектральным оценкам = 32.0183
4) Частичная реализация частотно-модулированного сигнала:
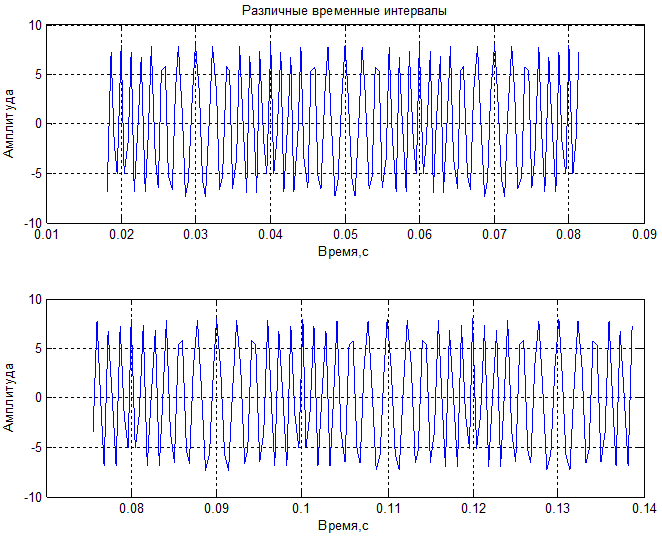
Спектральная плотность мощности частичных реализаций:
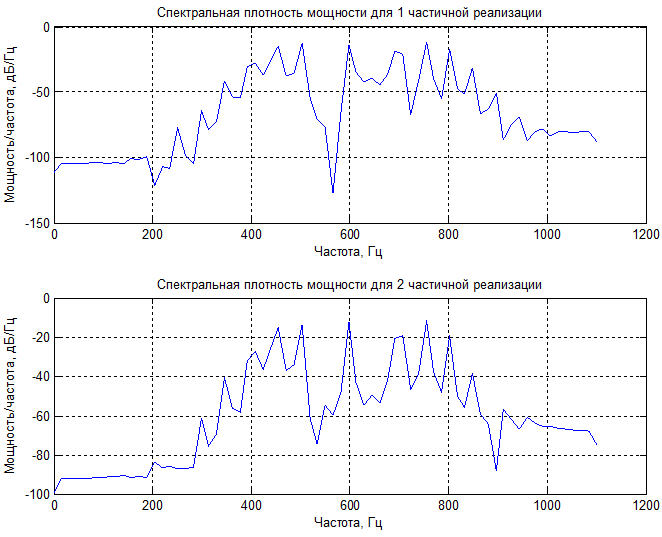
Суммарная мощность 1-й частичной реализации процесса ( σ2 + m2) = 32.3646
Mощность 1-й частичной реализации процесса по спектральным оценкам = 32.1334
Суммарная мощность 2-й частичной реализации процесса ( σ2 + m2) = 32.3198
Mощность 2-й частичной реализации процесса по спектральным оценкам = 32.0890
2. Генерация шумов
1) Равновероятный
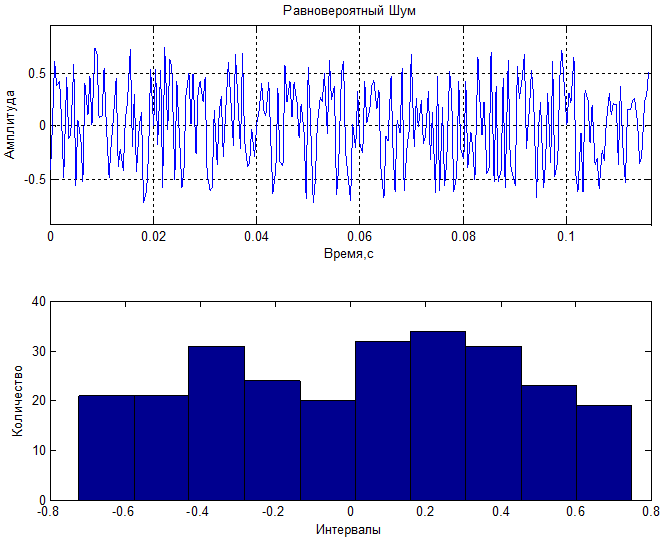
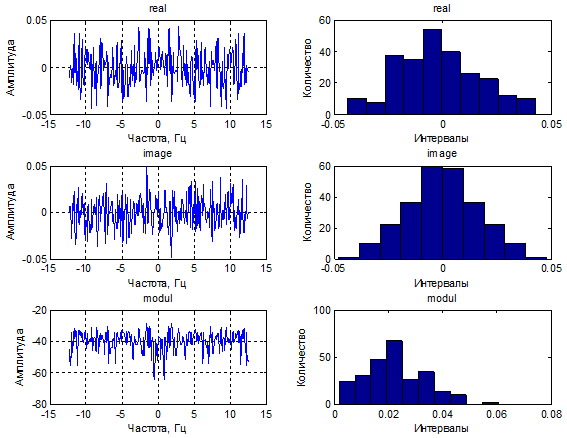
Комплексный спектр, амплитудный спектр и спектр мощности по отдельной реализации. Гистограммы распределения полученных спектральных компонент:
Сравнение СПМ центрированного и нецентрированного шума:
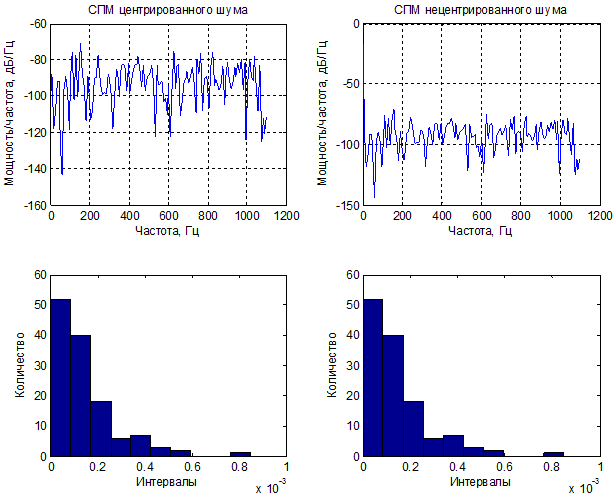
Суммарная мощность нецентрированного процесса ( σ2 + m2) = 1.6010
Mощность нецентрированного процесса по спектральным оценкам = 1.6004
Суммарная мощность центрированного процесса ( σ2 + m2) = 0.1615
Mощность центрированного процесса по спектральным оценкам = 0.1608
2) Гауссов
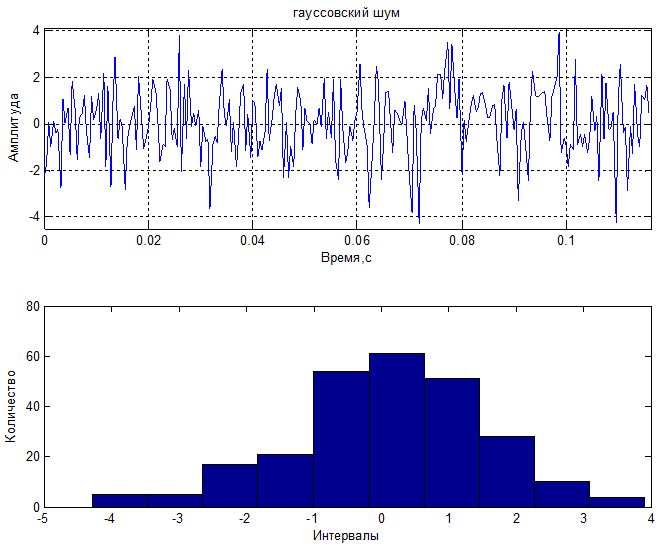
Комплексный спектр, амплитудный спектр и спектр мощности по отдельной реализации. Гистограммы распределения полученных спектральных компонент:
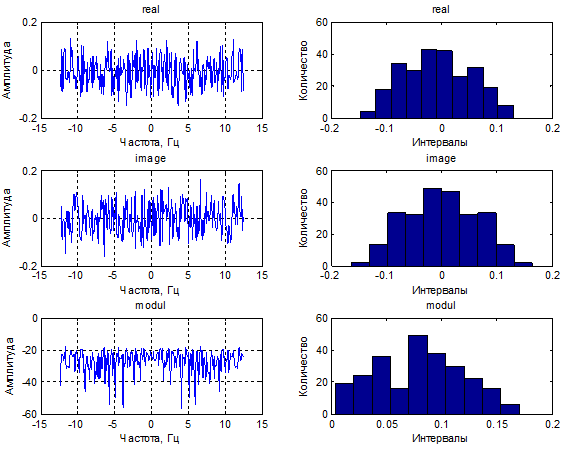
Сравнение СПМ центрированного и нецентрированного шума:
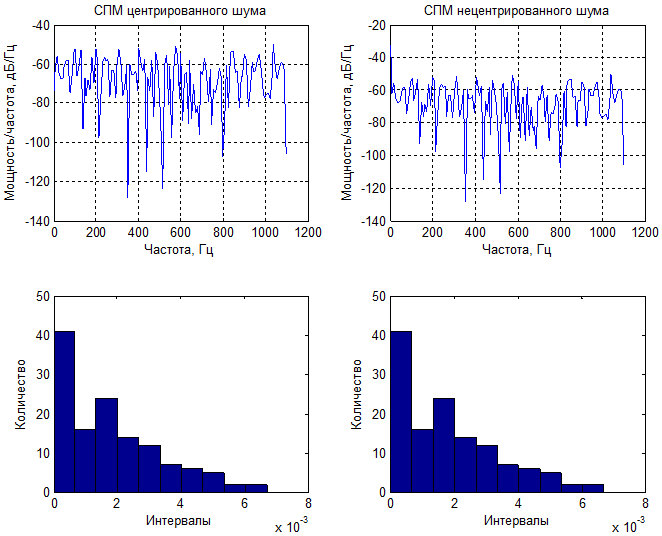
Суммарная мощность нецентрированного процесса ( σ2 + m2) = 1.9108
Mощность нецентрированного процесса по спектральным оценкам = 1.9042
Суммарная мощность центрированного процесса ( σ2 + m2) = 1.7003
Mощность центрированного процесса по спектральным оценкам = 1.6936
3. Смесь гармонического сигнала и шума
3) С/Ш=-40 дБ
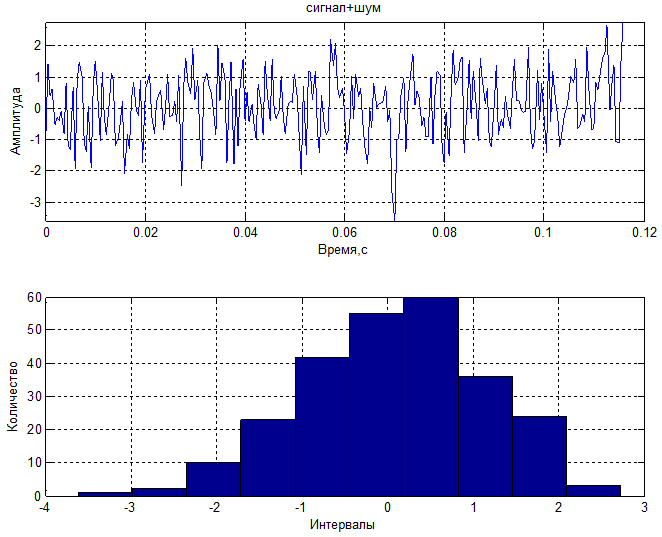
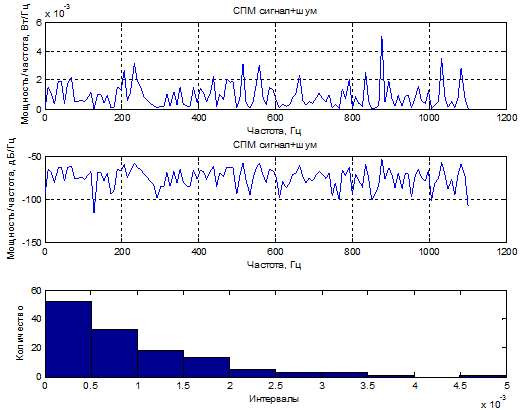
1) С/Ш=-20 дБ
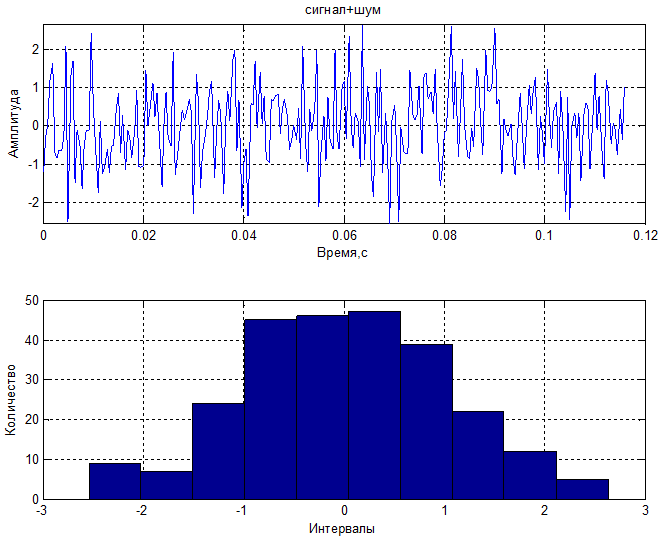
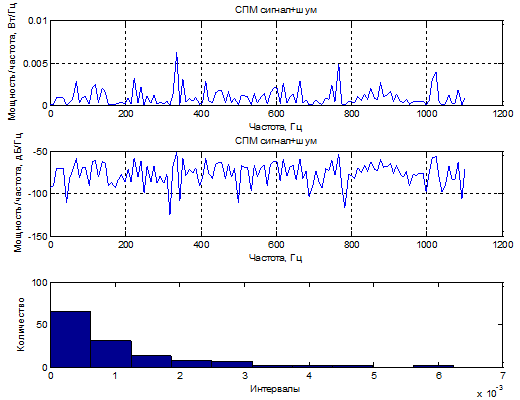
2) С/Ш=0 дБ
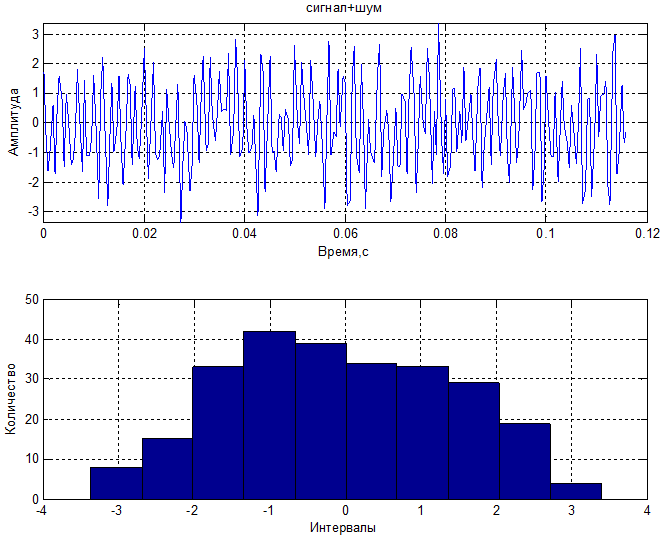
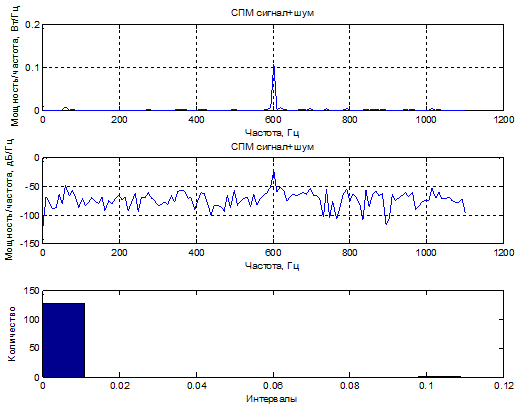
3) С/Ш=20 дБ
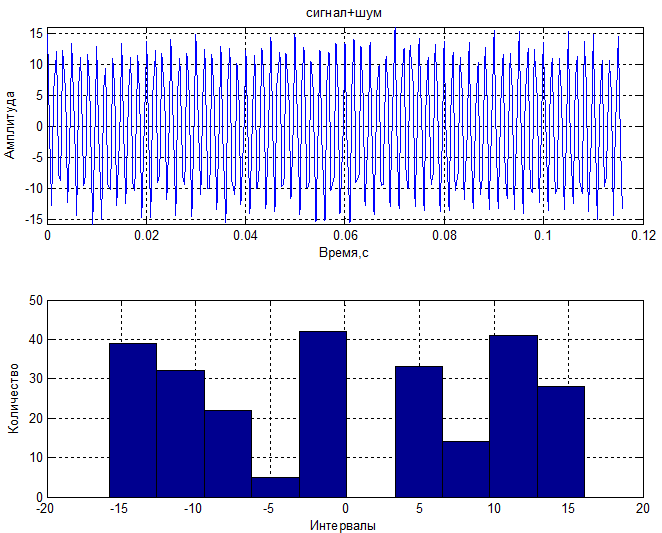
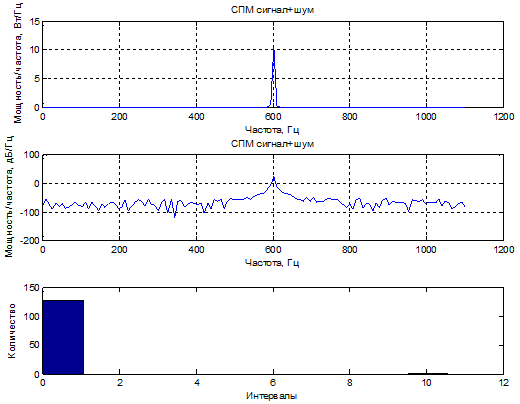
Вывод: При суммировании Гауссова шума его мощность падает в корень из n раз, где n – количество усредняемых кусков. В данном случае можно обнаружить гармонический сигнал при соотношении сигнал/шум 0 дБ и 20 дБ.
Код программы:
Fd=2200; %частота дискретизации
N=1024; %число отсчетов
t=(0:N-1)/Fd;
T=N/Fd; %длина реализации (интервал наблюдения)
df=1/T; %разрешение по частоте
Fs1=600; %основная частота сигнала
Fs2=50; %модулирующая частота
q0=0;
%________________АМПЛИТУДНАЯ МОДУЛЯЦИЯ_____________________
tetaAM=0.5%модулирующий параметр для ам
Us=8*sin(2*pi*Fs1*t+q0);%модулируемый сигнал (несущее колебание)
S=sin(2*pi*Fs2*t);% модулирующий сигнал (информационный сигнал)
Ua=8*sin(2*pi*Fs1*t+q0).*(1+tetaAM*sin(2*pi*Fs2*t));%модулированный сигнал
x1=fft(Ua)/N;
X1=fftshift(x1);
mo=mean(Ua);
disp=cov(Ua);
Pt=mo*mo+disp
figure(1)
subplot(4,1,1);
plot(t,Us);
axis([0,T/4,min(Us)-2,max(Us)+2])
title('модулируемый сигнал');
xlabel('Время,c');
ylabel('Амплитуда');
grid on;
subplot(4,1,2);
plot(t,S);
axis([0,T/4,min(S)-2,max(S)+2])
title('модулирующий сигнал');
xlabel('Время,c');
ylabel('Амплитуда');
grid on;
subplot(4,1,3);
plot(t,Ua);
axis([0,T/4,min(Ua)-2,max(Ua)+2])
title('Амплитудно-модулированный сигнал');
xlabel('Время,c');
ylabel('Амплитуда');
grid on;
subplot(4,1,4);
f=(-N/2:N/2-1)*df;
plot(f,10*log(abs(X1)));
title('FFT амплитудно-модулированного сигнала');
xlabel('Частота, Гц');
ylabel('Мощность/частота, дБ/Гц');
grid on;
%____________________ФАЗОВАЯ МОДУЛЯЦИЯ__________________________
tetaPM=0.5; %индекс фазовой модуляции
Up=8*cos(2*pi*Fs1*t+tetaPM*sin(2*pi*Fs2*t)+q0);
mo=mean(Up);
disp=cov(Up);
Pt=mo*mo+disp
x11=fft(Up)/N;
X11=fftshift(x11);
figure(2)
subplot(2,1,1);
plot(t,Up);
axis([0,T/8,min(Up)-2,max(Up)+2])
title('Фазо-модулированный сигнал');
xlabel('Время,c');
ylabel('Амплитуда');
grid on;
subplot(2,1,2);
f=(-N/2:N/2-1)*df;
plot(f,10*log(abs(X11)));
title('FFT фазо-модулированного сигнала');
xlabel('Частота, Гц');
ylabel('Мощность/частота, дБ/Гц');
grid on;
%__________________ЧАСТОТНАЯ МОДУЛЯЦИЯ_________________________
tetaFM=0.6;%модулирующий параметр для чм
Uf=8*cos(2*pi*(Fs1*t+tetaFM*sin(2*pi*Fs2*t))+q0);
mo=mean(Uf)
disp=cov(Uf)
Pt=mo*mo+disp
x111=fft(Uf)/N;
X111=fftshift(x111);
%мощности сигнала по спектральным характеристикам
dfm=1/T;
mpsd=2* X111.*conj(X111)/dfm;
mspectpower=0.5*sum(mpsd,2)*dfm
figure(3)
subplot(2,1,1);
plot(t,Uf);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.