ЛАБОРАТОРНАЯ РАБОТА № 1
Расчет тонкопроволочных антенн в среде пакета MMANA
Цели работы:
· знакомство с методом интегральных уравнений для тонкопроволочных структур и алгоритмами его реализации;
· знакомство с современными технологиями численного моделирования электродинамических устройств на базе метода интегральных уравнений для тонкопроволочных структур;
· освоение технологии расчета тонкопроволочных антенн в среде пакета MMANA.
Метод интегральных уравнений для тонкопроволочных структур
Тонкопроволочные структуры находят широкое применение в различных приложениях прикладной электродинамики. Они входят в состав широкого класса антенных систем. Сеточные проволочные структуры используются для аппроксимации проводящих поверхностей при достаточной густоте сеток.
Проводник является тонкопроволочным, если его длина много больше длины волн, а толщина много меньше длины волны. В тонкопроволочном приближении считается, что распределение плотности тока на поверхности проводника зависит только от продольной координаты и не зависит от азимутальной координаты.
Рассмотрим основы методики расчета распределения электрического тока на поверхности проводников, основанной на методе интегральных уравнений для тонкопроволочных структур [1,2].
Граничное условие для идеального проводника имеют вид
![]() ,
(1)
,
(1)
где ![]() -
нормаль к поверности идеально проводящего тела.
-
нормаль к поверности идеально проводящего тела.
Интегральное уравнение электрического поля (ИУЭП)
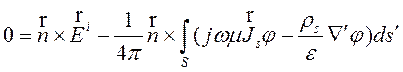 .
(2)
.
(2)
Для простоты запишем уравнение (2) в виде
![]() (3)
(3)
Интегральные уравнения в электродинамических задачах редко имеют аналитическое решение. Одним из наиболее широко используемых на практике численных методов решения интегрального уравнения является метод моментов (МОМ). Рассмотрим применение этого метода для решения операторного уравнения вида
![]() .
(4)
.
(4)
Суть метода моментов состоит в следующем:
1) Для
разложения неизвестной функции используется система базисных функций ![]() из области
определения оператора
из области
определения оператора
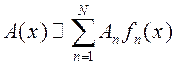 .
(5)
.
(5)
2) Определяется
скалярное произведение тангенциальных векторных функций на поверхности ![]() :
:
![]() .
(6)
.
(6)
3) Определяется
система пробных функций, принадлежащих области значений оператора ![]() :
:
![]() (7)
(7)
4) Берется
скалярное произведение пробных функций с результатом подстановки ряда в
оператор ![]() :
:
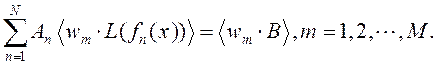 (8)
(8)
Это уравнение
определяет М соотношений для N неизвестных значений ![]() . Здесь
приравниваются пробные проекции операторного уравнения на пространство пробных
функций. Поскольку это линейная система уравнений, то она идеально подходит для
численного решения. Применение этой процедуры к выражению (3), где
. Здесь
приравниваются пробные проекции операторного уравнения на пространство пробных
функций. Поскольку это линейная система уравнений, то она идеально подходит для
численного решения. Применение этой процедуры к выражению (3), где
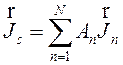 .
(9)
.
(9)
Приводит к соотношению
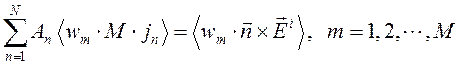 ,
(10)
,
(10)
которое может быть записано в виде
![]() ,
(11)
,
(11)
где
![]() (12)
(12)
Описанный выше алгоритм составляет основу метода моментов (МОМ).
Назначение и возможности пакета MMANA
Пакет MMANA [3] базируется на вычислительном
ядре системы MININEC и
реализует методику решения интегрального уравнения для тонкопроволочных
структур методом моментов. Пакет MMANA
предназначен для расчета электродинамических характеристик антенных
систем, представляющих собой конструкции, состоящие из набора прямолинейных
проводящих отрезков c цилиндрическим
поперечным сечением. Пакет позволяет моделировать сплошные проводящие тела
используя аппроксимацию их поверхности проволочной сеткой. Алгоритм решения предусматривает
разбиение проволочной конструкции на совокупность сегментов, размеры которых не
должны превышать ![]() . В каждый
сегмент может быть внесена комплексная нагрузка. Моделирование возбуждения
сводится к подключению сосредоточенных источников в заданные проволочные
сегменты. Максимальное число источников ограничено количеством проволочных
сегментов. Амплитудно-фазовое распределение системы источников может быть
произвольно.
. В каждый
сегмент может быть внесена комплексная нагрузка. Моделирование возбуждения
сводится к подключению сосредоточенных источников в заданные проволочные
сегменты. Максимальное число источников ограничено количеством проволочных
сегментов. Амплитудно-фазовое распределение системы источников может быть
произвольно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.