Направление
дифрагированных лучей зависит только от
расстояния ![]() , а их интенсивность –
от природы атомов и их расположения в элементарной ячейке. Можно показать, что
амплитуда волны, дифрагированной в направлении hkl,
является структурным фактором
, а их интенсивность –
от природы атомов и их расположения в элементарной ячейке. Можно показать, что
амплитуда волны, дифрагированной в направлении hkl,
является структурным фактором ![]() , описываемым уравнением:
, описываемым уравнением:
![]() =
= ![]()
![]() exp
exp , где
, где ![]() ,
,![]() ,
,![]() – относительные координаты j-го атома в
элементарной ячейке.
– относительные координаты j-го атома в
элементарной ячейке.
В общем случае
структурный фактор представляет собой комплексное число, определяемое модулем ![]() и фазой
и фазой ![]() . Интенсивность дифрагированного
излучения определяется квадратом амплитуды:
. Интенсивность дифрагированного
излучения определяется квадратом амплитуды:
![]()
Легко показать, что если кристаллическая структура имеет центр инверсии, структурный фактор является уже не комплексным, а действительным числом, а фаза jравна 0 или p и
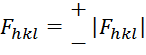
Комплексные соединения
Комплексные соединения составляют наиболее обширный и разнообразный класс неорганических веществ. К ним принадлежат также многие металлорганические соединения, связывающие воедино ранее разобщённые неорганическую химию и органическую химию.
Многие комплексные соединения – витамин В12, гемоглобин, хлорофилл и другие – играют большую роль в физиологических и биохимических процессах. Исследование свойств и пространственного строения комплексных соединений оказалось чрезвычайно плодотворным для кристаллохимии, изучающей зависимость физико-химических свойств веществ от структуры образуемых ими кристаллов, и породило новые представления о природе химической связи. К ценным результатам привело применение комплексных соединений и в аналитической химии. Не будет преувеличением сказать, что успехи теоритической и прикладной химии за последние годы во многом связаны именно с изучением комплексных соединений.
 Наиболее удачно свойства и строение комплексных
соединений объясняет координационная теория, предложенная в 1893 г. А. Вернером.·
Наиболее удачно свойства и строение комплексных
соединений объясняет координационная теория, предложенная в 1893 г. А. Вернером.·
![]() Альфред Вернер – швейцарский химик, лауреат Нобелевской премии, один из создателей учения о комплексных соединениях. Научная деятельность Вернера протекала в Цюрихском
университете, профессором которого он был с 1893 г. Вернер синтезировал большое
число новых комплексных соединений, систематизировал
ранее известные и вновь полученные комплексные соединения и разработал экспериментальные
методе доказательства из
строения.
Альфред Вернер – швейцарский химик, лауреат Нобелевской премии, один из создателей учения о комплексных соединениях. Научная деятельность Вернера протекала в Цюрихском
университете, профессором которого он был с 1893 г. Вернер синтезировал большое
число новых комплексных соединений, систематизировал
ранее известные и вновь полученные комплексные соединения и разработал экспериментальные
методе доказательства из
строения.
Лиганды
Лиганды, занимающие во внутренней координационной сфере одно место, называются монодектатными. Существуют лиганды, занимающие во внутренней сфере два или несколько мест. Такие лиганды называются би- и полидентатными.
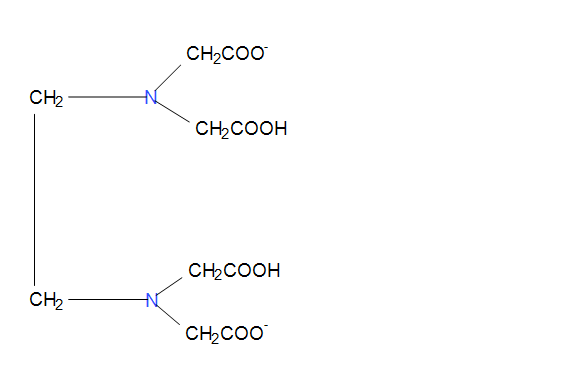
Примерами бидентатных лигандов могут служить оксалатный ион С2О4 2- и молекула этилендиамина (NH2CH2CH2NH2). Четырёхде6нтатиым лигандом является двухзарядный анион этилендиаминтетрауксусной кислоты.
Выбор Катализаторов
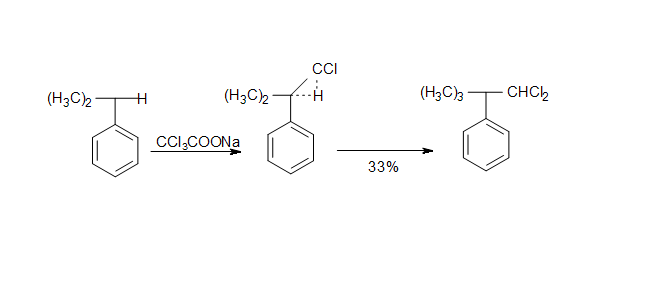
Положение равновесия зависит от природу реагентов и от растворителя: высокая диэлектрическая проницаемость сдвигает равновесие в сторону образования карбениевого иона. Затем электрофильный агент реагирует с ароматической молекулой:
 Выбор катализатора определяется реакционной способностью
ароматического
соединения. Чаще всего применяют хлорид алюминия и только для
очень реакционноспособных систем (например,
для тиофена) используются хлорид цинки, серную кислоту и др.
Выбор катализатора определяется реакционной способностью
ароматического
соединения. Чаще всего применяют хлорид алюминия и только для
очень реакционноспособных систем (например,
для тиофена) используются хлорид цинки, серную кислоту и др.
ФОРМУЛЫ
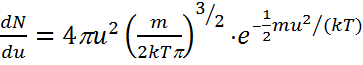 , где
, где
· u – скорость;
· k – константа Больцмана;
· T – температура, К;
· M – масса молекулы;
· dN/du – плотность распределения частиц;
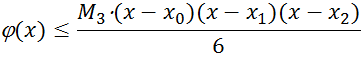
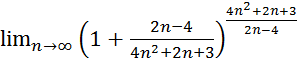 =e
=e
ДИАГРАММЫ
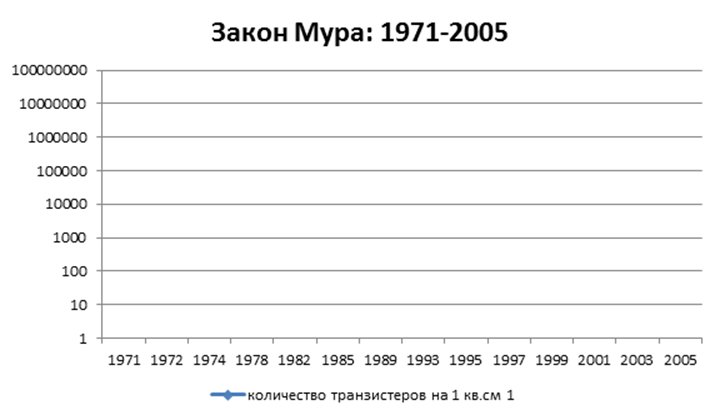
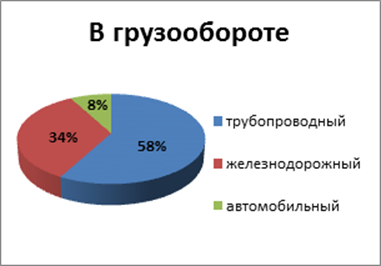
Доля видов транспорта
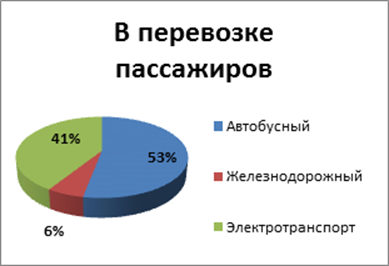
ГРАФИКИ
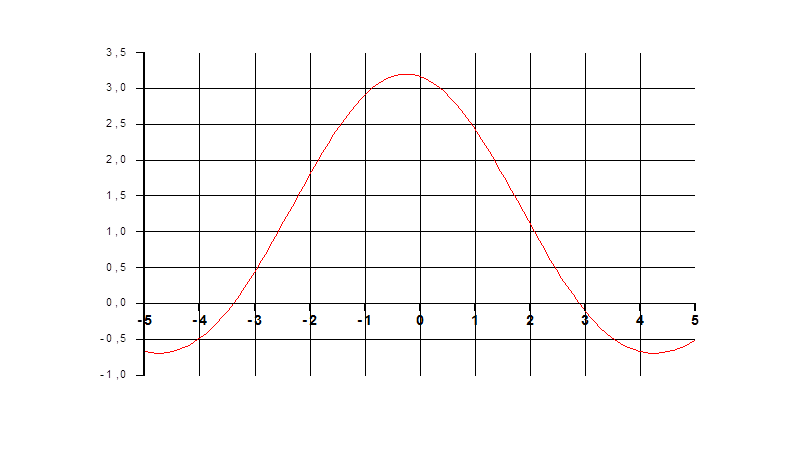
График функции ![]() на отрезке
на отрезке ![]()
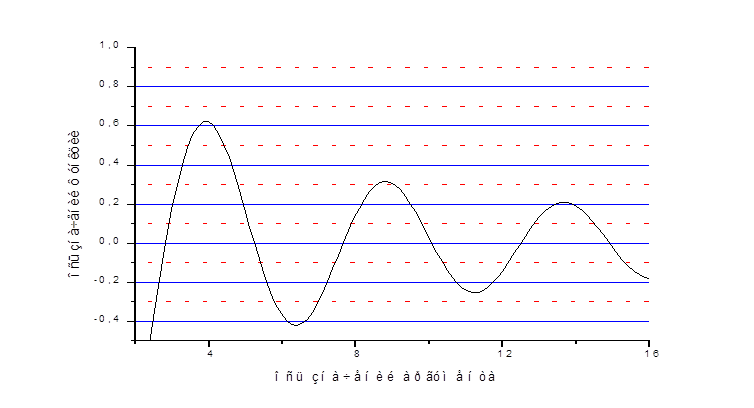
График функции 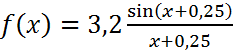
ПРИЛОЖЕНИЕ
Исходные данные диаграммы №1
1971 2 300
1972 3 500
1974 6 000
1978 29 000
1982 134 000
1985 275 000
1989 1 200 000
1993 3 100 000
1995 5 500 000
1997 7 500 000
1999 1 9000 000
2001 4 4000 000
2009 9 5200 000
2005 190 000 000
Оптически активные соли
|
СОЛИ |
Tпл С |
Растворимость в воде при 21 С |
|
|
|
(+) - миндальнокислый |
80 |
1.08 |
+152.4 |
|
|
(+) - Цинхонин |
||||
|
(–) - миндальнокислый |
165 |
2.05 |
+92.1 |
|
|
(+) - виннокислый |
198 |
– |
-12.6 |
|
|
(–) - Ментиламин |
||||
|
(–) - виннокислый |
194 |
– |
-42.0 |
|
|
(–) – Ментиламин |
мезовиннокислый |
218 |
– |
-32.1 |
ЛИТЕРАТУРА
Основная
1. Глинка, Н.Л. Общая Химия: Учебное пособие для вузов / Н. Л. Глинка. – Л.: Химия. 1983.
2. Бутырская, Е. В. Компьютерная химия: основы теории и работа с программами Gaussian и Gauss View / Е. В. Бутырская. – М.: Солон-пресс, 2011.
3. Гмурман, В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман. – М.: Высшая школа, 2001.
4. Орлов, А. И. Прикладная статистика. Учебник / А. И. Орлов. – М.: Экзамен, 2004.
5. Чистяков, В. П. Курс теории вероятностей / В. П. Чистяков. – М.: Наука, 1978
Дополнительная
6. Колемаем, В. А. Теория вероятностей и математическая статистика / В. А. Колемаев, В. Н. Калинина. – М.:Инфра-М, 2001.
7. Hays, W. L. Statistics / W. L. Hays. – London, Holt, Rinehart and Winston, 1981,
СОДЕРЖАНИЕ
1. Аннотация ................................................................................................. 3
2. Структурные факторы и функция распределения электронной плотности 4
3. Комплексные соединения ........................................................................ 5
4. Лиганды .................................................................................................... 6
5. Формулы ................................................................................................... 7
6. Диаграммы ................................................................................................ 8
7. Графики .................................................................................................... 9
8. Приложение ............................................................................................ 10
9. Литература ............................................................................... 11
[1]Из данного уравнения очевидно, что волна, дифрагированная в направлении hkl, является суммой волн, рассеянных отдельными атомами ячейки
· Для объяснения строения и свойств комплексных соединений Вернер выдвинул идею о координации, т.е. о пространственном окружении иона металла анионами или нейтральными молекулами. Координационная теория легла в основу современных представлений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.