Лабораторная работа №1
Исследование детерминированных процессов
Выполнила студентка
5 курса 5 группы
Минск, 2012
1) Гармонический процесс (A0 = 1 В; P0 = 0.2 В; phi = 0.3; fd=880 Гц; N=256; df =3.4375 Гц; dt=0.0011 с ; T= 0.2898 с) частота основного тона кратна разрешению по частоте ( fs= df*25=85.9375 Гц)
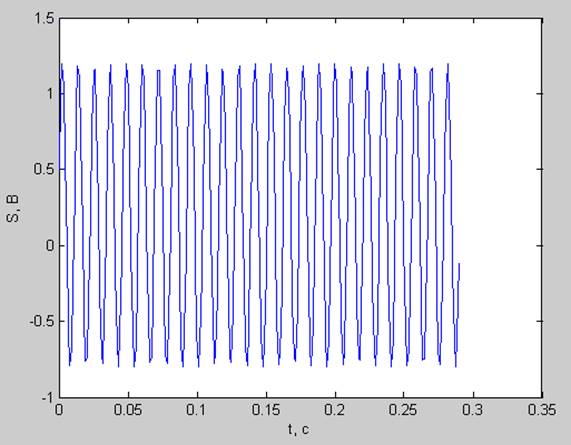
pt =0.5400
ps =0.5400
m =0.2000
disper =0.5020
p =0.5420
Спектр мощности:
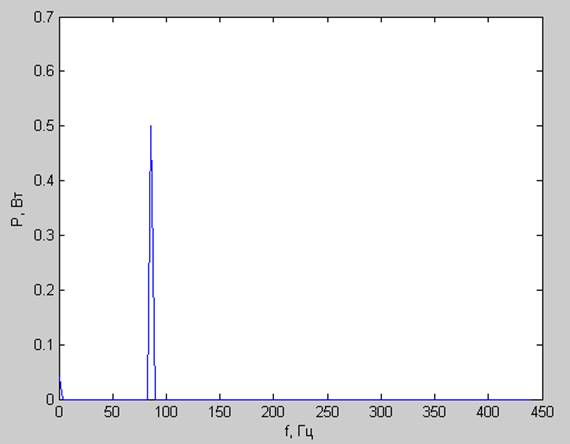
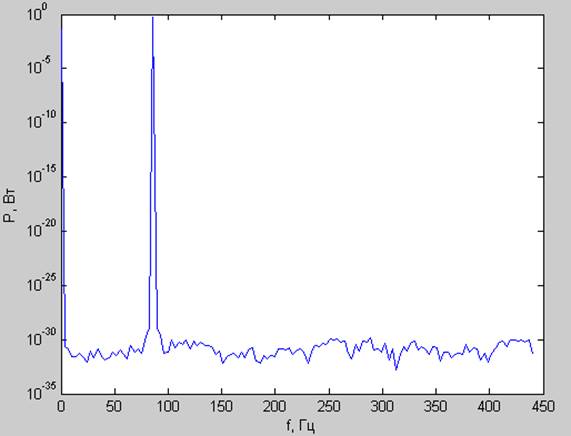
Корреляционная функция:
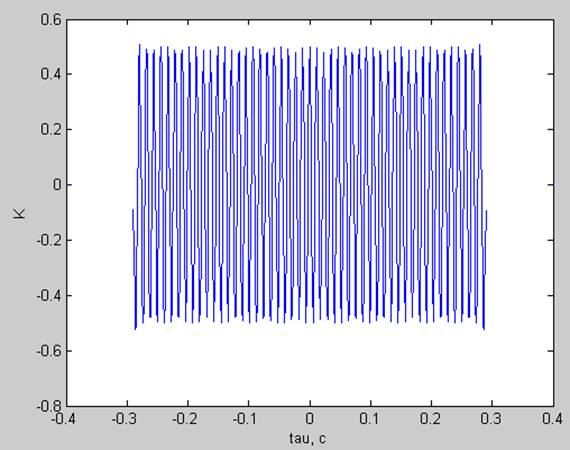
частота основного тона не кратна разрешению по частоте ( fs= df*24.5= 84.2188 Гц)
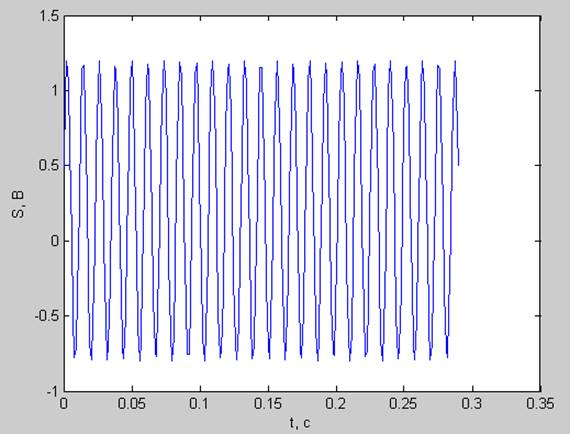
pt =0.5453
ps =0.5453
m =0.2132
disper =0.5018
p =0.5472
2) Периодические процессы («меандр», «равнобокую» и «кособокую» пила – |_|ˉˉ|_|ˉˉ|_|ˉˉ|_|ˉˉ|_ /|/|/|/|/|/| |\|\|\|\|\|\ /\/\/\/\/\/\/.)
Меандр (A0 = 1 В; P0 = 0.2 В; phi = 0.3; fd=880 Гц; N=256; df =3.4375 Гц; dt=0.0011с ; T= 0.2898 с)
частота основного тона кратна разрешению по частоте ( fs= df*25=85.9375 Гц)
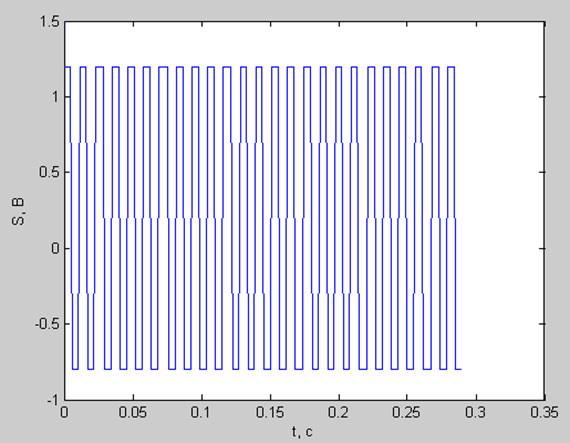
pt =1.0400
ps =1.0400
m =0.2000
disper =1.0039
p =1.0439
Спектр мощности:
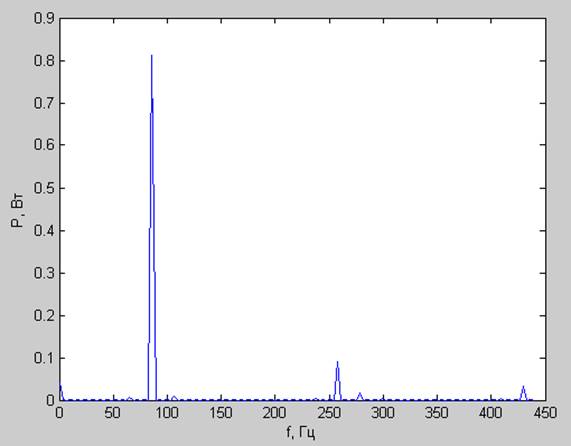
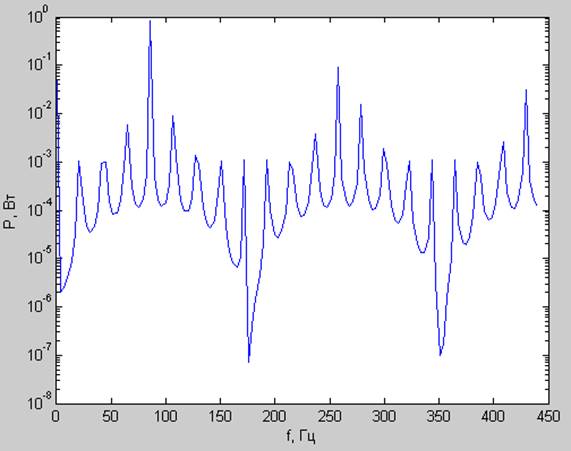
Корреляционная функция:
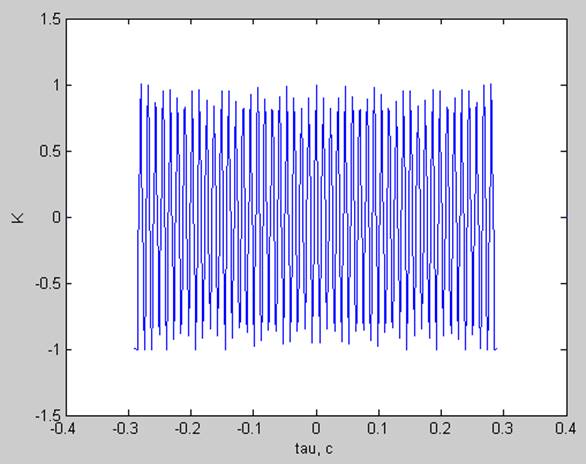
частота основного тона не кратна разрешению по частоте ( fs= df*24.5= 84.2188 Гц)
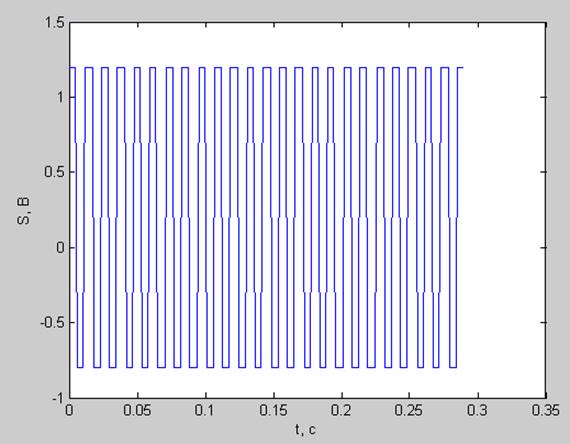
pt =1.0525
ps =1.0525
m =0.2313
disper =1.0029
p =1.0564
Равнобокая пила (A0 = 1 В; P0 = 0.2 В; phi = 0.3; fd=880 Гц; N=256; df =3.4375 Гц; dt=0.0011 с; T= 0.2898 с)
частота основного тона кратна разрешению по частоте ( fs= df*25= 85.9375 Гц)
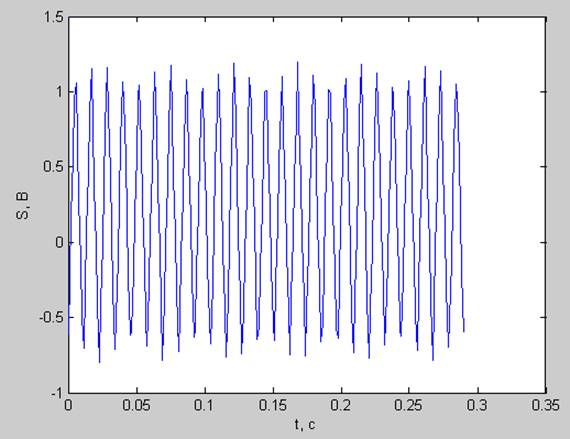
pt =0.3733
ps =0.3733
m =0.2000
disper =0.3346
p =0.3746
Спектр мощности:
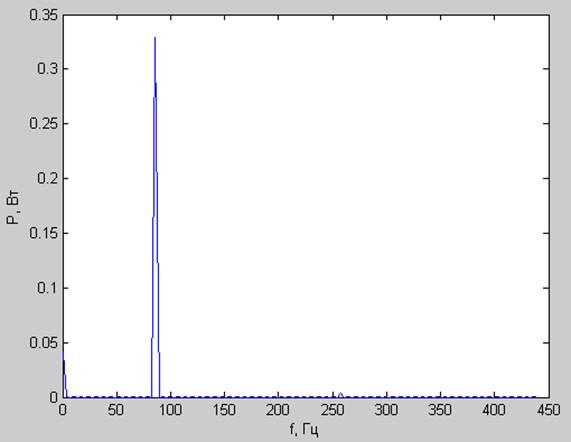
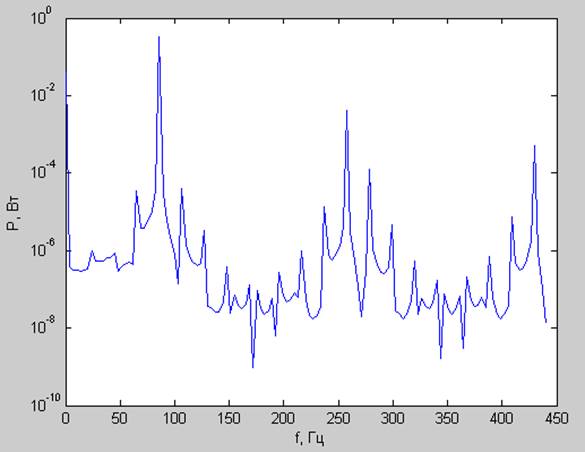
Корреляционная функция:
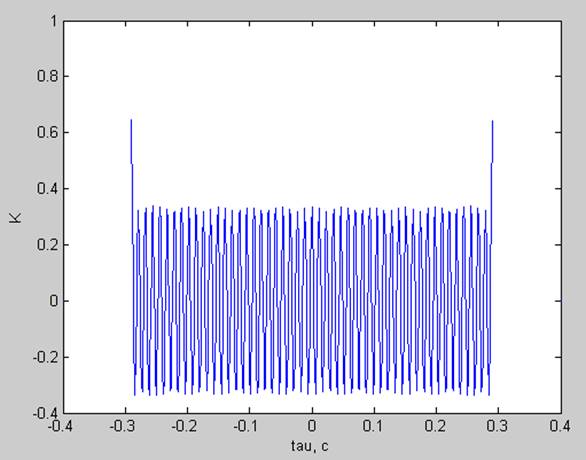
частота основного тона не кратна разрешению по частоте ( fs= df*24.5= 84.2188 Гц )
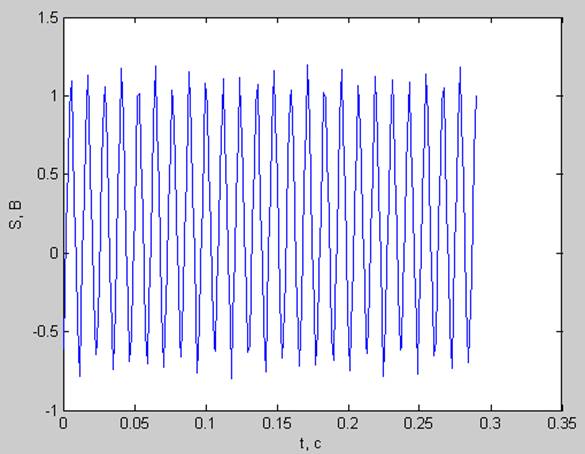
pt =0.3733
ps =0.3734
m =0.2000
disper =0.3346
p =0.3746
Кособокая пила ( |\|\|\|\|\|\) (A0 = 1 В; P0 = 0.2 В; phi = 0.3; fd=880 Гц; N=256; df =3.4375 Гц; dt=0.0011 с; T= 0.2898 с)
частота основного тона кратна разрешению по частоте ( fs= df*25= 85.9375 Гц)
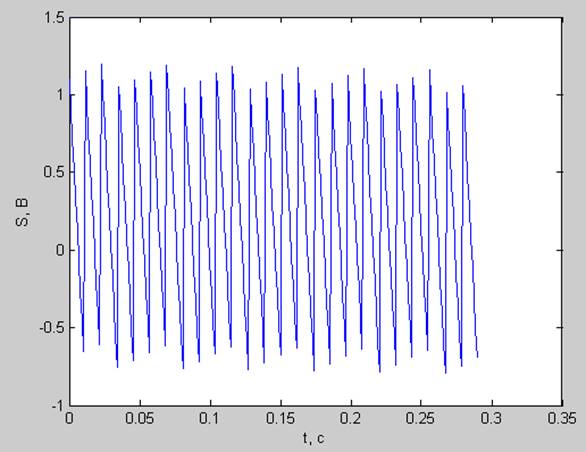
pt =0.3742
ps =0.3742
m =0.2022
disper =0.3346
p =0.3755
частота основного тона не кратна разрешению по частоте ( fs= df*24.5= 84.2188 Гц)
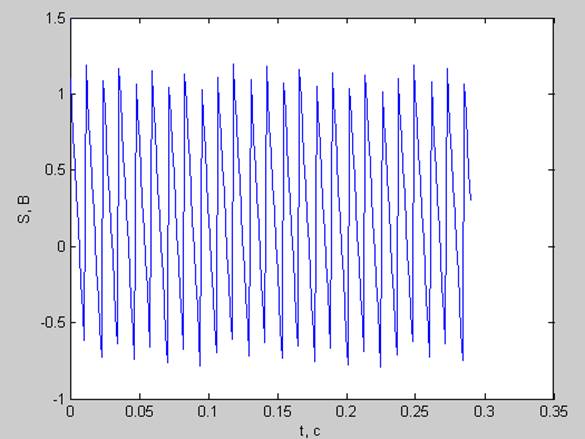
pt =0.3797
ps =0.3797
m =0.2158
disper =0.3344
p =0.3810
Кособокая пила (/|/|/|/|/|/|) (A0 = 1 В; P0 = 0.2 В; phi = 0.3; fd=880 Гц; N=256; df =3.4375 Гц; dt=0.0011 с; T= 0.2898 с)
частота основного тона кратна разрешению по частоте ( fs= df*25= 85.9375 Гц )
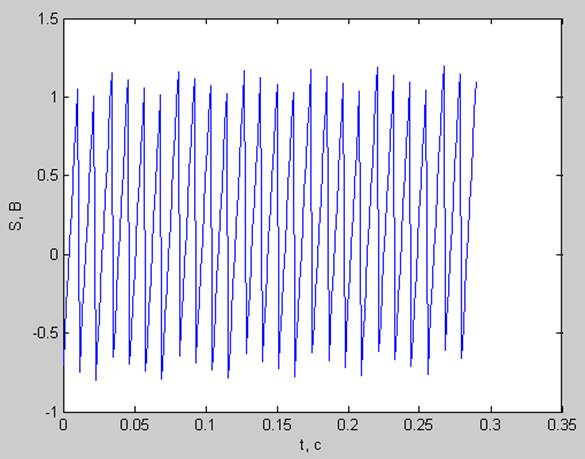
pt =0.3725
ps =0.3725
m =0.1978
disper =0.3346
p =0.3738
Спектр мощности:
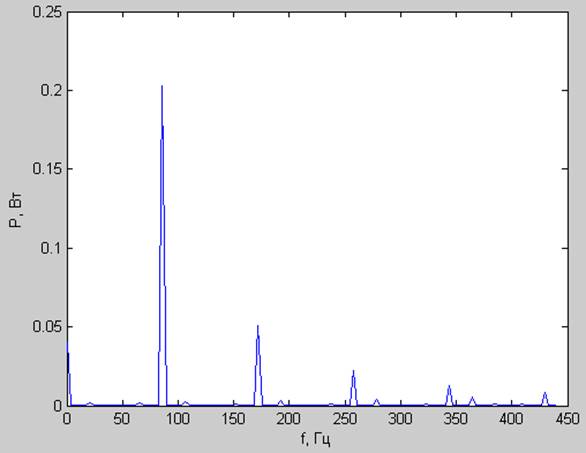
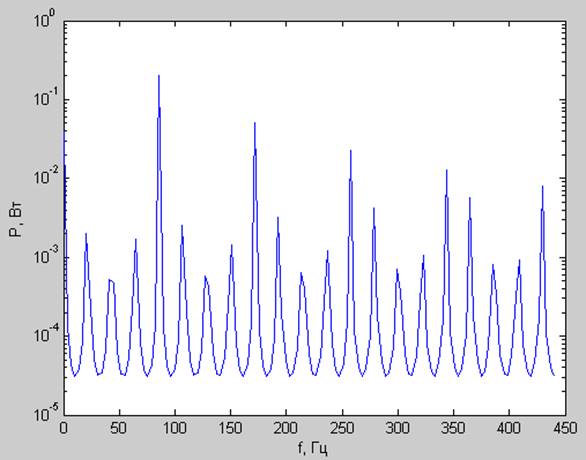
Корреляционная функция:
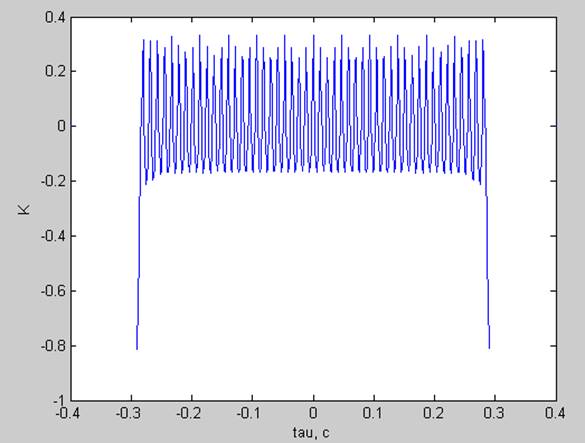
частота основного тона не кратна разрешению по частоте ( fs= df*24.5= 84.2188 Гц )
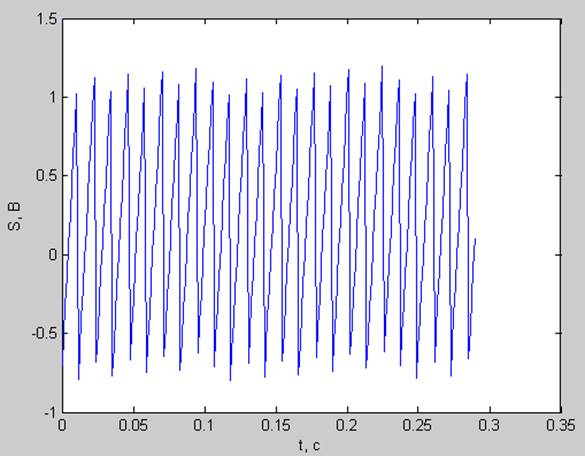
pt =0.3670
ps =0.3670
m =0.1842
disper =0.3344
p =0.3683
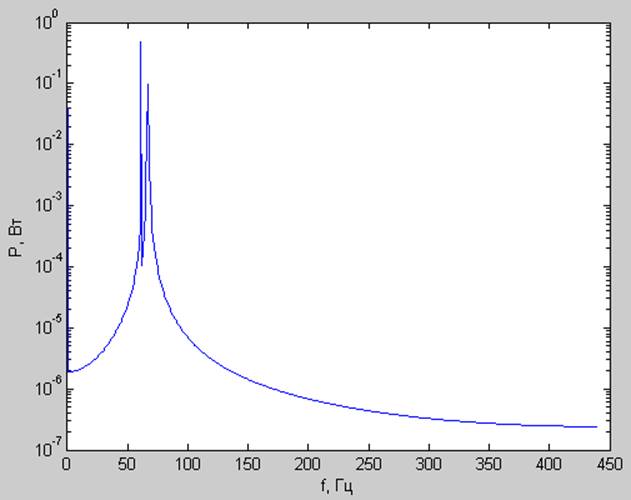
3) Квазипериодический процесс (A1 = 1 В; A2 = 0.5 В; P0=0.2 В; f1 = 61 Гц; f2 = 66.8 Гц; fd=880 Гц; N=1024; df = 0.8594 Гц; dt= 0.0011с ; T= 1.1625 с)
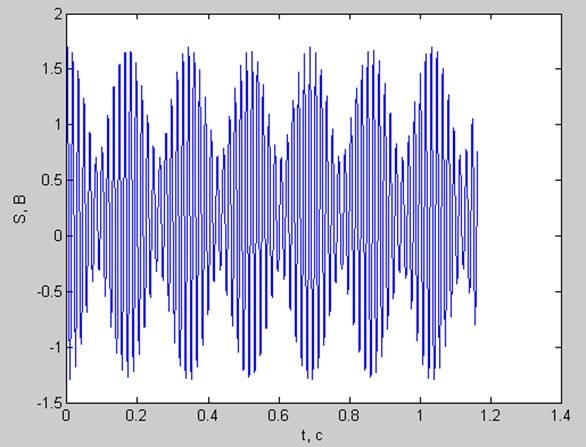
pt =0.6529
ps =0.6529
m =0.1990
disper =0.6139
p =0.6535
Спектр мощности:
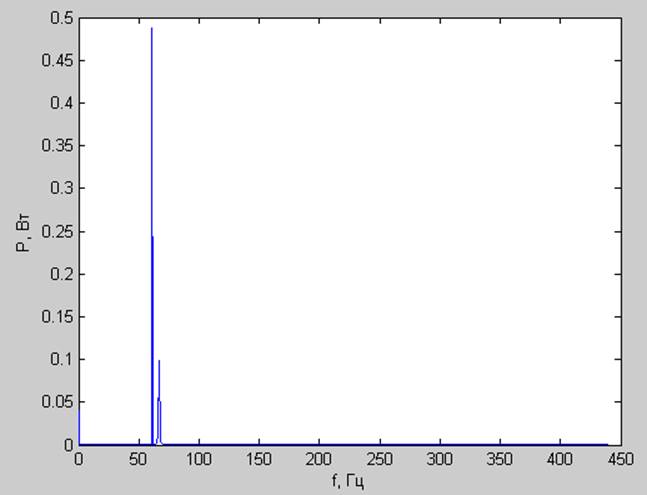
Корреляционная функция:
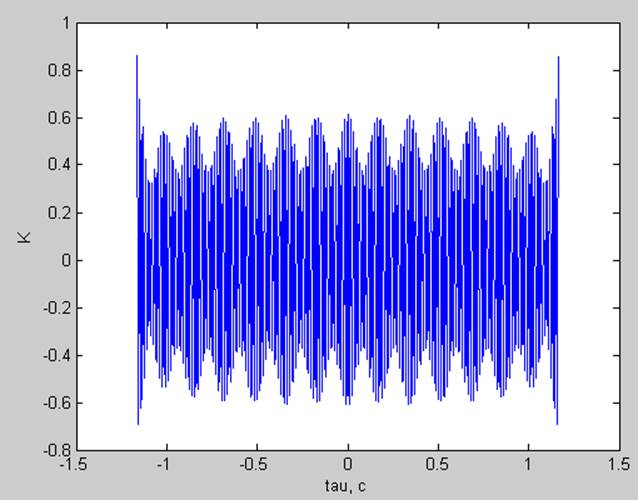
4) Непериодический процесс ( fd=880 Гц; N=256; df =3.4375 Гц; dt =0.0011 с; T=0.2898 c)
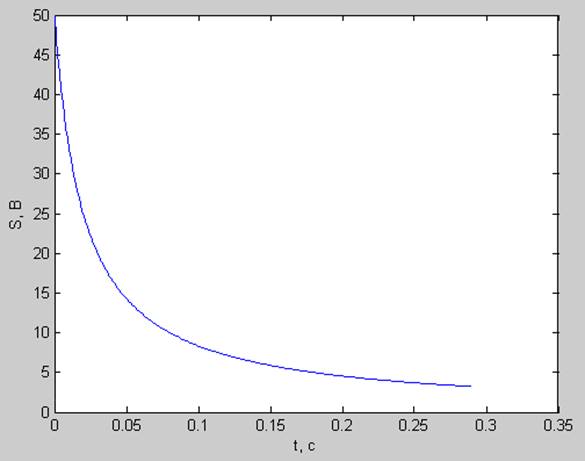
pt =165.7737
ps =256.4891
m =9.5240
disper =75.3615
p =166.0681
Спектр мощности:
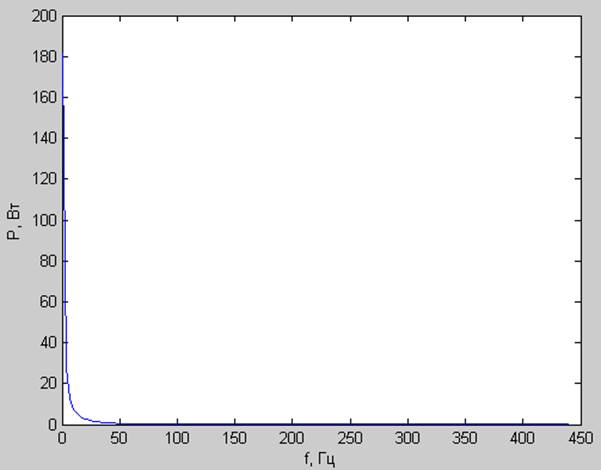
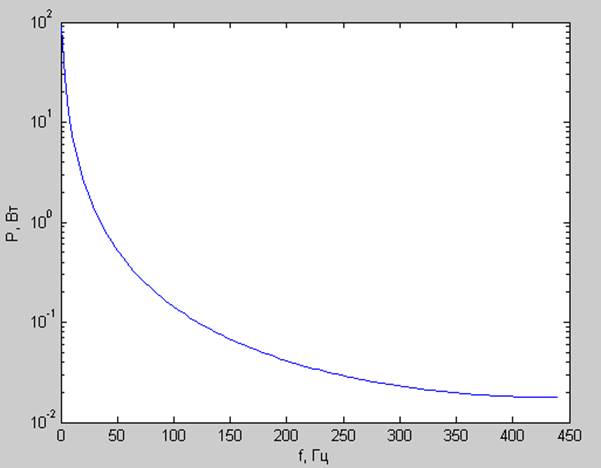
Корреляционная функция:
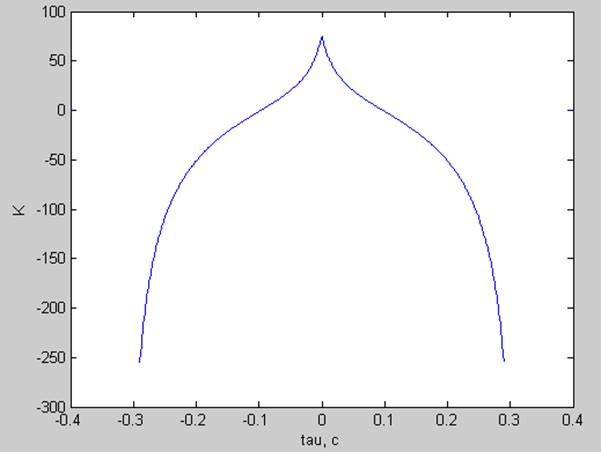
Выводы: В спектре гармонического сигнала наблюдала один пик, соответствующий частоте сигнала и постоянную составляющую сигнала. В случае меандра в спектре видно нечетные гармоники и постоянную составляющую сигнала. В случае пилы в спектре видно четные и нечетные гармоники и постоянную составляющую сигнала. В случае квазипериодического процесса, образованного сложением двух гармонических близких по частоте сигналов в спектре видно два пика, соответствующих этим частотам. Различие в величине пиков обусловлено различием амплитуд исходных сигналов.
Код программы:
clear all
clc
format compact
fd=880;
dt=1/fd
N=256;
df=fd/N
fs=df*25
N2 =N/2;
N21 =N2+1;
Tr=(N-1)*dt
t = 0:dt:Tr;
A0 = 1;
P0 = 0.2;
phi = 0.3;
y =A0*sin(2*pi*fs*t+phi)+P0;
% y=A0*square(2*pi*fs*t+phi)+P0;
% y=A0*sawtooth(2*pi*fs*t+phi,0.5)+P0;
% y=A0*sawtooth(2*pi*fs*t+phi,0)+P0;
% y=A0*sawtooth(2*pi*fs*t+phi,1)+P0;
% f1 = 61;
% f2 = 66.8;
% a1 = 1;
% a2 = 0.5;
% y = a1*cos(2*pi*f1*t) + a2*cos(2*pi*f2*t)+P0;
%y = 1./(t+0.02);
pt=sum(y.^2)/N
figure(1)
plot(t,y)
%====
hold on
plot(0,1.5);
%====
Xlabel('t, с')
Ylabel('S, В')
Sk=fft(y,N)/N;
ff=(0:N2)*df;
Sm=(real(Sk(1:N21)).^2+imag(Sk(1:N21)).^2)*2;
Sm(1)=Sm(1)/2;
figure(2)
plot(ff,Sm)
Xlabel('f, Гц')
Ylabel('P, Вт')
ps=sum(Sm)
figure(3)
semilogy(ff,Sm)
Xlabel('f, Гц')
Ylabel('P, Вт')
m=mean(y)
disper=cov(y)
p=(mean(y))^2+(cov(y))
[K, tt]=xcorr(y-m,'unbiased');
figure(4)
plot(tt*dt,K)
Xlabel('tau, с')
Ylabel('K')
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.