Исследование колебаний системы с одной степенью свободы. Система с одной степенью свободы, движение груза по балке. Собственные частоты и формы колебаний, страница 4

Номер	Масса m(тонны)	Коэффициент вязкости в	Полупролет а, м	Стрела подъема f, м	Жесткость ЕА, кН
1	1	0	2	7	1000
2	2	1	3	6	2000
3	3	2	4	5	3000
4	4	3	5	4	4000
5	5	0	6	3	1000
6	1	1	2	2	2000
7	2	2	3	7	3000
8	3	3	4	6	4000
9	4	0	5	5	1000
10	5	1	6	4	2000
11	1	2	2	3	3000
12	2	3	3	2	4000
13	3	0	4	7	1000
14	4	1	5	6	2000
15	5	2	6	5	3000
16	1	3	2	4	4000
17	2	0	3	3	1000
18	3	1	4	2	2000
19	4	2	5	7	3000
20	5	3	6	6	4000
21	1	0	2	5	1000
22	2	1	3	4	2000
23	3	2	4	3	3000
24	4	3	5	2	4000
25	5	0	6	7	1000
26	1	1	2	6	2000
27	2	2	3	5	3000
28	3	3	4	4	4000
29	4	0	5	3	1000

	2
			3

1

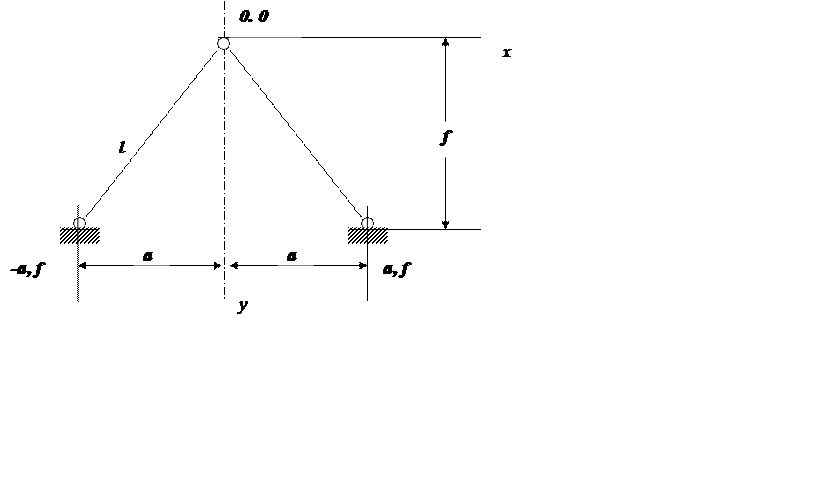
Рис.1.

ВВОД ИСХОДНЫХ ДАННЫХ.

End – нажимать, если менять данные нет необходимости,

Esc – нажимать, если требуется изменить исходные данные

(изменение данных – набрать необходимое число на клавиатуре в формате англ. языка),

Enter – нажимать после каждого введенного данного.

 Вводятся: масса m в тоннах,

коэффициент вязкости в,

в табличной форме координаты фермы (рис.1)

Номер узла	Координаты узла
	х	у
1	0	0
2	-а	f
3	a	f

в табличной форме длины и жесткости каждого стержня

(длину стержня   сосчитать предварительно).

l	EF
l1	EF1
l2	EF2

Далее вводятся координаты возможного смещения центрального узла

( кинематическое возмущение).

Начальное ускорение принять равным нулю .

Тип внешнего воздействия в этой части работы – тип 0 (свободные колебания).

а) Исследование устойчивости состояния равновесия .

Следует проанализировать по очереди пять положений системы:

1.      х₀ = 0;   у₀ = 0

2.      х₀ = 0;   у₀ = f

2.  х₀ = 0;   у₀ = 2f

3.  х₀ = l₀ ;    у₀ = f

4.  х₀ = -l₀;    у₀ = f

Необходимо выяснить какие из предложенных положений системы соответствуют устойчивому состоянию равновесия, какие – неустойчивому. Для этого в каждом из вариантов координату у₀ следует изменить, задав

у₀ = у₀ +0.1.

В отчете для каждого варианта вычертить схему начального положения системы, зарисовать фазовые диаграммы для каждого из вариантов  и на основании этих данных сделать выводы, какие из состояний устойчивы, какие - неустойчивы.

б) Исследование зависимости "частоты " свободных колебаний от "амплитуды".

Предварительно определяется частота системы в случае малых линейных колебаний: 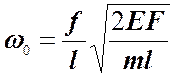. Пояснить получение этой зависимости.

Выбирается начальное положение системы и затем меняется

положение центрального узла, например,:

1.  х₀ = 0;   у₀ = 0.1 f

2.  х₀ = 0;   у₀ = 0.2 f

3.  х₀ = 0;   у₀ = 0.4 f

4.  х₀ =0₀ ;   у₀ = 0.5 f

5.  х₀ = 0;   у₀ = 0.7 f

6.  х₀ = 0;   у₀ = 0.9 f

7.  х₀ = 0;   у₀ = 1 f

8.  х₀ =0 ;    у₀ =-0.5 f

Для каждого варианта с монитора выписываются значения "амплитуды", "частоты" и "периода колебаний".

Результаты можно свести в таблицу:

Начальное у0	"Амплитуда" А, м	"Период" Т, сек.	"Частота" ω 1/сек
0.1 f
0.2 f
0.4 f
0.5 f
0.7 f
0.9 f
1 f
-0.5 f

По этим данным следует построить "скелетную" кривую - зависимость амплитуды от частоты и полученное решение сравнить с частотой при малых перемещениях.

Эту часть можно усложнить:

1.  Изменить жесткость системы, увеличив ее, например, в 100 раз.

2.  Можно исследовать колебания, задав х₀ ≠0.