Исследование колебаний системы с одной степенью свободы. Система с одной степенью свободы, движение груза по балке. Собственные частоты и формы колебаний, страница 3

Потом Enter (если не получилась заданная схема балки то, что необходимо, нажать Esc), затем Enter,…, Enter( пропуская ввод остальных исходных данных – жесткости упругого основания, нагрузки и массы).

INPUT DATA IS OVER (ввод закончен), Enter

ANALYSIS Enter

Вверху в строке справа ввести номер собственной формы колебаний (начать с первой формы) Enter

Затем в той же строке ввести начальное значение первой собственной частоты  - лучше всего – 0. Enter.

Затем в той же строке ввести конечное значение первой собственной частоты  - например – 1. Enter.

Enter, Enter, Enter…идет итерационный поиск до тех,  пор пока наверху не появится строка "введите 0 (процесс поиска закончен) или EPS (другая точность вычислений)". Enter, Enter (погаснет экран), Enter.

Появляется заданная форма колебаний. Срисовать. Списать таблицу отклонения узлов от горизонтали – UY и записать частоту колебаний балки по этой форме SW. Enter.

Все повторяется при поиске следующей формы колебаний. При вводе номера формы – 0 – выход – Ctrl end.

Проверить ортогональность 1-ой и 2-ой  (1-ой и 3-ей)форм колебаний:

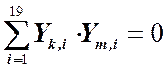 - условие ортогональности k  и m собственных форм.

ВЫВОДЫ.

Определение собственных форм и частот. Условие ортогональности.

.

Лабораторная работа № 4.

КИНЕМАТИЧЕСКОЕ ВОЗМУЩЕНИЕ, СЕЙСМИКА.

Исходные данные:

Номер по журналу	Длина стержня, м	Масса системы m  , т	Жесткость cистемы c ,  кН / м	Вязкость в, кН /м	Коэфф. сейсмич ности kc	Начальные координаты и скорости
1	2	51	1100	0.5	0.2	0
2	3	52	1200	0.6	0.4	0
3	4	53	1300	0.7	0.6	0
4	5	54	1400	0.8	0.8	0
5	6	55	1500	0.9	0.2	0
6	7	56	1600	1.0	0.4	0
7	8	57	1700	1.1	0.6	0
8	9	58	1800	1.2	0.8	0
9	10	59	1900	1.3	0.2	0
10	2	60	2000	1.4	0.4	0
11	3	61	2100	1.5	0.6	0
12	4	62	2200	1.6	0.8	0
13	5	63	2300	1.7	0.2	0
14	6	64	2400	1.8	0.4	0
15	7	65	2500	1.9	0.6	0
16	8	66	2600	2.0	0.8	0
17	9	67	2700	0.5	0.2	0
18	10	68	2800	0.6	0.4	0
19	2	69	2900	0.7	0.6	0
20	3	70	3000	0.8	0.8	0
21	4	71	3100	0.9	0.2	0
22	5	72	3200	1.0	0.4	0
23	6	73	3300	1.1	0.6	0
24	7	74	3400	1.2	0.8	0
25	8	75	3500	1.3	0.2	0
26	9	76	3600	1.4	0.4	0
27	10	77	3700	1.5	0.6	0
28	2	78	3800	1.6	0.8	0
29	3	79	3900	1.7	0.2	0
30	4	80	4000	1.8	0.4	0

После ввода исходных данных перейти к расчету, посмотреть различие между колебанием основания (землетрясение) и колебанием массы, а также определить коэффициент динамики β, нажав кнопку "числа".

1.  Меняя в исходных данных у- значение максимального смещения основания , найти такое значение у_max, при котором наступит резонанс (периоды колебаний массы и основания практически должны совпадать –точность 0.01).

2.  При двух значениях вязкости стержня В= 0 и В = заданному значению построить два графика зависимости между коэффициентом динамики β и периодом колебаний Т₂ (величиной начального смещения - у_max )

ВЫВОД

Сравнить графики с приведенным в СНиП II- 7 81* "Строительство в сейсмических районах" .

Лабораторная работа №5: НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ И

УСТОЙЧИВОСТЬ СОСТОЯНИЙ ФЕРМЫ МИЗЕСА.

ЧАСТЬ 1. Исследование свободных колебаний фермы

Исходные данные: