



I семестр ЛЕКЦИЯ 8
2.5.3 Свободные колебания . Решение уравнения в обратной форме.
![]() Подстановка решения
Подстановка решения ![]() в уравнение в обратной форме
приводит уравнение к виду
в уравнение в обратной форме
приводит уравнение к виду
![]() .
.
Так как уравнение должно выполняться при любом значении t, т.е. в любой момент времени, этой записи эквивалентно алгебраическое матричное однородное уравнение
![]() .
.
Однородная система алгебраических уравнений имеет два варианта решения:
Последнее выражение называется характеристическим уравнением задачи (или частотным, или вековым) и является уравнением n степени относительно величины, обратной ω2
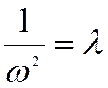 .
.
Например: для системы, имеющей две степени свободы
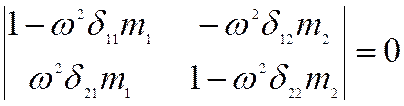
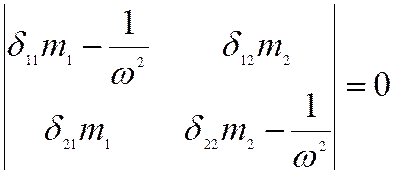
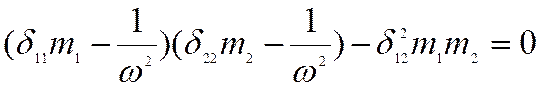
Доказывается, что если исходное положение есть положение устойчивого равновесия, то n корней характеристического уравнения λk (i=1,…, n) являются действительными и положительными числами. λk называются собственными числами или собственными значениями матрицы
![]() .
.
Упорядоченная в порядке убывания и пронумерованная совокупность положительных значений λk образует так называемый спектр собственных чисел
![]() .
.
Каждому собственному числу соответствует свой вектор амплитуд обобщенных координат, удовлетворяющий уравнению
![]() . ( * )
. ( * )
Например, для системы, имеющей две степени свободы
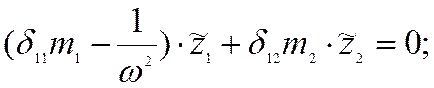
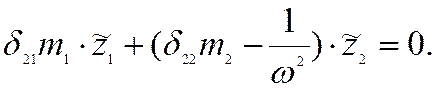
Уравнение ( * ) содержитn неизвестных перемещений
(обобщенных координат, компонент вектора ![]() )
. Однако, в силу (определитель нами приравнен нулю) матрица
коэффициентов однородной системы уравнений является вырожденной, уравнения
линейно зависимы, число независимых уравнений в системе меньше n. Если характеристическое
уравнение имеет «простые» корни (т.е. в спектре нет одинаковых корней), то
число независимых уравнений равно n-1, и компоненты вектора амплитуд
определятся с точностью до множителя. Найденной таким образом – с точностью до
множителя - распределение амплитуд при собственном колебании с частотой ωk называется
собственной формой колебаний.
)
. Однако, в силу (определитель нами приравнен нулю) матрица
коэффициентов однородной системы уравнений является вырожденной, уравнения
линейно зависимы, число независимых уравнений в системе меньше n. Если характеристическое
уравнение имеет «простые» корни (т.е. в спектре нет одинаковых корней), то
число независимых уравнений равно n-1, и компоненты вектора амплитуд
определятся с точностью до множителя. Найденной таким образом – с точностью до
множителя - распределение амплитуд при собственном колебании с частотой ωk называется
собственной формой колебаний.
2.5.4 Собственные значения и собственные векторы.
Описанная выше задача о свободных колебаниях в математике называется «проблема собственных значений (чисел) и собственных векторов».
Говорят, что столбец ![]() является
собственным вектором матрицы
является
собственным вектором матрицы ![]() , соответствующим
собственному числу
, соответствующим
собственному числу ![]() , если выполняется
равенство
, если выполняется
равенство
![]() ,
,
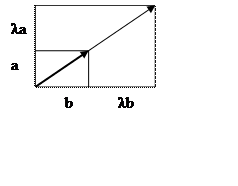 т.е. матрица
т.е. матрица ![]() переводит
вектор
переводит
вектор![]() в колинеарный ему вектор.
в колинеарный ему вектор.
Равенство можно переписать в виде однородной системы уравнений
![]() , *)
, *)
ненулевое решение которого возможно при равенстве нулю определителя матрицы
![]() .
.
Последнее уравнение представляет собой полином степени ![]() относительно
относительно ![]() и
называется характеристическим уравнением, вековым уравнением, частотным
уравнением.
и
называется характеристическим уравнением, вековым уравнением, частотным
уравнением.
Если матрица К – положительно определенная, то все ее
собственные значения![]() –
положительны, и, в таком случае, они имеют вещественные значения
–
положительны, и, в таком случае, они имеют вещественные значения ![]() .
.
Доказывается, что если исходное положение есть положение
устойчивого равновесия, то матрица ![]() =
=![]() , размером
, размером ![]() *
*![]() ,удовлетворяет приведенному выше требованию и, следовательно, динамическая
система имеет
,удовлетворяет приведенному выше требованию и, следовательно, динамическая
система имеет ![]() собственных чисел с учетом
их кратности.
собственных чисел с учетом
их кратности.
Если имеет место взаимно однозначное соответствие собственного числа и собственного вектора, то собственное число называют простым (корнем характеристического уравнения). Если корню λk соответствуют m собственных векторов (в нашей задаче – одной частоте соответствуют несколько собственных форм), то говорят о кратном корне характеристического уравнения или о корне кратности m.
- простой корень ![]()
- кратный корень 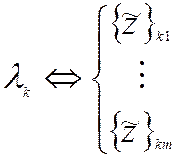 , m - кратность.
, m - кратность.
Общее количество корней равно nс учетом их кратности: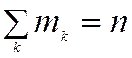 .
.
Очевидно, что при умножении любого собственного вектора на произвольное число равенство *) не нарушается.
Задание множителя определяет процедуру нормирования, которая может быть выполнена различными способами:
Часто наибольшую из компонент вектора ![]() принимают равной 1;
принимают равной 1;
Можно принять равным 1 перемещение ![]() ;
;
Часто оказывается удобным нормировать модуль вектора
(эвклидова норма) 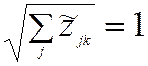 .
.
Изучение теории собственных чисел и собственных векторов представляет исключительный интерес ввиду того, что
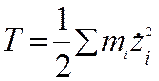 ,
, 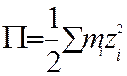 и др.) ;
и др.) ;2.5.5 Свойства собственных форм
Говорят, что векторы![]() и
и![]() ортогональны, если выполняется
соотношение
ортогональны, если выполняется
соотношение
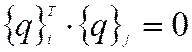 .
.
I. Свойства ортогональности собственных форм.
Для собственных форм справедливы следующие соотношения
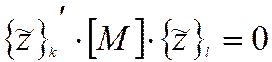 - ортогональность по
матрице*) масс;
- ортогональность по
матрице*) масс;
и
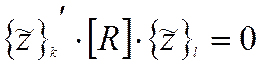 - ортогональность по
матрице жесткости.
- ортогональность по
матрице жесткости.
*) с матрицей, относительно матрицы.
II Если собственные частоты упорядочены, как положено, т.е.
![]() ,
,
то при увеличении порядкового номера собственной частоты увеличивается
количество узловых точек собственной формы, под которыми понимается
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.