




II семестр ЛЕКЦИЯ 6
Тема 4: Колебания и устойчивость нелинейных систем
4.1 О нелинейных задачах строительной механики
Задачи устойчивости – нелинейные. Обсуждая устойчивость сжатых стержней и рам, мы рассматривали линеаризованные постановки задач – устойчивость в смысле Эйлера.
Типы нелинейностей:
· Нелинейная упругость
· Упруго-пластические системы
 Геометрическая нелинейность
– большие перемещения порождают изменение геометрии системы.
Геометрическая нелинейность
– большие перемещения порождают изменение геометрии системы.А также: ползучесть, трение и др.
Задачи устойчивости относятся к классу геометрически нелинейных задач. Нелинейные постановки задач динамики и устойчивости будем рассматривать на примере фермы Мизеса.
4.2 Симметричная ферма Мизеса
· Стержни неограниченно прочные;
· Стержни линейно деформируемые;
· 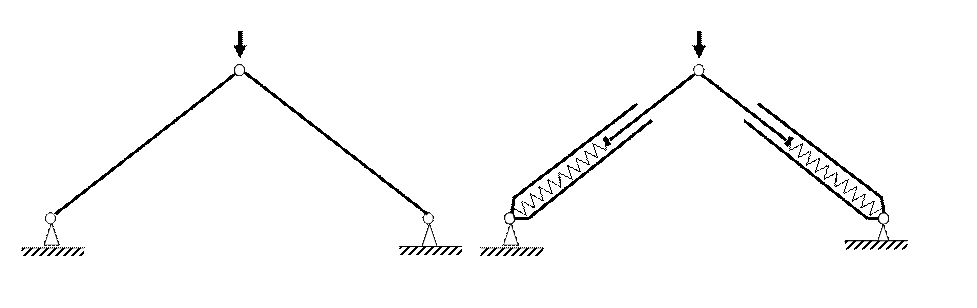 Центральный
узел может получать перемещения по вертикали и горизонтали.
Центральный
узел может получать перемещения по вертикали и горизонтали.
В связи с этими допущениями можно предположить
· Большие перемещения, влекущие изменение геометрии. Уравнения равновесия следует составлять для деформированной схемы.
· Статика: формы равновесия – симметричная и несимметричная.
· Динамика: если центральный узел несет на себе некоторую массу, то эта система с двумя степенями свободы, уравнения движения которой
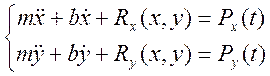
При свободных колебаниях
4.3 Симметричные формы равновесия фермы Мизеса
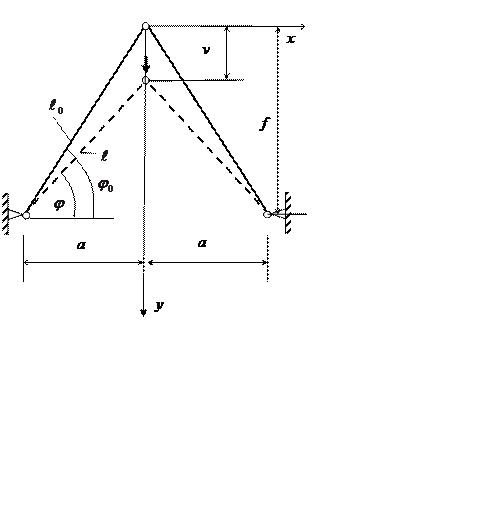
![]()
![]() Положение узла при
симметричной деформации определяется одной координатой; это может быть угол
Положение узла при
симметричной деформации определяется одной координатой; это может быть угол ![]() или текущее значение ординаты,
равной смещению (
или текущее значение ординаты,
равной смещению (![]() ).
).
Уравнение равновесия в линейной постановке:
![]() .
.
Уравнения равновесия для деформированной схемы
![]() .
.
Неизвестными в этом выражении являются и N, и φ – задача статически неопределимая. Для раскрытия статической неопределимости привлекаем геометрические и физические соотношения:
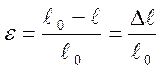 ;
;
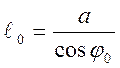 ;
; 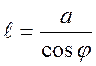 ;
;
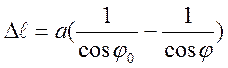 ;
;
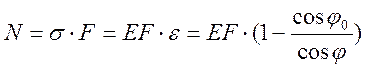 ;
;
Тогда: 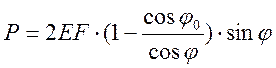 - уравнение
равновесия, содержащее одну неизвестную
- уравнение
равновесия, содержащее одну неизвестную ![]() ,
- - нелинейное относительно
,
- - нелинейное относительно ![]() уравнение.
уравнение.
Очевидно, что если известен угол ![]() ,
легко найти соответствующее ему значение нагрузки
,
легко найти соответствующее ему значение нагрузки ![]() ;
определение угла по известной силе предоставляет определенные сложности. О
методах решения нелинейных задач поговорим на следующей лекции.
;
определение угла по известной силе предоставляет определенные сложности. О
методах решения нелинейных задач поговорим на следующей лекции.
Для исследования вопросов устойчивости удобнее в
описании геометрии перейти от использования угла φ к использованию перемещения узла ![]() :
:
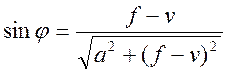 ;
; 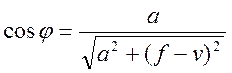 ;
;
![]() ;
; ![]() .
.
Окончательное выражение приведем без вывода:
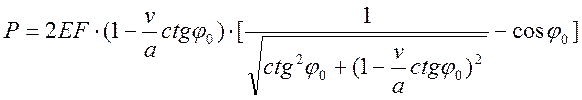 .
.
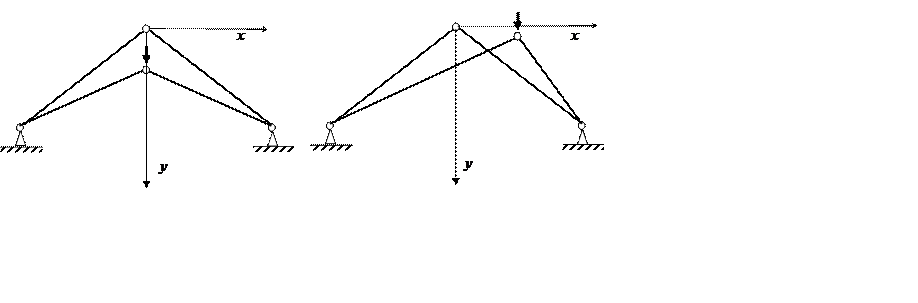
4.4 Несимметричные формы равновесия фермы Мизеса
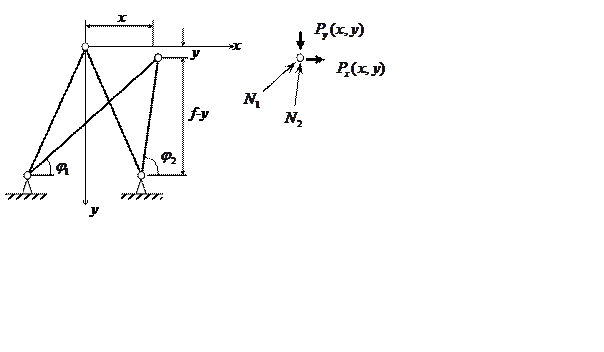
![]()
![]()
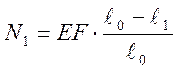
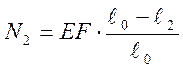
![]()
![]()
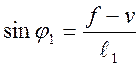 ;
; 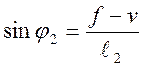 ;
; 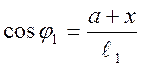 ;
;
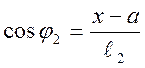
Приведенные выражения свидетельствуют о том, что ![]() и
и ![]() представляют
собой нелинейные функции от координат х
и у.
представляют
собой нелинейные функции от координат х
и у.
4.5 Устойчивость форм равновесия фермы Мизеса
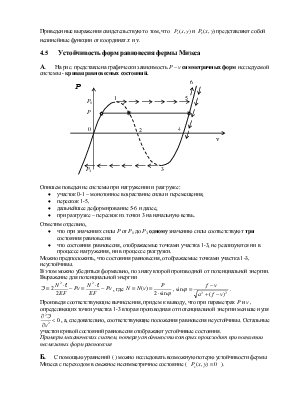
А. На рис. представлена графически зависимость Р – v симметричных форм исследуемой системы - кривая равновесных состояний.
 Опишем
поведение системы при нагружении и разгрузке:
Опишем
поведение системы при нагружении и разгрузке:
Отметим отдельно,
Можно предположить, что состояния равновесия, отображаемые точками участка 1-3, неустойчивы.
В этом можно убедиться формально, по знаку второй производной от потенциальной энергии. Выражение для потенциальной энергии
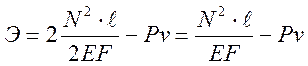 , где
, где 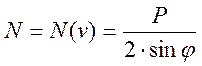 ,
, 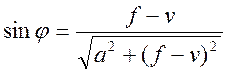 .
.
Произведя соответствующие вычисления, придем к выводу, что
при параметрах P и v , определяющих точки участка 1-3 вторая производная от
потенциальной энергии меньше нуля 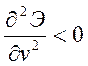 , а,
следовательно, соответствующие положения равновесия неустойчивы. Остальные
участки кривой состояний равновесия отображают устойчивые состояния.
, а,
следовательно, соответствующие положения равновесия неустойчивы. Остальные
участки кривой состояний равновесия отображают устойчивые состояния.
Примеры механических систем, потеря устойчивости которых происходит при появлении несмежных форм равновесия
Б. С
помощью уравнений ( ) можно исследовать возможную потерю устойчивости фермы
Мизеса с переходом в смежное несимметричное состояние ( ![]() ).
).
Такой анализ приведен в книге В.И. Феодосьева
«Избранные задачи и вопросы по сопротивлению материалов». Им было установлено,
что обсуждаемый тип потери устойчивости возможен, но только для относительно
«высоких» ферм ![]() .
.
4.6 Понятие о секущей и касательной жесткостях.
|
Линейная задача |
Нелинейная задача |
|
|
Вводится понятие «касательная жесткость»:
|
4.7 Касательная жесткость при симметричной деформации фермы Мизеса
|
Линейная задача:
|
|
Нелинейная задача: В это формуле переменная
Вложенная функция: Производная от вложенной функции:
При
|
Матрица касательной жесткости в состоянии k при несимметричной деформации симметричной фермы имеет вид:
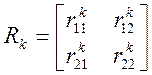 ; где
; где 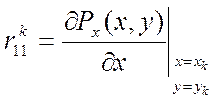 ,
, 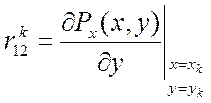 и
т.п..
и
т.п..
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.