Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров
Курсовой проект на тему:
« Синтез цифровой системы автоматического управления»
Проверил:
Выполнил: студент группы 534
.
2007
|
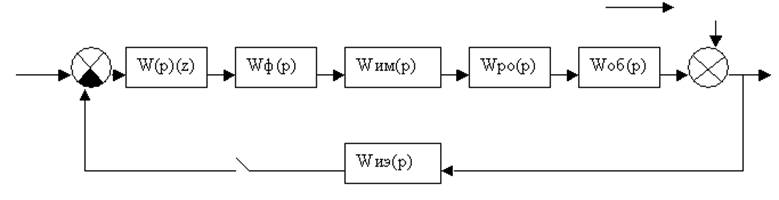
Исходные данные:
Где, К- коэффициент передачи
τ - время запаздывания
Задана передаточная функция объекта управления вида:
Wp(p)=K1+K2/p
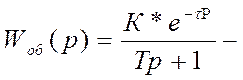 передаточная функция объекта регулирования
передаточная функция объекта регулирования
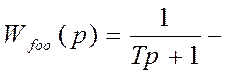 передаточная функция объекта по каналу возмущения, где T=Tf
передаточная функция объекта по каналу возмущения, где T=Tf
Принимаем:
Wим(p) = Wиэ(p) = Wро(p) = 1- передаточные функции исполнительного механизма, регулирующего органа, измерительного элемента соответственно.
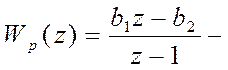 передаточная функция цифрового регулятора
передаточная функция цифрового регулятора
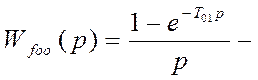 передаточная функция фиксатора
передаточная функция фиксатора
T01 –период дискретности управления
Расчет цифровой системы автоматического управления, которая удовлетворяет следующим требованиям:
1. статическая ошибка должна быть равна нулю
2. время переходного процесса должно быть минимально
3. перерегулирование не должно превышать 20%
Состав курсовой работы:
1. Выбор и обоснование закона регулирования
2. Выбор настроек регулятора, обеспечивающих выполнение заданных к переходному процессу требований
3. Расчет переходного процесса по управляющему воздействию
4. Расчет переходного процесса по возмущающему воздействию
5. Анализ полученных результатов
В качестве закона управления выбираем ПИ- закон. При правильном выборе настроек этот закон может облегчить выполнение требований к переходному процессу.
Задача выбора настроек регулятора состоит в том, чтобы в заданной системе регулирования выбрать и установить настроечные параметры регулятора, обеспечивающие протекание переходного процесса, удовлетворяющее предъявляемым к нему требованиям.
Первое требование, предъявляемое к АСР, является условие минимального времени переходного процесса регулирования, что возможно при высокой интенсивности затухания переходного режима.
Конкретизируем меру интенсивности затухания процесса регулирования. Наложим на корни Pk характеристического дифференциального линейного уравнения ограничение следующего вида:
Pk = -mw + jw. Этому
корню соответствует колебательная составляющая переходного процесса вида: Xk = A![]()
При wt = Rπ – максимум, а амплитуда колебаний Xk:
![]()
При wt i+2 = Rπ + 2π –
это максимум того же знака, что и при ti, амплитуда колебаний: ![]()
Степенью затухания (степенью колебательности) φ называется отношение разности двух соседних амплитуд, наиболее слабо затухающей составляющей переходного процесса к первой из соседних амплитуд:
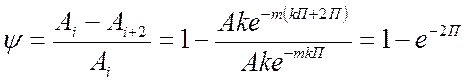
Степенью затухания
рассматриваемой составляющей процесса определяется значением ![]() , если этот корень
характеристического
, если этот корень
характеристического

![]() уравнения системы будет лежать в плоскости комплексной переменной на
уравнения системы будет лежать в плоскости комплексной переменной на

![]() линии АВ.
линии АВ.
Частотные выражения передаточной функции W(p) звеньев или системы управления, для которых p находится на линии АОВ, называется расширенные АФЧХ и обозначается W(m, w).
Наложением на корни Pk ограничение вида ![]() поставлено условие, чтобы корни
характеристического уравнения системы регулирования лежали внутри контура АОВ.
Тогда совокупность настроечных параметров регулятора b1 и b2, соответствующих контуру АОВ
образует линию равного затухания.
поставлено условие, чтобы корни
характеристического уравнения системы регулирования лежали внутри контура АОВ.
Тогда совокупность настроечных параметров регулятора b1 и b2, соответствующих контуру АОВ
образует линию равного затухания.
Соответствие настроек
регулятора заданному значению степени затухания φ, является первым условием для
определения b1 и b2. Вторым условием выполнения
соотношения является: ![]()
Это соотношение выражает связь передаточной функции объекта и регулятора в замкнутой АСР при отсутствии внешних возмущений; и является характеристическим уравнением замкнутой системы, состоящей из объекта и регулятора.
Уравнение объекта:
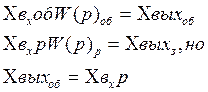 при единичной обратной
связи
при единичной обратной
связи
Следует: ![]()
![]()
![]()
![]()
![]()
При подстановке Р = -mw + jw получаем ![]()
Рассмотренные АФЧХ объекта и регулятора получаем подстановкой ограничения на корни Р = -mw + jw в уравнение передаточных функций объекта и регулятора в показательную форму записи:
![]()
![]()
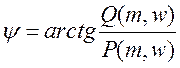
У объекта: ![]()
![]()
У регулятора: ![]()
![]()
Параметры объекта ![]() заранее известны, а выбрав
заранее известны, а выбрав ![]() определяем соответствующую m.
определяем соответствующую m.
Параметры регулятора ![]() необходимо определить из условия
необходимо определить из условия
![]()
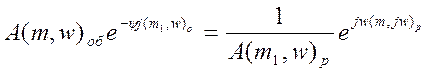
Это равенство двух
комплексных чисел возможно в том случае, если обратные модули векторов, а
аргументы отличаются на 2πn
(причем n = 0), т.е. 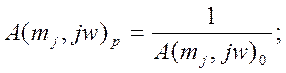
![]()
Запишем эти соотношения в следующей форме:
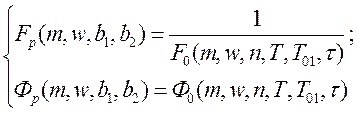
Решим систему уравнений с двумя неизвестными, в качестве которых выбираем ![]()
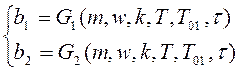
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.