Синтез цифровой системы автоматического управления. Структурная схема САУ. Передаточная функция объекта регулирования, страница 3

В данном случае, определение оптимальных настроек регулятора методом построения линии равной границе колебательности. После нахождения линии равного затухания необходимо еще определить опытным путем такиенастройки,  при которых переходный процесс полностью удовлетворяем предъявляемых к нему требований, например наименьшее время протекания переходного режима.

Поэтому возможно более эффективным и удобным был бы расчет  и  путем подбора внутри области устойчивости замкнутой системы, по виду переходных процессов, т.к. при использовании z – преобразования возможно построение переходных процессов при помощи разностных уравнений, что достаточно удобно. При подборе  и  стремятся обеспечить заданную степень затухания и минимальную площадь под графиком переходного процесса, а значит и наименьшее время его протекания.

Построить область устойчивости цифровой автоматической системы для облегчения поиска оптимальных значений коэффициентов динамической настройки  и  цифрового регулятора, можно с помощью дискретной передаточной функции W(z) разомкнутой ЦАС. Для этого используется характеристическое уравнение замкнутой ЦАС. D (z) = 1+W (z) = 0.

Апериодическая граница устойчивости L ЦАС может быть получена из характеристического уравнения при z =1, что соответствует значению относительной частоты входной синусоидальной последовательности.

Для получения границы колебательности, значения границы устойчивости ЦАС подставляют в характеристическое уравнение значения:

D (jw)= U (w)+jV (w)=i и U (w)=i, V (w)=i

Из этого находят зависимости для расчета коэффициентов динамической настройки ЦАС  и .

Расчёт переходного процесса в замкнутой ЦАС при изменении задающего воздействия.

Для расчёта переходного процесса  в замкнутой ЦАС при изменении задающего воздействия можно записать:

 где передаточная функция замкнутой ЦАС управления равна:

передаточная функция разомкнутой ЦАС управления

В нашей системе она равна произведению непрерывной части и дискретной части: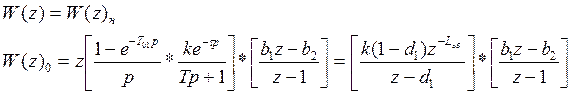

L_об = τ/T₀₁; d₁ = e^-T01/T,

T₀₁ – период дискретности

Тогда получим:

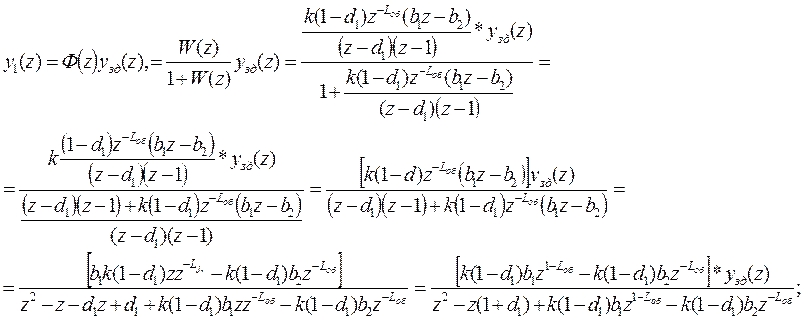
Имеем следующие исходные данные:

К = 2    τ = 10    Т = 50

Т₀₁ = Т/20 = 50/20 = 2,5;   L_об = τ / Т₀₁ =10 /2,5 =4;

d₁ = e ^-Т01/T = e ^–0.05 = 0.92

К(1- d₁) =2*(1 – 0,92) = 0,16

Подставляем значения исходных данных в уравнение:

Согласно теории смещения z – преобразования в нашем случае можно записать:

Так же:

Тогда имеем:

1.) 

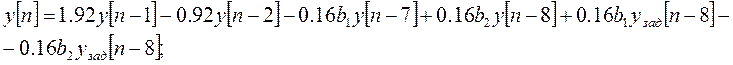
Это разностное уравнение для расчета переходного процесса в замкнутой ЦАС. Для его окончательного решения нужно задаться начальными условиями.

Пусть y_зад(t) – это мгновенное скачкообразное изменение задающего воздействия, которое математически описывается в виде:

y_зад(t)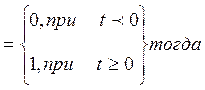

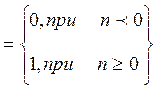
Принимаем начальные условия нулевыми:

y_зад [n] = 0, при n<0

 = 0, при n<0

Решая это разностное уравнение относительно  получим данные для построения переходного процесса в замкнутой ЦАС при изменении задающего воздействия y_зад [n].

Выбор оптимальных настроек регулятора:

Для того, чтобы найти оптимальные настройки для цифрового регулятора, необходимо найти область устойчивости системы. Ее можно найти с помощью двух кривых. Первую кривую мы получим – b1 = b2, вторая получится после решения вышеуказанного разностного уравнения: