Синтез цифровой системы автоматического управления. Структурная схема САУ. Передаточная функция объекта регулирования, страница 2

Подставляем в эти уравнения численные значения параметров объекта и величину m, получаем окончательно:

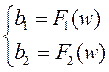
Итак, определим зависимости  для заданной АСР

1.       Передаточная функция цифрового регулятора с ПИ-законом регулирования, может быть записана в следующем виде:

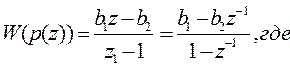
 коэффициент, характеризующий пропорциональную составляющую временной динамической характеристики цифрового ПИ – регулятора

параметр изображения решетчатой функции по времени(оригинала)

Z – преобразование связано с дискретным преобразованием Лапласа и вытекает из него.

Для решетчатых функций времени существует понятие дискретного преобразования Лапласа, определяемого формулой:

mw – абсцисса абсолютной сходимости

Если mw < ∞, то ряд определяемый функцией  сходится, и решетчатой функции соответствует некоторое изображение. Видно, что изображение решетчатой функции является функцией величины . Под

Z – преобразованием понимается изображение решетчатой функции, определяемое формулой

Z – преобразование практически совпадает с дискретным преобразованием Лапласа и отличается только аргументом соотношения изображения.

Таким образом, решетчатая функция времени (оригинал) заменяется ее изображением (Z – преобразованием).

так же может быть записано и для непрерывной функции в виде:

Эти ряды сходятся, и изображение существует, если выполняется условие, сформированное для дискретного преобразования Лапласа mw < ∞, где          mw – абсцисса абсолютной сходимости

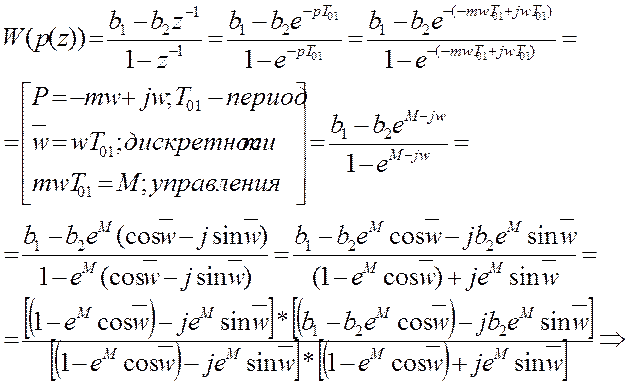
1)

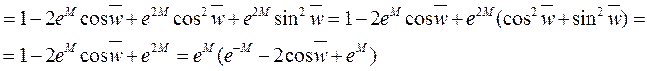
2)

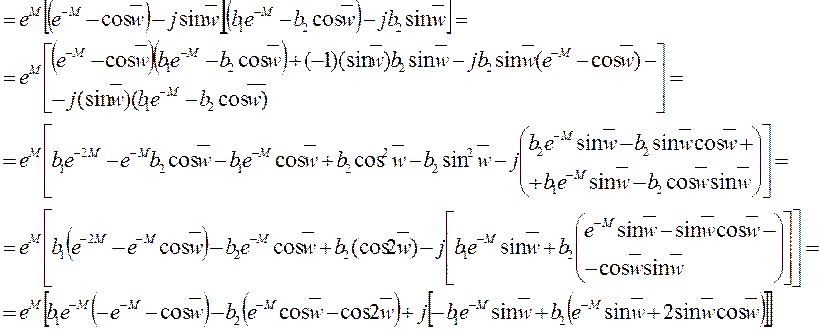
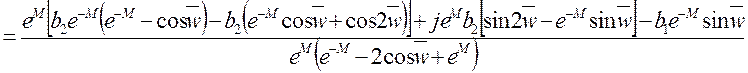
Делаем подстановки:

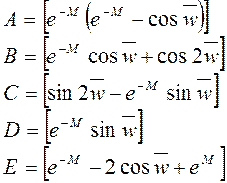
Тогда:

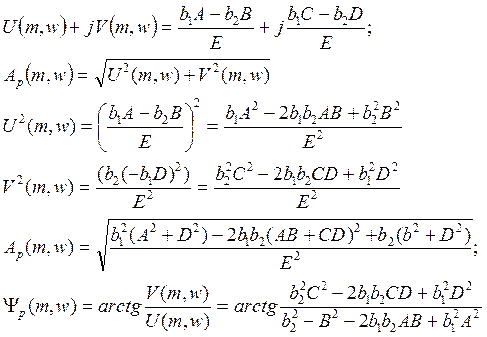
Расширенная АФЧХ регулятора в показательной форме:

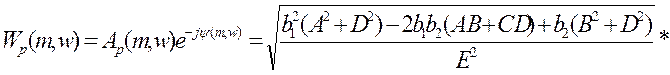
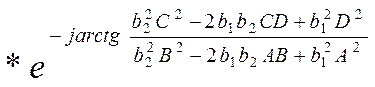
2.       Непрерывная часть данной АСР состоит из:

1.)  фиксатора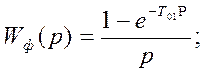

2.)  Исполнительного механизма

3.)  Регулирующего органа          

4.) Объекта управления

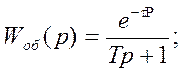
5.) Измерительного элемента

Измерительный элемент опрашивается в дискретные моменты времени t = nT₀₁. Решетчатая функция У(z) поступает в моменты t = nT₀₁ сигналы задания регулятору, например с уровня УВМ, в виде решетчатой функции G(z).Далее решетчатая функция рассогласования E(z) = G(z) – Y(z) поступает в дискретные моменты времени t = nT_01,  выходит решетчатая функция R(z), несущая в себе информацию задания команд исполнительному органу. Решетчатая функция R(z) наступает на вход фиксатора (или формирующего устройства). Задача формирующего устройства, заключается в формировании реального импульса прямоугольной, трапециидальной, треугольной и т.п. формы. В нашем случае в качестве формирующего устройства выбран фиксатор, формирующий реальные импульсы прямоугольной формы. Сигнал из фиксатора поступает в непрерывную часть системы.

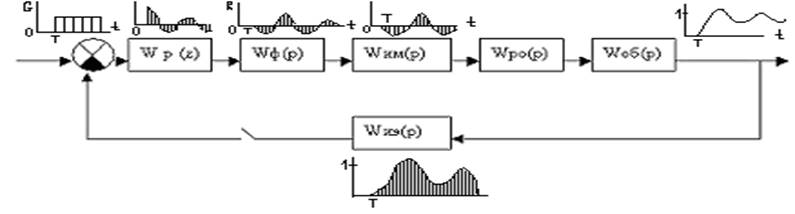Передаточная функция непрерывной части данной АСР:

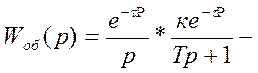в изображении по Лапласу

Непрерывная часть системы описывается изображением в форме по Лапласу, а дискретная часть описывается изображением в z- форме. Поэтому необходимо непрерывную часть описать изображением в форме z- преобразования. Это необходимо для возможности совместного использования непрерывной и дискретной частей АСР.

Поэтому:

Определение непрерывной части данной АСР, в форме расширенной АФЧХ в показательной форме.

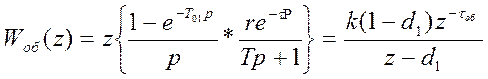
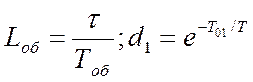
Накладываем ограничения на корни:

 и осуществляем преобразование:

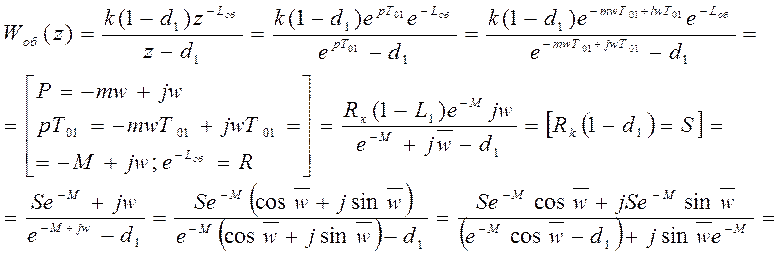
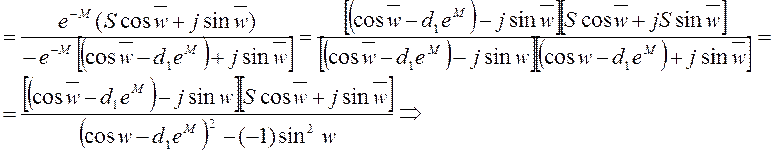
1.)

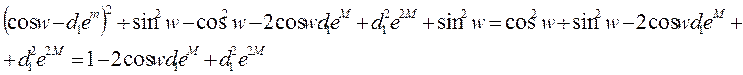
2.)

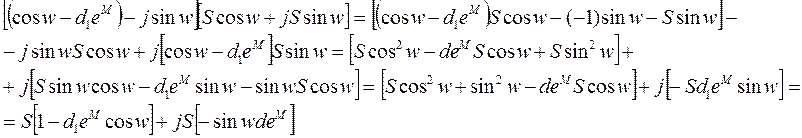
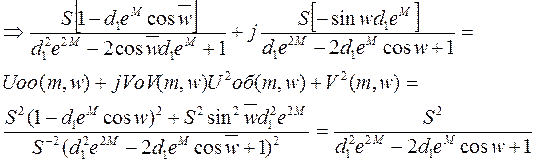
A_об(m,w)=

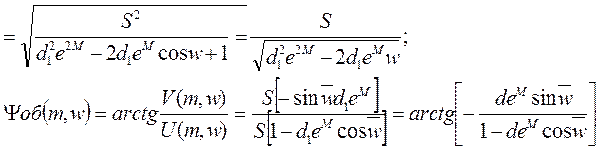
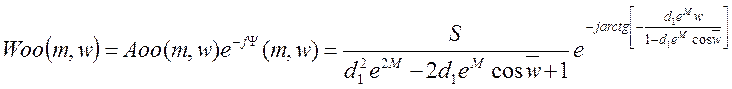
3.       Параметры настроек регулятора  необходимо определить из условий.

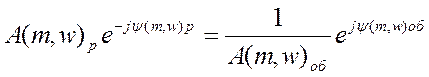
Это равенство двух комплексных чисел возможно в том случае, если равны модули векторов, а аргументы отличаются на 2πn

(примем n = 0)

т.е. 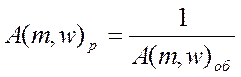 и 

1.)

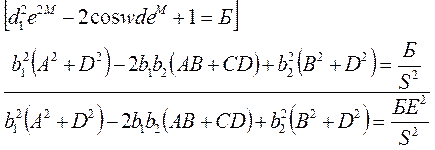
2.)

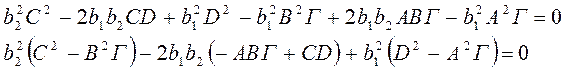
3.)

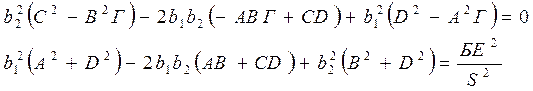
Аналитическое решение этой системы уравнений относительно  найти крайне трудно, поэтому решение можно найти только с помощью численного метода

Построение численного метода.

Построение численного метода требует дополнительного изучения, исследования, т.к. параметры A,В,C,D,E,Б,T и др. являются             функциями m и w.