




II семестр ЛЕКЦИЯ 4
2.2 Решение уравнения устойчивости центрально сжатого стержня
Итак, на прошлой лекции получено уравнение устойчивости сжато-изогнутого стержня – дифференциальное уравнение 4-го порядка с постоянными коэффициентами
![]() (для случая
(для случая ![]() и нагрузка по торцам
и нагрузка по торцам ![]() ).
).
В случае центрального сжатия:
![]() .
.
Интеграл этого уравнения (в чем можно убедиться, подставив в уравнение):
![]()
Здесь 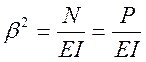 ,
, 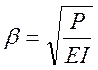 ;
;
![]() - частное решение,
зависящее от правой части, в случае qy=0
- частное решение,
зависящее от правой части, в случае qy=0
![]() ;
;
С1, С2, С3, С4 – постоянные интегрирования, определяемые из граничных условий.
2.3 Граничные условия.
Геометрические г.у. – запрет поперечных перемещений ![]() и(или)
поворота касательной
и(или)
поворота касательной![]()

![]()
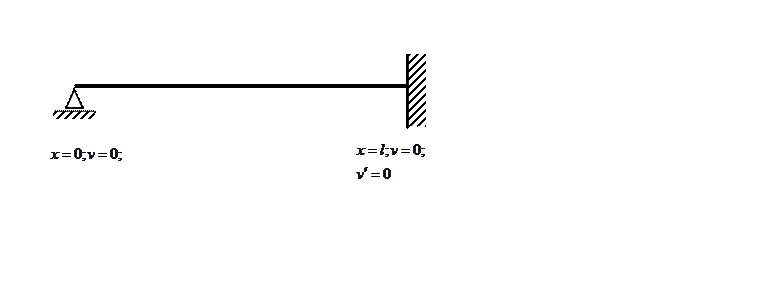
Силовые или статические г.у. – условия равновесия элемента стержня, примыкающего к торцу, в деформированном состоянии
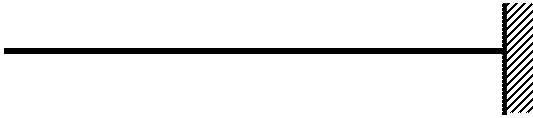
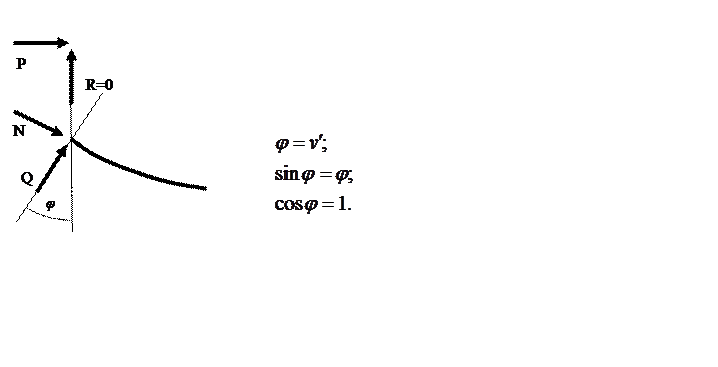
Так на свободном конце нагрузка дает условие ![]() .
.
Заменим систему торцевых сил P и R на усилия N и Q в деформированном состоянии:
![]()
Тогда ![]() ;
;
![]()
![]() .
.
Упругая опора:
![]()


![]()
![]()
2.4 Пример определения постоянных интегрирования из граничных условий:
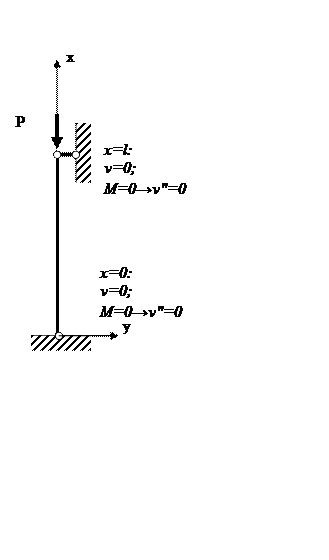
![]()
![]()
![]()
Система уравнений для определения С1, С2, С3, С4:
С2
![]()
![]()
![]()
![]()
![]()
Получена система однородных уравнений относительно![]() С1, С2,
С3, С4, допускающая два варианта решения:
С1, С2,
С3, С4, допускающая два варианта решения:
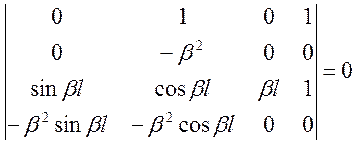 –
трансцендентное уравнение относительно
–
трансцендентное уравнение относительно ![]() .
.
Облегчим задачу получения характеристического уравнения, определив два корня из первых двух уравнений:
![]() → С2=
С4 = 0.
→ С2=
С4 = 0.
Тогда 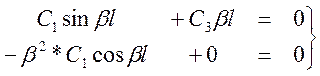 ;
;
![]() →
→ ![]() →
→ 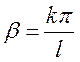 →
→ ![]() -
спектр собственных значений дифференциального уравнения;
-
спектр собственных значений дифференциального уравнения;
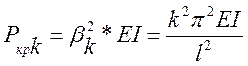 ;
; 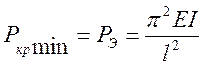 .
.
Следствием линеаризации является неопределимость перемещения.
2.5 Метод начальных параметров в задачах устойчивости (метод Клебша)
Начальные условия – частный случай граничных условий, представленных значениями геометрических и статических параметров в начале координат – начальными параметрами
Выразим постоянные интегрирования через начальные параметры, для чего
(1) ![]()
![]()
![]()
![]()
Заменим выражение поперечной силы для сечения с координатой Х (в деформированном состоянии) выражением для проекции внутренних сил на поперечное сечение в недеформированном состоянии, как это было показано при анализе силовых граничных условий:
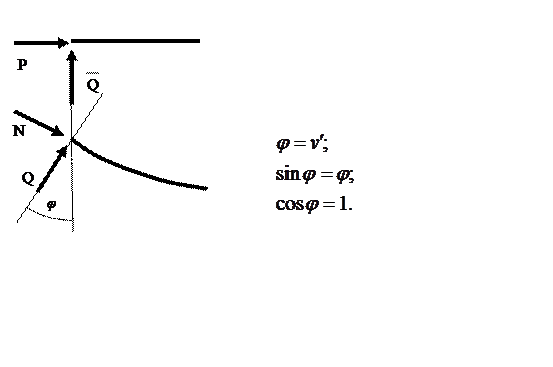



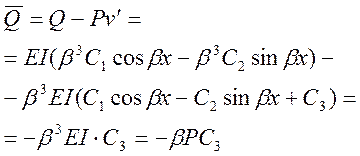
Здесь учтено, что
![]()
Система уравнений относительно С1, С2, С3, С4 получается подстановкой Х=0:
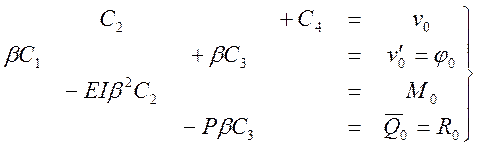
Решение системы уравнений:
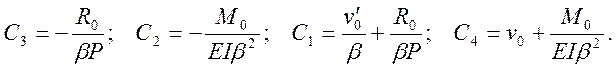
В результате получим выражения для геометрических и статических параметров стержня, подверженного действию сжимающей силы, при потере устойчивости прямолинейной формы равновесия :
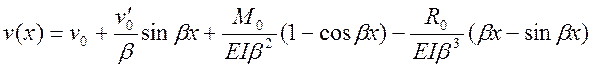
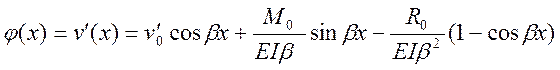
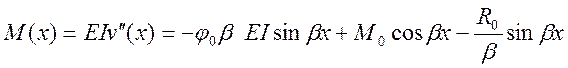
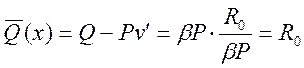 .
.
Последнее равенство является подтверждением отсутствия нагрузки, перпендикулярной недеформированной оси стержня.
Полученные выражения описывают поведение стержня в пределах одного участка, содержащего начало координат.
В случае, если при ![]() параметры
стержня меняются скачком, т.е. при
параметры
стержня меняются скачком, т.е. при ![]() получают
приращения
получают
приращения ![]() , функция перемещений также получает приращение:
, функция перемещений также получает приращение:
при ![]()
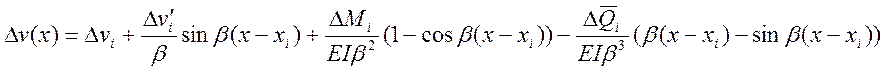 .
.
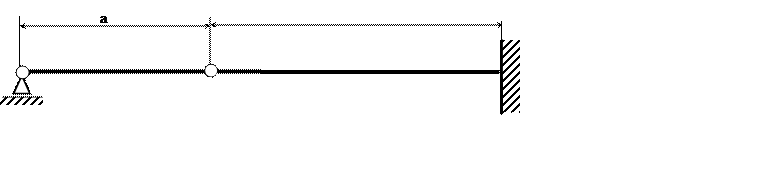
Пример:
|
|
|
|

Начальные условия и изменение
угла поворота при ![]() учтем при составлении
выражений для
учтем при составлении
выражений для 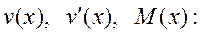
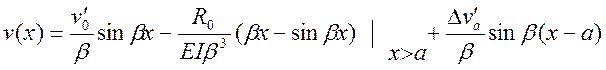
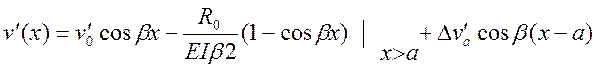
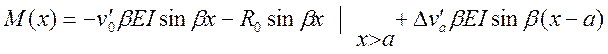
Оставшиеся условия используем для определения неизвестных ![]() :
:
![]() ;
; ![]() .
.
![]() ;
; 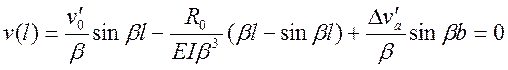 .
.
![]() ;
; 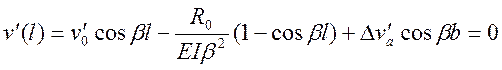 .
.
Однородная система уравнений относительно ![]() . Для получения ненулевого решения
приравниваем нулю определитель:
. Для получения ненулевого решения
приравниваем нулю определитель:
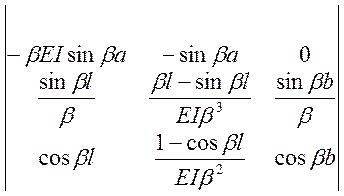 =0,
=0, ![]()
Возможны три варианта результата:



Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.