II семестр ЛЕКЦИЯ 5
Тема 3: Расчет на устойчивость плоских рам
3.1 Вводные замечания
Различают
Чисто сжатые рамы теряют устойчивость аналогично центрально сжатому стержню, т.е. в них не происходит изгиба вплоть до того момента, когда продольная сила достигнет своего критического значения, которое и является целью расчета.
Расчетная схема в виде сжато-изогнутой стержневой системы правильней отражает работу рамы, т.к. даже при отсутствии внешней нагрузки на ригели собственный вес ригелей создает деформированное состояние с изгибом элементов. Однако расчет в случае такой модели более трудоемок.
Следует иметь в виду, что сведение задачи устойчивости сжато-изогнутой рамы к задаче о чисто сжатой раме, приводит к значительному завышению критической силы.
В рамках данного курса рассматривается расчетная модель в виде чисто сжатой рамы, а именно:
Для решения используют метод сил и метод перемещений. В
первом случае перемещения ![]() определяют для
случая продольно-поперечного изгиба. Во втором – жесткость
определяют для
случая продольно-поперечного изгиба. Во втором – жесткость ![]() определяется с учетом влияния
продольной силы.
определяется с учетом влияния
продольной силы.
3.2 Метод перемещений в расчете устойчивости (чисто сжатых) рам
Неизвестные: линейные перемещения и углы поворота жестких узлов.
Основная система получается из заданной введением дополнительных связей, препятствующих независимым линейным смещениям и поворотам узлов.
Разрешающие уравнения: условия эквивалентности основной и заданной систем, т.е. условия равенства нулю усилий во введенных связях – уравнения равновесия для деформированного состояния.
Отыскиваем критическую силу в смысле Эйлера, т.е. предполагаем наличие двух смежных форм равновесия. Под смежностью понимается малость перемещений и их производных в деформированном состоянии.

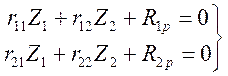
Однородная система уравнений имеет два варианта решения:
1. Тривиальное;
2.
Смежной форме равновесия соответствует решение, где хотя бы одно ![]() .
.
Ненулевое решение возможно, если определитель системы
равен нулю
![]() .
.
Сформулированное условие (характеристическое уравнение задачи) представляет собой трансцендентное уравнение относительно некоторого параметра (см. ниже), содержащего параметр нагрузки Р.
Уравнение имеет n корней (спектр решений) ![]() . Меньший корень определяет
критическую силу
. Меньший корень определяет
критическую силу ![]() .
.
Для записи уравнения устойчивости и поиска его решения
оказывается удобным, как это видно из приведенной ниже вспомогательной задачи, ввести
так называемый параметр устойчивости 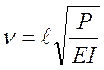 .
Параметр устойчивости с индексом 1 определяется значением наименьшего, т.е.
первого, корня уравнения
.
Параметр устойчивости с индексом 1 определяется значением наименьшего, т.е.
первого, корня уравнения 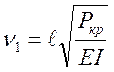 ,
,
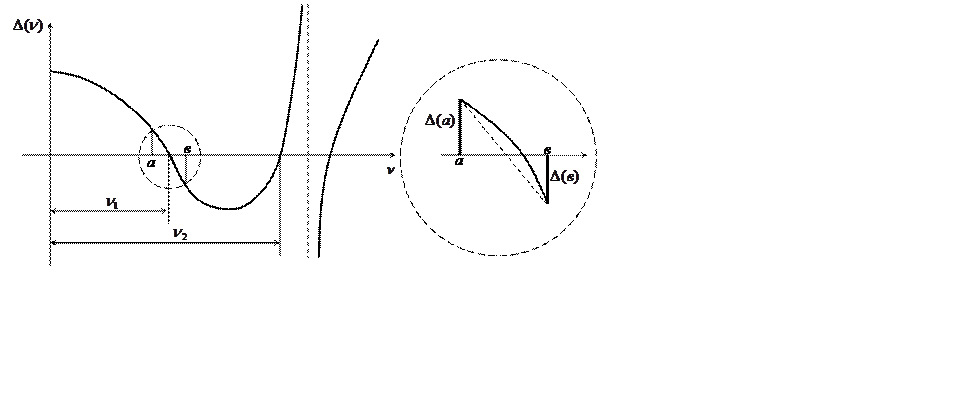
На рис. приведен вид графика зависимости определителя ![]() от параметра ν. Известно, что при
от параметра ν. Известно, что при ![]() , функция
, функция ![]() является
положительной, убывающей и имеет положительную кривизну. Это сведение полезно
при отыскании критической силы.
является
положительной, убывающей и имеет положительную кривизну. Это сведение полезно
при отыскании критической силы.
3.3 Вспомогательные задачи
|
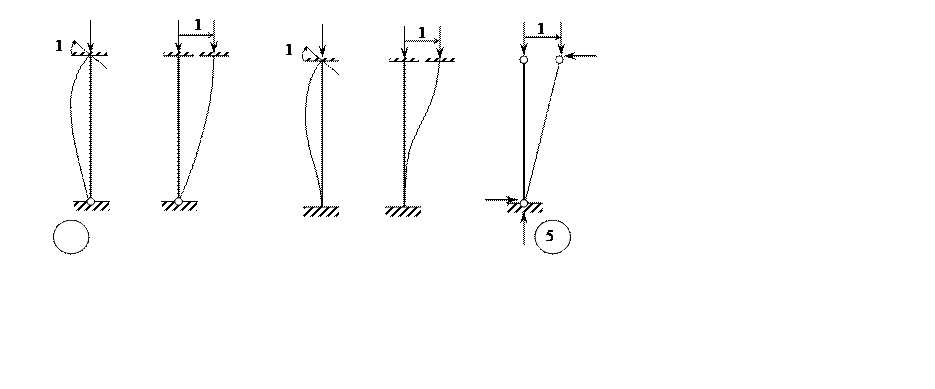
Покажем решение первой и пятой вспомогательных задач..
Задача 1
![]()
Граничные условия:
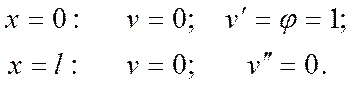 «малое», но
«единичное» перемещение.
«малое», но
«единичное» перемещение.
Два пути решения.
Путь 1:
![]()
Для определения постоянных С1, С2, С3, С4 нужно подставить это выражение в краевые условия. Получим неоднородную систему уравнений, имеющую единственное решение.
Путь 2:
Запишем решение в форме начальных параметров для стержня, имеющего один участок.
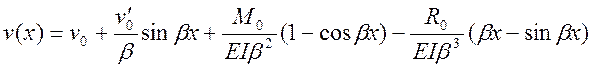 .
.
Учтем начальные условия:
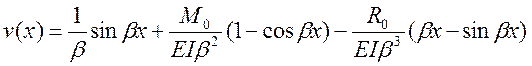
и получим выражение для второй производной, которое потребуется для удовлетворения граничным условиям на конце стержня
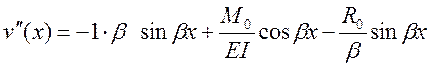 .
.
Тогда:
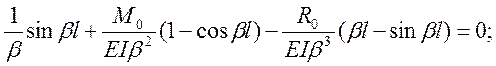 (а)
(а)
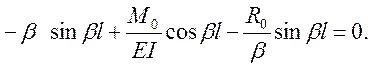 (б)
(б)
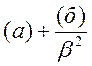 :
: 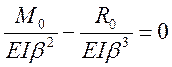 или
или 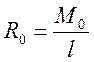 .
.
Тогда из (б):
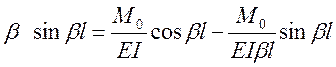 .
.
Отсюда:
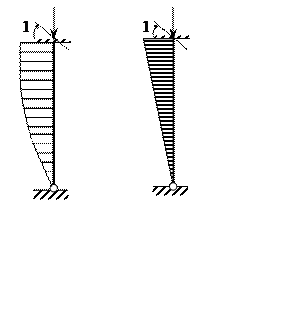
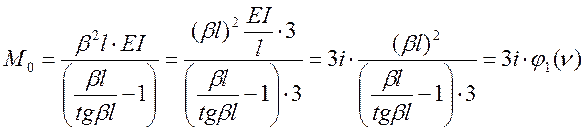
![]() .
.
Здесь:
i – погонная жесткость;
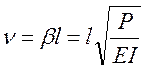 - параметр устойчивости.
- параметр устойчивости.
Заметим, что ![]() есть значение момента,
вызванного единичным поворотом заделки, при отсутствии сжимающей силы;
есть значение момента,
вызванного единичным поворотом заделки, при отсутствии сжимающей силы; ![]() - функция, понижающая жесткость в
зависимости от Р. При Р → 0 функция
- функция, понижающая жесткость в
зависимости от Р. При Р → 0 функция ![]() → 0.
→ 0.
Задача 5
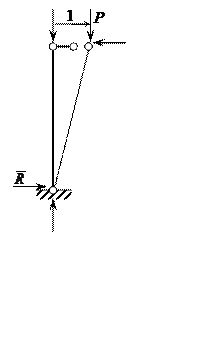
Для отклоненного положения равновесия:
![]()
![]() ;
;
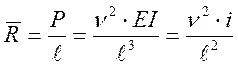
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.