Обработка исключительных ситуаций. Последовательный доступ к данным с использованием технологии BDE, страница 4

Формула для расчета:

где       x, y и z – координаты центра куба;

r – расстояние от начала координат до центра куба.

Вариант 4

Разработайте класс Новый_Треугольник на базе класса Треугольник. Добавьте в него метод, который определяет можно ли построить треугольник с заданной стороной и двумя прилежащими углами.

На основе разработанного класса решите следующую задачу: для заданных длин сторон и величин углов двух треугольников определите, существуют ли треугольники с заданными параметрами. Если такие треугольники существуют, то определите, у какого треугольника большая площадь, а у какого самый большой угол. Ответ выведите на форму.

Условие существования треугольника:

где       a и b – заданные углы, град.

Вариант 5

Разработайте класс Новый_Отрезок на базе класса Отрезок. Добавьте в него метод, определяющий, в какой четверти координатной плоскости лежит точка с заданными координатами.

На основе разработанного класса решите следующую задачу: для заданных координат концов двух отрезков определите, у какого отрезка большая длина, а какой из отрезков параллелен оси OX. Для каждого из концов отрезка определите номер четверти, в которой он лежит. Ответ выведите на форму.

Условия принадлежности точки с координатами (x, y) четверти координатной плоскости:

Вариант 6

Разработайте класс Новый_Треугольник на базе класса Треугольник. Добавьте в него метод вычисления периметра треугольника.

На основе разработанного класса решите следующую задачу: для заданных координат вершин двух треугольников определите, у какого треугольника большая площадь, у какого – самая большая длина стороны, а у какого треугольника самый большой периметр. Ответ выведите на форму.

Вариант 7

Разработайте класс Новая_Окружность на базе класса Окружность. Добавьте в него два свойства, обеспечивающие доступ к полям, которые определяют координаты центра окружности, и метод вычисления расстояния от центра окружности до начала координат.

На основе разработанного класса решите следующую задачу: для заданных диаметров двух окружностей определите, у какого круга большая площадь, насколько длина одной окружности отличается от другой и центр какой окружности ближе к началу координат. Ответ выведите на форму.

Формулы для расчета:

где       z – расстояние от центра окружности с координатами (x, y) до начала координат.

Вариант 8

Разработайте класс Новый_Прямоугольник на базе класса Прямоугольник. Добавьте в него метод вычисления периметра прямоугольника.

На основе разработанного класса решите следующую задачу: для заданных координат вершин двух прямоугольников определите, у какого прямоугольника большая диагональ, у какого – большая площадь, а у какого больший периметр. Ответ выведите на форму.

Формула для расчета:

где       a и b – длины сторон прямоугольника;

P – периметр прямоугольника.

ЛАБОРАТОРНАЯ РАБОТА № 3. Создание и вызов динамических библиотек

Цель работы: получение навыков создания и статического вызова подпрограмм динамических библиотек при разработке проектов.

Пример выполнения работы

Задание. Требуется разработать проект в СП Delphi, который вводит два целочисленных массива, находит и выводит на форму суммы их элементов и их максимальные элементы. Проект должен использовать динамическую библиотеку, содержащую две функции. Первая функция предназначена для нахождения суммы элементов целочисленного массива. Вторая – для нахождения максимального элемента целочисленного массива.

Порядок выполнения работы

1.    Создание шаблона динамической библиотеки. Выберем из меню СП Delphi командуFile / New/ Other… . В появившемся окне NewItems на вкладке New выберем DLL Wizard и щелкнем по кнопке OK.В результате будет создан шаблон проекта новой динамической библиотеки (DLL) в окне редактора, который приведен на рис. 9. Обратим внимание на то, что проект начинается зарезервированным словом library.

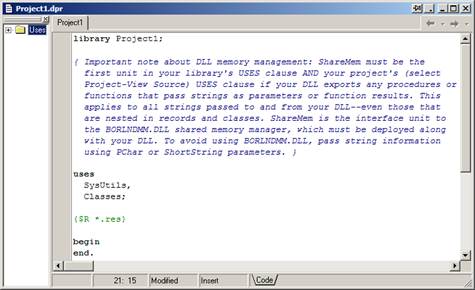Рисунок 9 – Шаблон новой динамической библиотеки