Обработка исключительных ситуаций. Последовательный доступ к данным с использованием технологии BDE, страница 3

d – длина диагонали прямоугольника;

S – площадь прямоугольника.

ЛАБОРАТОРНАЯ РАБОТА № 2. Принцип наследования классов

Цель работы: получение навыков использования принципа наследования при работе с собственным классом объектов.

Пример выполнения работы

Задание: На базе класса Прямоугольник, созданного в лабораторной работе № 1, требуется создать класс Новый_Прямоугольник с добавлением в него метод вычисления длины диагонали прямоугольника. На основе разработанного класса для заданных ширины и высоты каждого из двух прямоугольников проект в СП Delphi должен определить, у какого прямоугольника большая площадь, у какого – больший периметр, а у какого прямоугольника длинней диагональ.

Порядок выполнения работы

1.    Создание интерфейса проекта. Скопируем папку с проектом предыдущей лабораторной работы, переименуем ее и добавим объекты в окно формы. Интерфейс разрабатываемого проекта приведен на рис. 5.

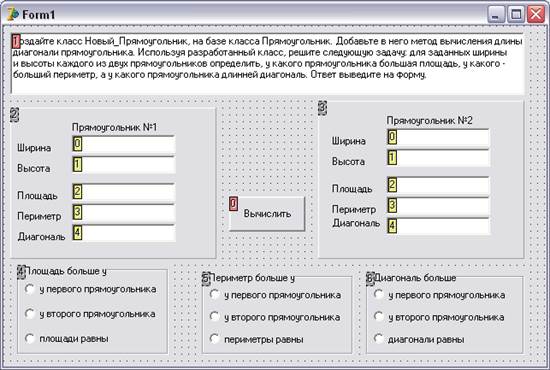
Рисунок 5 – Интерфейс проекта наследования класса

2.    Описание пользовательского класса. В конец интерфейсной части проекта допишем конструкции, определяющие создаваемый класс. На рис. 6 приведено описание класса Pramougolnik_new, объявляющее новый класс дочерним по отношению к классу Pramougolnik. В новом классе присутствует метод Diagonal, которого не было в родительском классе. Все остальные методы, равно как свойства и поля, новый метод унаследовал от класса Pramougolnik. Переменные a и b, предназначенные для работы с двумя прямо

угольниками описаны как объекты класса Pramougolnik_new.

Рисунок 6 – Описание класса Pramougolnik_new

3.    Описание нового метода. В исполняемую часть проекта добавим описание нового метода – функцию вычисления длины диагонали прямоугольника. Текст функции приведен на рис. 7.

Рисунок 7 – Описание функции для вычисления длины диагонали прямоугольника

4.    Использование созданного класса. Добавим в процедуру обработки щелчка по кнопке Вычислить необходимые операторы. Полученный текст приведен на рис. 8.

Рисунок 8 – Процедура обработки щелчка по кнопке Вычислить

Индивидуальные задания

Вариант 1

Разработайте класс Новая_Окружность на базе класса Окружность. Добавьте в него два свойства, обеспечивающие доступ к полям, которые определяют координаты центра окружности, и метод вычисления принадлежности заданной точки кругу, ограниченному окружностью.

На основе разработанного класса решите следующую задачу: для заданных радиусов двух окружностей, координат их центров и координат произвольной точки определите, у какого круга большая площадь, насколько длина одной окружности отличается от другой и какому из кругов принадлежит заданная точка. Ответ выведите на форму.

Формула для расчета:

где       z – расстояние от центра окружности с координатами (x0, y0) до точки (x1, y1).

Условие принадлежности точки (x1, y1) кругу:

где       r – радиус круга.

Вариант 2

Разработайте класс Новый_Прямоугольный_Треугольник на базе класса Прямоугольный_Треугольник. Добавьте в него метод вычисления периметра прямоугольного треугольника.

На основе разработанного класса решите следующую задачу: для заданных длин катетов двух треугольников определите, у какого треугольника большая гипотенуза, у какого – большая площадь, а у какого треугольника больший периметр. Ответ выведите на форму.

Формула для расчета:

где       a и b – длины катетов;

c – длина гипотенузы;

p – периметр прямоугольного треугольника.

Вариант 3

Разработайте класс Новый_Куб на базе класса Куб. Добавьте в него три свойства, обеспечивающие доступ к полям, которые определяют координаты центра куба в пространстве, и метод вычисления расстояния от начала координат до центра куба.

На основе разработанного класса решите следующую задачу: для заданных длин сторон и координат центров двух кубов определите, у какого куба большая поверхность, насколько объем одного куба больше другого и какой куб расположен дальше от начала координат. Ответ выведите на форму.