Обработка исключительных ситуаций. Последовательный доступ к данным с использованием технологии BDE, страница 2

Вариант 1

Разработайте класс Окружность. Свойство: радиус. Методы: длина окружности и площадь круга, ограниченного окружностью.

На основе разработанного класса решите следующую задачу: для заданных радиусов двух окружностей определите, у какого круга большая площадь и насколько длина одной окружности отличается от другой. Ответ выведите на форму.

Формулы для расчета:

где       r – радиус окружности;

C – длина окружности;

S – площадь круга.

Вариант 2

Разработайте класс Прямоугольный_Треугольник. Свойства: длины двух катетов. Методы: длина гипотенузы и площадь треугольника.

На основе разработанного класса решите следующую задачу: для заданных длин катетов двух треугольников определите, у какого треугольника большая гипотенуза, а у какого большая площадь. Ответ выведите на форму.

Формулы для расчета:

где       a и b – длины катетов;

c – длина гипотенузы;

S – площадь прямоугольного треугольника.

Вариант 3

Разработайте класс Куб. Свойство: длина стороны. Методы: площадь поверхности и объем.

На основе разработанного класса решите следующую задачу: для заданных длин сторон двух кубов определите, у какого куба большая поверхность, и насколько объем одного куба больше другого. Ответ выведите на форму.

Формулы для расчета:

где       a – длина стороны куба;

S – площадь поверхности куба;

V – объем куба.

Вариант 4

Разработайте класс Треугольник. Свойства: длина одной стороны, величины двух прилежащих к заданной стороне углов. Методы: площадь треугольника, величина третьего угла.

На основе разработанного класса решите следующую задачу: для заданных длин сторон и величин углов двух треугольников определите, у какого треугольника большая площадь, а у какого самый большой угол. Ответ выведите на форму.

Формулы для расчета:

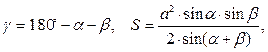
где       a – длина стороны треугольника;

a и b – углы, прилежащие к стороне a, град.;

g – третий угол треугольника, град.;

S – площадь треугольника.

Вариант 5

Разработайте класс Отрезок. Свойство: координаты концов отрезка. Методы: длина отрезка, проверка параллельности оси ОX.

На основе разработанного класса решите следующую задачу: для заданных координат концов двух отрезков определите, у какого отрезка большая длина, а какой из отрезков параллелен оси OX. Ответ выведите на форму.

Формула для расчета:

где       (x1, y1) и (x2, y2) – координаты концов отрезка;

r – длина отрезка.

Условие параллельности отрезка оси ОХ:

.

Вариант 6

Разработайте класс Треугольник. Свойства: координаты вершин треугольника. Методы: площадь треугольника, длина большей стороны.

На основе разработанного класса решите следующую задачу: для заданных координат вершин двух треугольников определите, у какого треугольника большая площадь, а у какого самая большая длина стороны. Ответ выведите на форму.

Формулы для расчета:

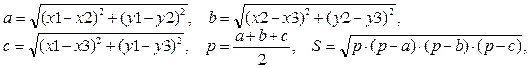
где       (x1, y1), (x2, y2) и (x3, y3) – координаты вершин треугольника;

a, b и c – длины сторон треугольника;

p – полупериметр треугольника;

S – площадь треугольника.

Вариант 7

Разработайте класс Окружность. Свойство: диаметр. Методы: длина окружности и площадь круга, ограниченного окружностью.

На основе разработанного класса решите следующую задачу: для заданных диаметров двух окружностей определите, у какого круга большая площадь и насколько длина одной окружности отличается от другой. Ответ выведите на форму.

Формулы для расчета:

где       d – диаметр окружности;

C – длина окружности;

S – площадь круга.

Вариант 8

Разработайте класс Прямоугольник. Свойства: координаты трех вершин прямоугольника. Методы: площадь прямоугольника и длина диагонали.

На основе разработанного класса решите следующую задачу: для заданных координат вершин двух прямоугольников определите, у какого прямоугольника большая диагональ, а у какого большая площадь. Ответ выведите на форму.

Формулы для расчета:

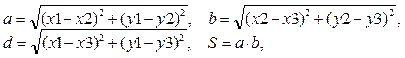
где       (x1, y1), (x2, y2) и (x3, y3) – координаты вершин прямоугольника;

a и b – длины сторон прямоугольника;