Уравнения объекта управления в векторно-матричной форме. Математическая модель системы автоматики. Входной полезный сигнал на объект управления

Министерство образования Российской Федерации

Тульский государственный университет

Кафедра «РТ и АП»

Контрольно-курсовая работа по

«Теории автоматического управления».

Выполнил студент гр. .

                                                       Научный руководитель: доцент

Тула, 2004 

Формулировка задания по контрольно-курсовой работе.

1.  По математической модели, заданной системой дифференциальных  уравнений, построить структурную схему системы.

2.  Построить граф системы.

3.  Задать переменные состояния и определить вектор входных воздействий объекта управления.

4.  Записать уравнения объекта управления в векторно-матричной форме, определить коэффициенты матриц А и В.

5.  На основе принципа регулирования по отклонению выделить в системе регулятор, элемент сравнения, датчик обратной связи и объект управления.

6.  Составить функциональную схему замкнутой системы и определить, какие принципы управления используются в исследуемой системе автоматики.

7.  Определить вид типового регулятора используемого в системе.

8.  Построить ЛАФЧХ разомкнутой системы. Определить низкочастотную, среднечастотную и высокочастотные области исследуемой системы. Оценить воспроизведение системой входного гармонического сигнала для выбранных  нами значений низкой, средней и высокой частоты  (d%).

9.  Определить частоту среза и критическую частоту системы, полосу пропускания системы, запасы устойчивости по фазе и амплитуде.

10. Определить передаточные функции разомкнутой и замкнутой системы по входному воздействию, возмущению и ошибке.

11. Рассчитать по косвенным оценкам качества предполагаемые значения времени регулирования, перерегулирования и статической ошибки в исследуемой системе (t_p, s% и  D).

12. Оценить статическую точность системы при отсутствии и действии возмущения.

13. Методом моделирования построить переходный процесс в замкнутой системе. Оценить точность (s% и   D) и  быстродействие (t_p) в исследуемой системе при отсутствии и действия возмущения. Сопоставить фактические значения  t_p, s% и   D   с результатами косвенной оценки в пункте 11 и сделать выводы.

14. Заменить исходный регулятор системы на пропорциональный с коэффициентом передачи рассчитанным из условий обеспечения устойчивости.

15. Рассчитать момент трогания системы с пропорциональным регулятором (время начала движения) при заданной величине возмущающего воздействия.

Математическая модель системы автоматики.

dl/dt = k₁×(u - a₁×l - y)

dr/dt = k₂/T×(l + k₀×g – a₂₃×z – a₁₂×y –  1/k₂×r)

dz/dt = r – a₂×z

dy/dt = k₄×z – a₃×k₄ ×y – k₃×F(t)

В математической модели используются обозначения:

u(t) – входной полезный сигнал на объект управления,

y(t) -  выходной сигнал,

F(t) – возмущающее воздействие,

K_i – коэффициенты усиления,

a_i – коэффициенты обратных связей.

Параметры математической модели:

k₀ = 0;            a₁ = 1;

k₁ = 4;            a₂ = 0.5;

k₂ = 2.5;         a₃ = 0;

k₃ = 0.1;         a₁₂ = 0;

T = 0.03;        a₂₃ = 2.

Решение

dl/dt = 4×(u - l - y)

dr/dt = 2,5/0,03×(l + 0×g – 2×z – 0×y –  1/2,5×r)

dz/dt = r – 0,5×z

dy/dt = 0,1×z – 0×0,1×y – 0,1×F(t)

 1

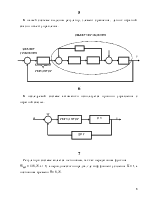
Построим структурную схему исследуемой системы. Для этого в исходных дифференциальных уравнениях объекта заменим символ дифференцирования d/dt на оператор Лапласа S, определим в каждом уравнении входные и выходные величины, составим передаточные функции блоков.

1)  sl = 4×u – 4×l - 4×y

l×(s + 4) = 4×(u – y)

a

W(s) = l/a = 4 / (s + 4) = 1 / (0,25×s + 1) – апериодическое звено 1-го порядка.

2)  sr = 83,3×l - 166,6×z – 33,32×r

r×(s + 33,32) = 83,3×(l - 2×z)

b

W(s) = r / b = 83,3 / (s + 33,32) = 2,5 / (0,03×s + 1) - апериодическое звено 1-го порядка.

3)  sz =  r – 0,5×z

z×(s + 0,5) = r

W(s) = z / r = 1 / (s+ 0,5) = 2 / (2×s + 1) - апериодическое звено 1-го порядка.

4) sy = 0,1×z – 0×0,1×y – 0,1×F(t) = 0,1×(z – F(t))

c

W(s) = y / c = 0,1 / s – интегрирующее звено.

                                   u                     a

a = u – y

y

                                                     z

b = l - 2×z

l                       b                     

                                                            F(t)

c = z – F(t)                       z                          c

z

a                    l            b                      r                     z           c                      y

y

 2

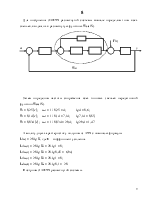
      Составим орграф Мейсона системы. В этом графе переменные состояния должны быть вершинами, а на дугах отражают операции которые нужно выполнить над одной переменной состояния, чтобы получить другую, то есть передаточную функцию W(s).

uuu                   

 3

Для представления уравнений объекта управления в переменных состояниях необходимо их переименовать в переменные x_i, где i = 1, n (n – порядок дифференциальных уравнений, описывающий объект управления). Уравнение объекта в переменных состояниях имеет вид:  x = A×x + B×U.