Введем обозначения: y = x1, z = x2, r = x3, l = x4.
Вектором входных воздействий является вектор U = (U, F) или U = (U1, U2).
4
dx1/dt = 0,1×x2 – 0,1×U2
dx2/dt = -0,5×x2 + x3
dx3/dt = -166,6×x2 – 33,32×x3 + 83,8×x4
dx4/dt = -4×x1 – 4×x4 + 4×U1
0 0,1 0 0 0 -0,1
0 -0,5 1 0 0 0
0 -166,6 -33,32 83,3 0 0
-4 0 0 -4 4 0
5
В нашей системе выделим регулятор, элемент сравнения, датчик обратной связи и объект управления.
ОБЪЕКТ УПРАВЛЕНИЯ
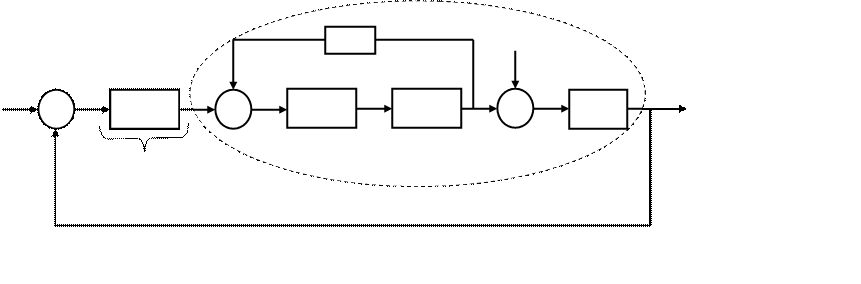
ЭЛЕМЕНТ
СРАВНЕНИЯ
y
РЕГУЛЯТОР
6
В исследуемой системе автоматики используется принцип управления с обратной связью.
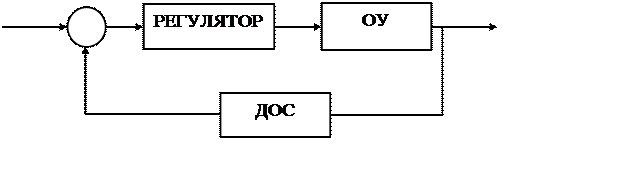ЭС
u y
7
Wрег = 1/(0,25×s + 1) апериодического порядка, где коэффициент усиления K = 1, а постоянная времени T = 0,25.
8
Для построения ЛАФЧХ разомкнутой системы вначале определим типы всех звеньев, входящих в разомкнутую функцию Wраз (S).
 |
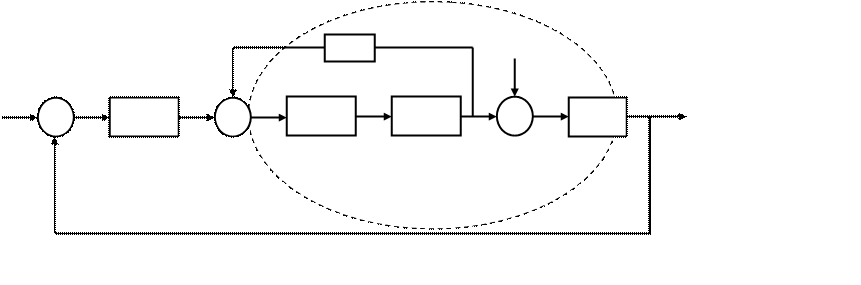F(t)
u y
Wэ1
Затем определим частоты сопряжения всех типовых звеньев передаточной функции Wраз (S).
T1 = 0,25 [c]; wc1 = 1 / 0,25 = 4; lg 4 = 0,6;
T2 = 0,14 [c]; wc2 = 1 / 0,14 = 7,14; lg 7,14 = 0,85;
T3 = 0,034 [c]; wc1 = 1 / 0,034 = 29,4; lg 29,4 = 1,47.
Амплитудную характеристику получим из АЧХ с помощью формулы
L(w) = 20×lg K, где К – коэффициент усиления.
L1(wс1) = 20×lg K1 = 20×lg 1 = 0;
L2(wс2) = 20×lg K2 = 20×lg 0,45 = -6,94;
L3(wс3) = 20×lg K3 = 20×lg 1 = 0;
L4(wс4) = 20×lg K4 = 20×lg 0,1 = -20.
Построим ЛАФЧХ разомкнутой системы.
Система устойчива, так как wкр > wср.
В нашей частотной характеристике низкочастотная область находится левее частоты среза, т.е. левее lg(wср) = -1,5.
Высокочастотная область – правее lg(wср) = -1,5.
Оценим воспроизведение системой входного гармонического сигнала для выбранного нами значения низкой частоты по формуле d% = 1 / (10Lp(wp)/20)×100%.
lg wpн = -2,5 Þ L(wpн) = 23,07 Þ d% = 1 / (1023,07 / 20) ×100% = 7%.
Оценим воспроизведение гармонического сигнала для средней частоты.
lg wpср = -1,5 Þ L(wpср) = 3,07 Þ d% = 1 / (103,07 / 20) ×100% = 70%.
Оценим воспроизведение системой входного гармонического сигнала для выбранного нами значения высокой частоты.
lg wpв = 1 Þ L(wpв) = -90,9 Þ d% = 1 / (10-90,9 / 20) ×100% = 104,5×100% = 106,5%.
9
Частота среза равна lg wср = -1,5; wср = 0,03, а критическая частота - lg wкр = 0,5; wкр = 3,16.
Запас устойчивости по фазе определяется на частоте среза, т.е.
Dj = 1800 + j (wср) = 1800 – 90,80 = 89,20.
Запас устойчивости по амплитуде определяется на критической частоте, т.е.
DА = |L (wкр) | = | L (0,5) | = 39,9.
10
Определим передаточные функции разомкнутой и замкнутой системы по входному воздействию, возмущению и ошибке.
F(t)
y
W1 = 1 / (0,25×s + 1)
Wэ1 = [0,45 / (0,14×s + 1)] × [1 / (0,03×s + 1)]
W2 = 0,1 / s
Запишем передаточную функцию разомкнутой системы:
Wраз = W1×Wэ1×W2 = [1 / (0,25×s + 1)] × [0,45 /(0,14×s +1)] × [1 / (0,03×s + 1)] × [0,1/s] =
= 0,045 / [(0,25×s + 1) × (0,14×s + 1) × (0,03×s + 1) × s].
Передаточные функции замкнутой системы
1) по полезному сигналу
Ф(s) = W1×Wэ1×W2 /
[1 + W1×Wэ1×W2] =
2) по ошибке
Фe(s) = 1 / [1+W1×Wэ1×W2] =
3) по возмущающему воздействию
ФF(s) = -W2 / [1 + W1×Wэ1×W2] =
11
Рассчитаем по косвенным оценкам качества предполагаемые значения времени регулирования, перерегулирования и статической ошибки в исследуемой системе (tp, s% и D).
Так как запас по фазе Dj (Dj = 89,20) находится в пределах 650 £ Dj £ 900, то время регулирования определяется по формуле tp = p / wср.
lg wср = -1,5 Þ wср = 10-1,5 = 0,0316 Þ tp = 3,14 / 0,0316 = 99,3 с. Перерегулирование s% = 70 - Dj = 70 – 89,2 = -19,2%.
Статическая ошибка D определяется, как D = C0 = Фe(0) = 0.
12
Оценим статическую точность системы при отсутствии и действии возмущения.
Ошибки в системах регулирования пропорциональны коэффициентам по положению С0, скорости С1, ускорению С2, первой производной по ускорению С3 и т.д. Динамическая точность в системе автоматического регулирования определяется по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.